B-Дерево: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''<math>B</math>-Дерево''' (''<math>B</math>-Tree'') - <math></math>-дерево порядка <math>m</math> есть <math>m</...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
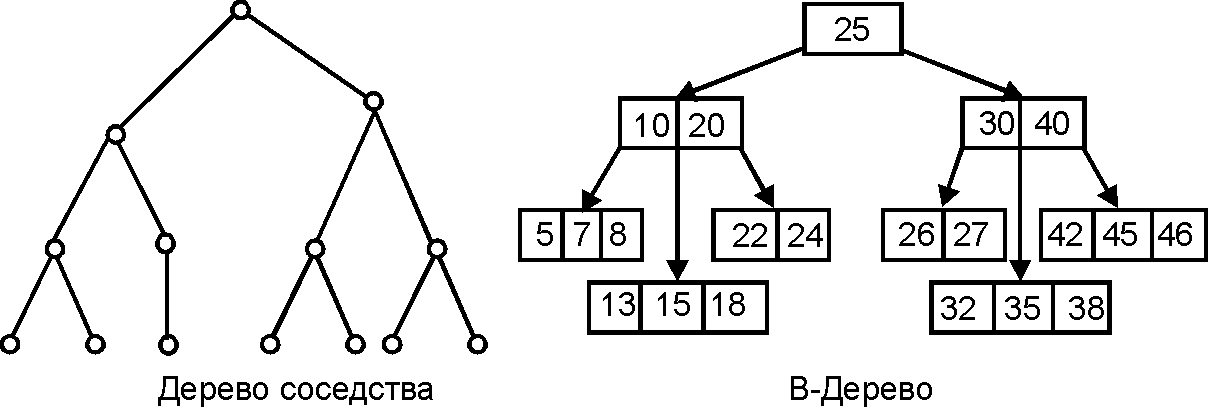
'''<math>B</math>-Дерево''' (''<math>B</math>-Tree'') | '''<math>B</math>-Дерево''' (''[[B-Tree|<math>B</math>-Tree]]'') — <math>B</math>-[[дерево]] [[порядок графа|порядка]] <math>m</math> есть <math>m</math>-арное [[выровненное дерево]], у которого каждая [[вершина]] (страница) содержит не более <math>m</math> и не менее <math>m/2</math> слов, [[корень]] имеет не менее 2 [[потомок вершины|потомков]], каждая страница либо представляет собой [[висячая вершина|висячую вершину]], либо имеет <math>k+1</math> потомков, где <math>k</math> — число слов на этой странице. <math>B</math>-дерево представляет собой структуру данных для двухуровневой памяти. | ||
<math></math>-дерево порядка <math>m</math> есть <math>m</math>-арное выровненное дерево, у которого | |||
каждая вершина (страница) содержит не более <math>m</math> и не менее <math>m/2</math> слов, | [[Файл:B-Tree.png|700px]] | ||
корень имеет не менее 2 потомков, каждая страница либо представляет | |||
собой висячую вершину, либо имеет <math>k+1</math> потомков, где <math>k</math> | |||
слов на этой странице. <math>B</math>-дерево представляет собой структуру данных | |||
для двухуровневой памяти. | |||
==Литература== | ==Литература== | ||
* Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985. | |||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
* Кнут Д. Искусство программирования для ЭВМ. — М.: Мир, 1978. — Т. 3. Сортировка и поиск. | |||
Текущая версия от 05:55, 4 февраля 2011
[math]\displaystyle{ B }[/math]-Дерево ([math]\displaystyle{ B }[/math]-Tree) — [math]\displaystyle{ B }[/math]-дерево порядка [math]\displaystyle{ m }[/math] есть [math]\displaystyle{ m }[/math]-арное выровненное дерево, у которого каждая вершина (страница) содержит не более [math]\displaystyle{ m }[/math] и не менее [math]\displaystyle{ m/2 }[/math] слов, корень имеет не менее 2 потомков, каждая страница либо представляет собой висячую вершину, либо имеет [math]\displaystyle{ k+1 }[/math] потомков, где [math]\displaystyle{ k }[/math] — число слов на этой странице. [math]\displaystyle{ B }[/math]-дерево представляет собой структуру данных для двухуровневой памяти.
Литература
- Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985.
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Кнут Д. Искусство программирования для ЭВМ. — М.: Мир, 1978. — Т. 3. Сортировка и поиск.