Двудольный граф: различия между версиями
Перейти к навигации
Перейти к поиску
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
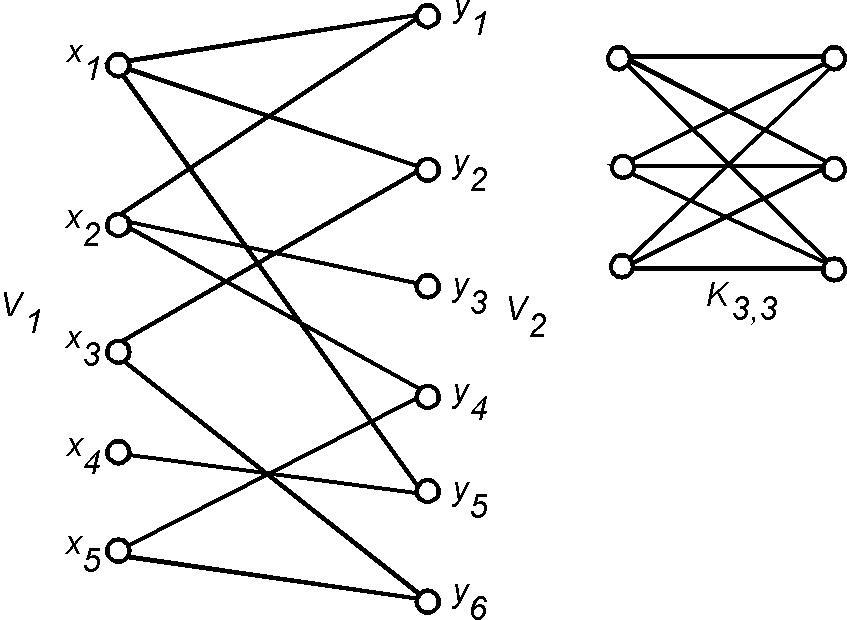
'''Двудольный граф''' (''[[Bipartite graph]]'') | '''Двудольный граф''' (''[[Bipartite graph]]'') — [[граф]], у которого существует такое разбиение | ||
множества [[вершина|вершин]] на две части (доли), что концы каждого [[ребро|ребра]] принадлежат разным долям. Если при этом любые две вершины, входящие в разные доли, [[смежные вершины|смежны]], то граф называется ''[[полный двудольный граф|полным двудольным]]''. Двудольные графы являются удобным средством графического представления отношений, а следовательно, и функций. | |||
[[Файл:Bipartite graph.png| | [[Файл:Bipartite graph.png|500px]] | ||
==См. также== | ==См. также== | ||
''[[Веер]], [[Звезда]]'' | * ''[[Веер]],'' | ||
* ''[[Звезда]].'' | |||
==Литература== | ==Литература== | ||
* Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990. | |||
Текущая версия от 06:00, 3 февраля 2011
Двудольный граф (Bipartite graph) — граф, у которого существует такое разбиение множества вершин на две части (доли), что концы каждого ребра принадлежат разным долям. Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным. Двудольные графы являются удобным средством графического представления отношений, а следовательно, и функций.
См. также
Литература
- Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.