Братское дерево: различия между версиями
Перейти к навигации
Перейти к поиску
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Братское дерево''' (''[[Brother tree]]'') | [[Файл:Brother tree.png|300px|right]] | ||
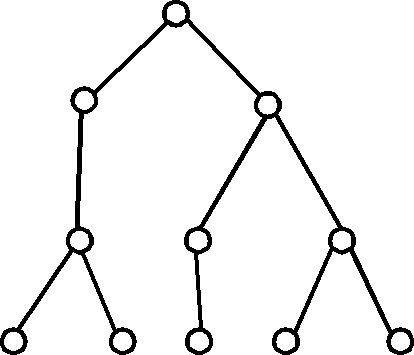
Ключи хранятся только в висячих вершинах, а во [[внутренняя вершина|внутренних]] | '''Братское дерево''' (''[[Brother tree]]'') — ''[[бинарное дерево]]'', у которого все [[висячая вершина|висячие вершины]] находятся на одном и том же [[уровень вершины|уровне]] и каждая [[вершина]] <math>x</math> с одним [[потомок вершины|потомком]] имеет ''[[брат вершины v|брата'']] <math>\beta (x)</math> с двумя потомками. | ||
Ключи хранятся только в висячих вершинах, а во [[внутренняя вершина|внутренних]] — вспомогательная информация. | |||
Другое название - [[HB- | Другое название - [[HB-Дерево|<math>HB</math>-''дерево'']]. | ||
==Литература== | ==Литература== | ||
* Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985. | |||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
Текущая версия от 09:57, 19 ноября 2010
Братское дерево (Brother tree) — бинарное дерево, у которого все висячие вершины находятся на одном и том же уровне и каждая вершина [math]\displaystyle{ x }[/math] с одним потомком имеет брата [math]\displaystyle{ \beta (x) }[/math] с двумя потомками. Ключи хранятся только в висячих вершинах, а во внутренних — вспомогательная информация. Другое название - [math]\displaystyle{ HB }[/math]-дерево.
Литература
- Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985.
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.