Базисная нумерация: различия между версиями
Перейти к навигации
Перейти к поиску
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Базисная нумерация''' (''[[Basic numbering]]'') | '''Базисная нумерация''' (''[[Basic numbering]]'') — [[нумерация вершин|''нумерация'' вершин]] [[граф|графа]], основанная на ''[[поиск в глубину|поиске в глубину]]''. К базисным нумерациям относятся ''[[прямая нумерация]]'' (или [[M-Нумерация|''<math>M</math>-нумерация'']]), | ||
''[[обратная нумерация]]'' (или [[N- | ''[[обратная нумерация]]'' (или [[N-Нумерация|''<math>N</math>-нумерация'']]). Для фиксированного | ||
обхода графа в глубину прямая нумерация определяется порядком первого попадания в вершины, а обратная | [[обход графа в глубину|обхода графа в глубину]] прямая нумерация определяется порядком первого попадания в [[вершина|вершины]], а обратная — порядком, обратным порядку возврата из вершин. | ||
[[Файл: | |||
[[Файл:Basic numbering.png|500px]] | |||
==Литература== | ==Литература== | ||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
* Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985. | |||
Текущая версия от 07:53, 19 ноября 2010
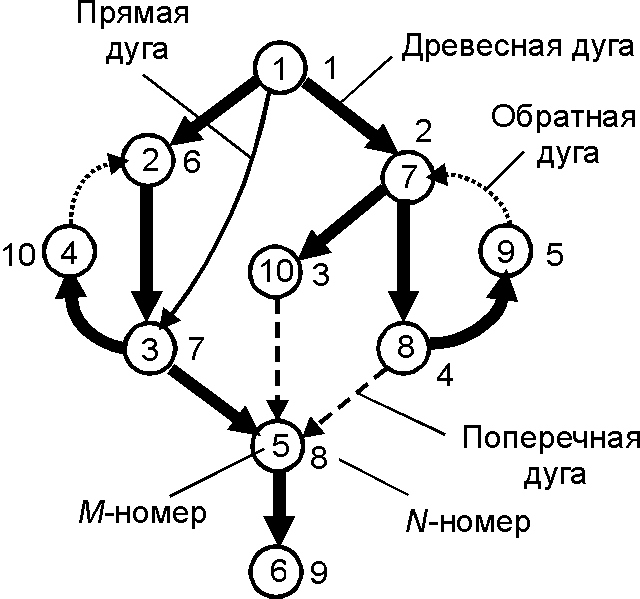
Базисная нумерация (Basic numbering) — нумерация вершин графа, основанная на поиске в глубину. К базисным нумерациям относятся прямая нумерация (или [math]\displaystyle{ M }[/math]-нумерация), обратная нумерация (или [math]\displaystyle{ N }[/math]-нумерация). Для фиксированного обхода графа в глубину прямая нумерация определяется порядком первого попадания в вершины, а обратная — порядком, обратным порядку возврата из вершин.
Литература
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985.