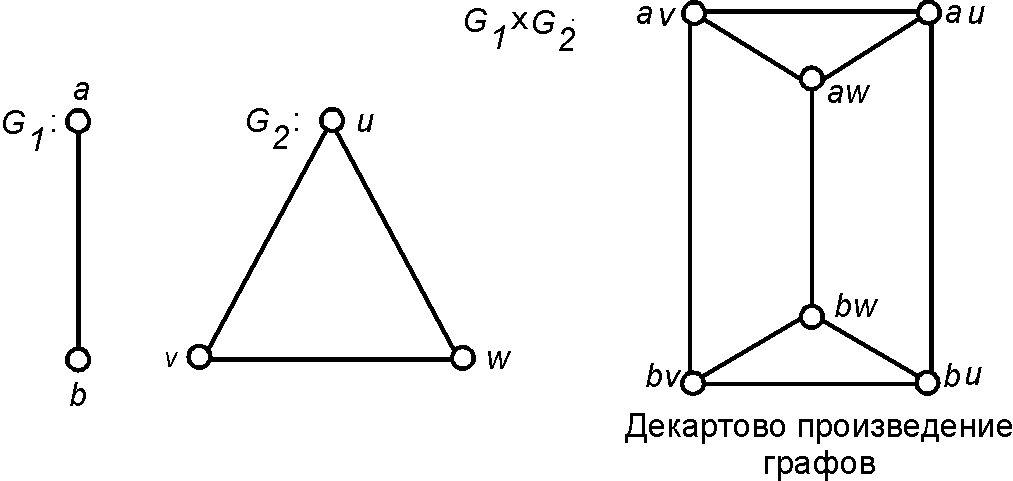Декартово произведение графов: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''Декартово произведение графов''' (''Cartesian product of graphs'') - граф <math>\pi = H_{1} \times H_{2...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
'''Декартово произведение графов''' (''Cartesian product of graphs'') - | '''Декартово произведение графов''' (''[[Cartesian product of graphs]]'') - [[граф]] <math>\pi = H_{1} \times H_{2} \times \, \ldots \, \times H_{k}</math> множество [[вершина|вершин]] которого есть декартово произведение множеств вершин графов <math>H_{i}</math>и в <math>\pi</math> существует [[ребро]] <math>(v,w)</math>, где <math>v = (v_{1}, \ldots , v_{k})</math> и <math>w = (w_{1}, \ldots , w_{k})</math> тогда и только тогда, когда существует семейство ребер | ||
граф <math>\pi = H_{1} \times H_{2} \times \, \ldots \, \times H_{k}</math> | |||
множество вершин которого есть декартово произведение множеств вершин | |||
графов <math>H_{i}</math>и в <math>\pi</math> существует ребро <math>(v,w)</math>, где <math>v = (v_{1}, | |||
\ldots , v_{k})</math>и <math>w = (w_{1}, \ldots , w_{k})</math> тогда и только | |||
тогда, когда существует семейство ребер | |||
<math>E_{1} = (v_{1},w_{1}), \; \ldots, E_{k} = (v_{k}, w_{k}), \; E_{i} | <math>E_{1} = (v_{1},w_{1}), \; \ldots, E_{k} = (v_{k}, w_{k}), \; E_{i} \subset H_{i}.</math> | ||
\subset H_{i}.</math> | |||
См. также ''Произведение графов''. | [[Файл:Cartesian product of graphs.png|700px]] | ||
==См. также== | |||
''[[Произведение графов]]''. | |||
==Литература== | ==Литература== | ||
[Оре], | [Оре], | ||
[Зыков/69]} | [Зыков/69]} | ||
Версия от 05:00, 14 октября 2009
Декартово произведение графов (Cartesian product of graphs) - граф [math]\displaystyle{ \pi = H_{1} \times H_{2} \times \, \ldots \, \times H_{k} }[/math] множество вершин которого есть декартово произведение множеств вершин графов [math]\displaystyle{ H_{i} }[/math]и в [math]\displaystyle{ \pi }[/math] существует ребро [math]\displaystyle{ (v,w) }[/math], где [math]\displaystyle{ v = (v_{1}, \ldots , v_{k}) }[/math] и [math]\displaystyle{ w = (w_{1}, \ldots , w_{k}) }[/math] тогда и только тогда, когда существует семейство ребер
[math]\displaystyle{ E_{1} = (v_{1},w_{1}), \; \ldots, E_{k} = (v_{k}, w_{k}), \; E_{i} \subset H_{i}. }[/math]
См. также
Литература
[Оре],
[Зыков/69]}