Нижняя граница для динамической связности: различия между версиями
Irina (обсуждение | вклад) |
KVN (обсуждение | вклад) |
||
| (не показаны 4 промежуточные версии 1 участника) | |||
| Строка 65: | Строка 65: | ||
На интуитивном уровне их аргументация выглядит следующим образом. В жестком экземпляре будет <math>n</math> случайных обновлений, за которыми следует один случайный запрос. Оставим <math>r \ge 2</math> для последующего определения. Идя ''назад'' по времени от запроса, можно сгруппировать обновления в экспоненциально растущие ''эпохи'': последние <math>r</math> обновлений – это эпоха 1, более ранние <math>r^2</math> обновлений – эпоха 2 и т. д. Обратите внимание, что номера эпох увеличиваются с течением времени, и всего существует <math>O(log_r \; n)</math> эпох. | На интуитивном уровне их аргументация выглядит следующим образом. В жестком экземпляре будет <math>n</math> случайных обновлений, за которыми следует один случайный запрос. Оставим <math>r \ge 2</math> для последующего определения. Идя ''назад'' по времени от запроса, можно сгруппировать обновления в экспоненциально растущие ''эпохи'': последние <math>r</math> обновлений – это эпоха 1, более ранние <math>r^2</math> обновлений – эпоха 2 и т. д. Обратите внимание, что номера эпох увеличиваются с обратным течением времени, и всего существует <math>O(log_r \; n)</math> эпох. | ||
Для некоторой эпохи <math>i</math> рассмотрим раскрытие в запросе всех обновлений, выполненных во все эпохи, отличные от <math>i</math>. Тогда запрос сводится к запросу частных сумм среди обновлений в эпоху <math>i</math>. Если запрос не касается индекса ниже минимального индекса, обновленного в эпоху <math>i</math>, ответ на запрос остается равномерно случайным, то есть имеет <math>\delta</math> бит энтропии. Более того, даже если дано, скажем, <math> | Для некоторой эпохи <math>i</math> рассмотрим раскрытие в запросе всех обновлений, выполненных во все эпохи, отличные от <math>i</math>. Тогда запрос сводится к запросу частных сумм среди обновлений в эпоху <math>i</math>. Если запрос не касается индекса ниже минимального индекса, обновленного в эпоху <math>i</math>, ответ на запрос остается равномерно случайным, то есть имеет <math>\delta</math> бит энтропии. Более того, даже если дано, скажем, <math>r^i \delta/100</math> бит информации об эпохе <math>i</math>, ответ все равно имеет в среднем <math>\Omega(\delta)</math> бит энтропии. Это происходит потому, что запрос и обновления в эпоху <math>i</math> равномерно случайны, поэтому запрос может касаться любой частной суммы этих обновлений равномерно случайным образом. Каждая из частных сумм <math>r^i</math> является независимой случайной переменной с энтропией <math>\delta</math>. | ||
| Строка 76: | Строка 76: | ||
1. Ни одна ячейка, записанная в эпохи <math>i + 1, i + 2,...</math>, не может содержать информацию об эпохе <math>i</math>, так как все они были записаны в прошлом. | 1. Ни одна ячейка, записанная в эпохи <math>i + 1, i + 2,...</math>, не может содержать информацию об эпохе <math>i</math>, так как все они были записаны в прошлом. | ||
2. В эпохи <math>1, ..., i - 1</math> было записано <math>b t_u^{\Sigma} \cdot \sum_{j = 1}^{i - 1} r^j \le b t_u^{\Sigma} \cdot 2 r^{i - 1}</math> бит. Это меньше, чем <math> | 2. В эпохи <math>1, ..., i - 1</math> было записано <math>b t_u^{\Sigma} \cdot \sum_{j = 1}^{i - 1} r^j \le b t_u^{\Sigma} \cdot 2 r^{i - 1}</math> бит. Это меньше, чем <math>r^i \delta/100</math> бит информации для <math>r > 200 t_u^{\Sigma}</math> (вспомним предположение <math>\delta = b</math>). Из вышесказанного следует, что ответ на запрос все еще имеет <math>\Omega(\delta)</math> бит энтропии. | ||
3. Поскольку значение <math>i</math> равномерно случайно среди <math>\Theta(log_r \; n)</math> эпох, запрос делает ожидаемое число <math> | 3. Поскольку значение <math>i</math> равномерно случайно среди <math>\Theta(log_r \; n)</math> эпох, запрос делает ожидаемое число <math>O(t_q^{\Sigma}/log_r \; n)</math> зондирований ячеек из эпохи <math>i</math>. Все запросы, которые не делают ни одного зондирования ячеек в эпоху <math>i</math>, получают фиксированный ответ (энтропия 0), а все остальные запросы получают ответы с энтропией менее <math>\delta</math>. Поскольку средний запрос имеет энтропию <math>\Omega(\delta)</math>, запрос должен зондировать ячейку из эпохи <math>i</math> с константной вероятностью. Это означает, что <math>t_q^{\Sigma} / log_r \; n = \Omega(1)</math>, а <math>\sum = \Omega(log_r \; n) = \Omega(lg \; n/lg \; t_u^{\Sigma})</math>. | ||
Следует оценить двойственность между техникой доказательства и естественными верхними границами, основанными на иерархии. Рассмотрим верхнюю границу, основанную на дереве степени <math>r</math>. Последние <math>r</math> случайных обновлений (эпоха 1), вероятно, равномерно распределены в массиве. Это означает, что обновления касаются разных дочерних элементов корня. Аналогично, <math>r^2</math> обновлений в эпоху 2, скорее всего, коснутся каждого узла на втором уровне дерева, и так далее. Нижняя граница свидетельствует, что запрос должен пройти путь от корня к листьям, | Следует оценить двойственность между техникой доказательства и естественными верхними границами, основанными на иерархии. Рассмотрим верхнюю границу, основанную на дереве степени <math>r</math>. Последние <math>r</math> случайных обновлений (эпоха 1), вероятно, равномерно распределены в массиве. Это означает, что обновления касаются разных дочерних элементов корня. Аналогично, <math>r^2</math> обновлений в эпоху 2, скорее всего, коснутся каждого узла на втором уровне дерева, и так далее. Нижняя граница свидетельствует, что запрос должен пройти путь от корня к листьям, зондируя узел на каждом уровне дерева (что эквивалентно одной ячейке из каждой эпохи). | ||
'''Временные иерархии''' | '''Временные иерархии''' | ||
Несмотря на значительное усовершенствование техники нижних границ, нижняя граница <math>\Omega(lg \; n/lg \; lg \; n)</math> не была улучшена до 2004 года. Тогда Петрашку и Демейн [6] | Несмотря на значительное усовершенствование техники нижних границ, нижняя граница <math>\Omega(lg \; n/lg \; lg \; n)</math> не была улучшена до 2004 года. Тогда Петрашку и Демейн [6] представили оптимальную границу <math>t_q^{\Sigma} lg(t_u^{\Sigma}/t_q^{\Sigma}) = \Omega(lg \; n)</math>, из чего следует <math>max \{ t_u^{\Sigma}, t_q^{\Sigma} \} = \Omega(lg \; n)</math>. Для простоты нижеследующее обсуждение пренебрегает этим компромиссом и просто набрасывает нижнюю границу <math>\Omega(lg \; n)</math>. | ||
| Строка 97: | Строка 97: | ||
Теперь рассмотрим два «братских» поддерева, каждое из которых содержит <math>k</math> операций. Предполагается, что <math>k/2</math> обновлений в левом поддереве и <math>k/2</math> запросов в правом поддереве будут чередоваться в пространстве индексов. Таким образом, запросы в правом поддереве запрашивают <math>\Omega(k)</math> различных частных сумм обновлений в левом поддереве. | Теперь рассмотрим два «братских» поддерева, каждое из которых содержит <math>k</math> операций. Предполагается, что <math>k/2</math> обновлений в левом поддереве и <math>k/2</math> запросов в правом поддереве будут чередоваться в пространстве индексов. Таким образом, запросы в правом поддереве запрашивают <math>\Omega(k)</math> различных частных сумм обновлений в левом поддереве. Так что правому поддереву «нужно» <math>\Omega(k \delta)</math> бит информации о левом поддереве, и эта информация может поступать только из ячеек, записанных в левом поддереве и прочитанных в правом. Отсюда следует нижняя граница в <math>\Omega(k)</math> зондов, связанных с родителем «братских» поддеревьев. Эта граница линейна по числу листьев, так что, суммируя по всему дереву, мы получаем полную нижнюю границу <math>\Omega(n \; lg \; n)</math>, или стоимость <math>\Omega(lg \; n)</math> на операцию. | ||
'''Оптимальное построение эпох''' | '''Оптимальное построение эпох''' | ||
Как ни удивительно, но Петрашку и Тарнице [7] удалось воспроизвести оптимальный компромисс теоремы 1 с минимальными изменениями рассуждений об эпохах. В старой версии этих рассуждений информация, раскрываемая эпохами <math>1, ..., i - 1</math> об эпохе <math>i</math>, ограничивалась количеством ячеек, записанных в эти эпохи. Ключевая идея заключается в том, что не менее | Как ни удивительно, но Петрашку и Тарнице [7] удалось воспроизвести оптимальный компромисс теоремы 1 с минимальными изменениями рассуждений об эпохах. В старой версии этих рассуждений информация, раскрываемая эпохами <math>1, ..., i - 1</math> об эпохе <math>i</math>, ограничивалась количеством ячеек, записанных в эти эпохи. Ключевая идея заключается в том, что не менее удачной границей является количество ячеек, прочитанных в эпохи <math>1, ..., i - 1</math> и записанных в эпоху <math>i</math>. | ||
В принципе, все операции чтения ячеек из эпохи <math>i - 1</math> могут читать данные из эпохи <math>i</math>, что делает эти две границы идентичными. Однако можно рандомизировать построение эпох, вставляя запрос после непредсказуемого количества обновлений. Такая рандомизация «сглаживает» распределение эпох, из которых считываются ячейки, то есть запрос считывает <math>O(t_q^{\Sigma}/log_r \; n)</math> ячеек из каждой эпохи, что выходит за рамки случайности в построении эпохи. Тогда <math>O(r^{i - 1})</math>обновлений в эпохи <math>1, ..., i - 1</math> читают только <math>O(r^{i-1} \cdot t_u^{\Sigma}/log_r \; n)</math> ячеек из эпохи <math>i</math>. Этой информации недостаточно, если <math>r \gg t_u^{\Sigma}/log_r \; n = \Theta(t_u^{\Sigma}/t_q^{\Sigma})</math>, из чего следует, что <math>t_q^{\Sigma} = \Omega(log_r \; n) = Omega(lg \; n/lg(t_u^{\Sigma}/t_q^{\Sigma}))</math>. | В принципе, все операции чтения ячеек из эпохи <math>i - 1</math> могут читать данные из эпохи <math>i</math>, что делает эти две границы идентичными. Однако можно рандомизировать построение эпох, вставляя запрос после непредсказуемого количества обновлений. Такая рандомизация «сглаживает» распределение эпох, из которых считываются ячейки, то есть запрос считывает <math>O(t_q^{\Sigma}/log_r \; n)</math> ячеек из каждой эпохи, что выходит за рамки случайности в построении эпохи. Тогда <math>O(r^{i - 1})</math>обновлений в эпохи <math>1, ..., i - 1</math> читают только <math>O(r^{i-1} \cdot t_u^{\Sigma}/log_r \; n)</math> ячеек из эпохи <math>i</math>. Этой информации недостаточно, если <math>r \gg t_u^{\Sigma}/log_r \; n = \Theta(t_u^{\Sigma}/t_q^{\Sigma})</math>, из чего следует, что <math>t_q^{\Sigma} = \Omega(log_r \; n) = \Omega(lg \; n/lg(t_u^{\Sigma}/t_q^{\Sigma}))</math>. | ||
| Строка 112: | Строка 112: | ||
'''Недетерминизм''' | '''Недетерминизм''' | ||
Нижние границы, описанные выше, основаны на том, что запрос '''sum''' должен выводить | Нижние границы, описанные выше, основаны на том, что запрос '''sum''' должен выводить <math>\Omega(\delta)</math> бит информации о каждом запросе. Если мы имеем дело с ''запросом о принятии решения'' для '''testsum''', то аргумент, основанный на энтропии вывода, уже не работает. | ||
Наиболее удачной идеей для запросов на принятие решений было преобразование их в запросы с небулевым результатом в расширенной модели клеточного зонда, допускающей недетерминизм. В этой модели алгоритм запроса может порождать произвольное количество вычислительных потоков. Каждый поток может | Наиболее удачной идеей для запросов на принятие решений было преобразование их в запросы с небулевым результатом в расширенной модели клеточного зонда, допускающей недетерминизм. В этой модели алгоритм запроса может порождать произвольное количество вычислительных потоков. Каждый поток может выполнить <math>t_q</math> клеточных зондирований, после чего он должен либо завершиться ответом «отказ», либо вернуть ответ на запрос. Все потоки, не завершающиеся отказом, должны возвращать один и тот же результат. В этой модели запрос с произвольным результатом эквивалентен запросу на принятие решения, поскольку можно просто недетерминистским образом угадать ответ, а затем проверить его. | ||
Исходя из вышесказанного, задача состоит в том, чтобы доказать хорошие нижние границы для | Исходя из вышесказанного, задача состоит в том, чтобы доказать хорошие нижние границы для операции '''sum''' даже в недетерминистской модели. Недетерминизм поколебал представление о том, что при анализе эпохи i имеют значение только запросы к ячейкам эпохи <math>i</math>. Проблема в том, что запрос может не знать, ''какие'' из его зондирований действительно относятся к эпохе <math>i</math>. Зонд, считывающий ячейку из предыдущей эпохи, предоставляет по крайней мере некоторую информацию об эпохе <math>i</math>: ни одно обновление в эту эпоху не решило перезаписать ячейку. Ранее это не было проблемой, поскольку целью было только исключить случай, когда в эпоху <math>i</math> существует ''ноль'' зондирований. Теперь, однако, различные потоки могут зондировать любую ячейку в памяти, и невозможно определить, какие потоки на самом деле избегают зондирования чего-либо в эпоху <math>i</math>. Другими словами, между эпохой <math>i</math> и запросом существует скрытый канал связи, в котором эпоха может использовать выбор того, какие ячейки записывать, чтобы передать информацию запросу. | ||
Существует две основные стратегии для работы с алгоритмами недетерминированных запросов. Хасфельдт и Раухе [4] приводят доказательство, основанное на некоторых интересных наблюдениях о комбинаторике недетерминированных запросов. Петрашку и Демейн [6] используют силу самого недетерминизма для вывода небольшого сертификата, исключающего бесполезные зондирования ячеек. Из последнего результата вытекает оптимальная нижняя граница | Существует две основные стратегии для работы с алгоритмами недетерминированных запросов. Хасфельдт и Раухе [4] приводят доказательство, основанное на некоторых интересных наблюдениях о комбинаторике недетерминированных запросов. Петрашку и Демейн [6] используют силу самого недетерминизма для вывода небольшого сертификата, исключающего бесполезные зондирования ячеек. Из последнего результата вытекает оптимальная нижняя граница теоремы 1 для '''testsum''' и, следовательно, логарифмическая нижняя граница для динамической связности. | ||
| Строка 134: | Строка 134: | ||
'''Сложность битового зонда''' | '''Сложность битового зонда''' | ||
Интуитивно понятно, что если размер слова равен <math>b = 1</math>, то нижняя граница связности должна быть примерно <math>\Omega(lg^2 \; n)</math>, поскольку для запроса требуется <math>\Omega(lg \; n)</math> бит из каждой эпохи. Однако исключить что-либо, кроме нулевых зондирований в эпоху, оказывается сложно по той же причине, по которой сложен недетерминированный случай. Не давая вполне удовлетворительного понимания этой проблемы, Петрашку и Тарница [7] используют большой набор трюков, чтобы продемонстрировать нижнюю границу <math>\Omega((lg \; n/lg \; lg \; n)^2)</math> для динамической связности. Более того, они рассматривают | Интуитивно понятно, что если размер слова равен <math>b = 1</math>, то нижняя граница связности должна быть примерно <math>\Omega(lg^2 \; n)</math>, поскольку для запроса требуется <math>\Omega(lg \; n)</math> бит из каждой эпохи. Однако исключить что-либо, кроме нулевых зондирований в эпоху, оказывается сложно по той же причине, по которой сложен недетерминированный случай. Не давая вполне удовлетворительного понимания этой проблемы, Петрашку и Тарница [7] используют большой набор трюков, чтобы продемонстрировать нижнюю границу <math>\Omega((lg \; n/lg \; lg \; n)^2)</math> для динамической связности. Более того, они рассматривают задачу о частных суммах в <math>\mathbb{Z}_2</math> и показывают нижнюю границу <math>\Omega(lg \; n/lg \; lg \; lg \; n)</math>, трижды логарифмически отличающуюся от верхней. | ||
== Применение == | == Применение == | ||
| Строка 163: | Строка 163: | ||
9. Thorup, M.: Near-optimal fully-dynamic graph connectivity. In: Proc. 32nd ACM Symposium on Theory of Computing (STOC), 2000, pp. 343-350 | 9. Thorup, M.: Near-optimal fully-dynamic graph connectivity. In: Proc. 32nd ACM Symposium on Theory of Computing (STOC), 2000, pp. 343-350 | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 13:14, 30 октября 2025
Ключевые слова и синонимы
Динамические деревья (Dynamic trees)
Постановка задачи
Задача о динамической связности требует поддержки структуры графа [math]\displaystyle{ G }[/math] следующими операциями:
insert(u, v): вставка неориентированного ребра (u, v) в граф;
delete(u, v): удаление ребра (u ,v) из графа;
connected(u, v): проверка, находятся ли u и v в одной и той же связной компоненте.
Пусть [math]\displaystyle{ m }[/math] – верхняя граница количества ребер в графе. В данной статье обсуждаются нижние границы клеточного зонда для этой задачи. Обозначим за [math]\displaystyle{ t_u }[/math] сложность операций вставки и удаления, а за [math]\displaystyle{ t_q }[/math] – сложность проверки.
Задача о частных суммах
Нижние границы для задачи о динамической связности тесно связаны с нижними границами для другой классической задачи – поддержки частных сумм. Формально, задача состоит в том, чтобы поддерживать массив [math]\displaystyle{ A[1..n] }[/math], выполняя следующие операции:
update(k, [math]\displaystyle{ \Delta }[/math]): обновление [math]\displaystyle{ A[k] \leftarrow \Delta }[/math];
sum(k): возвращает частную сумму [math]\displaystyle{ \sum^k_{i=1} A[i] }[/math].
testsum(k, [math]\displaystyle{ \sigma }[/math]): возвращает булево значение, указывающее, верно ли, что [math]\displaystyle{ sum(k) = \sigma }[/math].
Чтобы полностью сформулировать задачу, будем считать, что элементы [math]\displaystyle{ A[i] }[/math] берутся из произвольной группы [math]\displaystyle{ G }[/math], содержащей не менее [math]\displaystyle{ 2^{\delta} }[/math] элементов. В модели клеточного зонда с b-битными ячейками (клетками) обозначим за [math]\displaystyle{ t_u^{\Sigma} }[/math] сложность обновления (update), а за [math]\displaystyle{ t_q^{\Sigma} }[/math] – сложность проверки (testsum), которая также является нижней границей sum.
Компромисс между [math]\displaystyle{ t_u^{\Sigma} }[/math] и [math]\displaystyle{ t_q^{\Sigma} }[/math] хорошо изучен для всех значений [math]\displaystyle{ b }[/math] и [math]\displaystyle{ \delta }[/math]. Далее будут рассматриваться только нижние границы при стандартных предположениях, что [math]\displaystyle{ b = \Omega(lg \; n) }[/math] и [math]\displaystyle{ t_u \ge t_q }[/math]. Стандартным является предположение [math]\displaystyle{ b = \Omega(lg \; n) }[/math] для верхних границ в модели с оперативной памятью; это предположение также означает, что нижняя граница применима к машине с указателями. При этих условиях Петрашку и Демейн [6] доказали следующее утверждение:
Теорема 1. Сложность задачи о частных суммах удовлетворяет соотношению: [math]\displaystyle{ t_q^{\Sigma} \cdot lg(t_u^{\Sigma} / t_q^{\Sigma}) = \Omega(\delta/b \cdot lg \; n) }[/math].
Заметим, что это совпадает с хрестоматийной верхней границей при использовании дополненных деревьев. Можно построить сбалансированное бинарное дерево над [math]\displaystyle{ A[1], ..., A[n] }[/math] и хранить в каждом внутреннем узле сумму его поддерева. Тогда обновления и запросы затрагивают [math]\displaystyle{ O(lg \; n) }[/math] узлов (и тратят [math]\displaystyle{ O(\lceil \delta /b \rceil) }[/math] времени в каждом из них из-за размера группы). Чтобы уменьшить время запросов, можно использовать B-дерево.
Связь с динамической связностью
Теперь поясним, как из нижних границ для поддержания частных сумм следуют нижние границы для динамической связности. Рассмотрим задачу о частных суммах над группой [math]\displaystyle{ G = S_n }[/math], то есть группой перестановок на [math]\displaystyle{ n }[/math] элементах. Заметим, что [math]\displaystyle{ \delta = lg(n!) = \Omega(n \; lg \; n) }[/math]. Стандартно задается [math]\displaystyle{ b = \Theta(lg \; n) }[/math], так как это естественный размер слова, используемый в верхних границах для динамической связности. Отсюда следует, что [math]\displaystyle{ t_q^{\Sigma} lg(t_u^{\Sigma}/t_q^{\Sigma}) = \Omega(n \; lg \; n) }[/math].
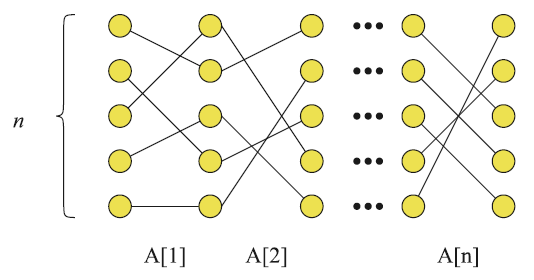
Нижняя граница вытекает из реализации операций поддержки частных сумм с помощью операций поддержки динамической связности. На рис. 1 вершины графа образуют целочисленную сетку размером [math]\displaystyle{ n \times n }[/math]. Каждая вершина инцидентна не более чем двум ребрам, одно из которых соединяется с вершиной в предыдущем столбце, а другое – с вершиной в следующем столбце. Точка [math]\displaystyle{ (x, y_1) }[/math] в сетке соединена с точкой [math]\displaystyle{ (x + 1, A[x](y_1)) }[/math], т. е. ребра между двумя смежными столбцами описывают соответствующую перестановку из вектора частных сумм.
Чтобы реализовать операцию update(x, [math]\displaystyle{ \pi }[/math]), сначала удаляются все ребра между столбцами [math]\displaystyle{ x }[/math] и [math]\displaystyle{ x + 1 }[/math], а затем вставляются новые ребра согласно [math]\displaystyle{ \pi }[/math]. Это дает [math]\displaystyle{ t_u^{\Sigma} = O(2n \cdot t_u) }[/math]. Для реализации операции testsum(x, [math]\displaystyle{ \pi }[/math]) можно использовать [math]\displaystyle{ n }[/math] запросов connected между парами точек [math]\displaystyle{ (1, у) \rightsquigarrow (х + 1, \pi(у)) }[/math]. Тогда [math]\displaystyle{ t_q^{\Sigma} = O(n \cdot t_q) }[/math]. Заметим, что запрос sum не может быть реализован так же просто. Динамическая связность является основным мотивом для изучения запроса testsum.
Рисунок 1. Построение экземпляра задачи о динамической связности, имитирующего задачу о частных суммах
Нижняя граница теоремы 1 соответствует [math]\displaystyle{ nt_q \cdot lg(2nt_u/nt_q) = \Omega(n \; lg \; n) }[/math]; следовательно, [math]\displaystyle{ t_q \; lg(t_u/t_q) = \Omega(lg \; n) }[/math]. Заметим, что из этой нижней границы следует [math]\displaystyle{ max \{ t_u, t_q \} = \Omega(lg \; n) }[/math]. Лучшая известная верхняя граница (с использованием амортизации и рандомизации) равна [math]\displaystyle{ O(lg \; n(lg \; lg \; n)^3) }[/math] [9]. Известно, что для любого [math]\displaystyle{ t_u = \Omega(lg \; n(lg \; lg \; n)^3) }[/math] компромиссная нижняя граница является строгой. Отметим, что граф в нижней границе всегда является несвязным объединением путей. Из этого следует оптимальность нижних границ для двух важных частных случаев: динамических деревьев [8] и динамической связности в планарных графах [2].
Основные результаты
Представление об иерархиях
Эпохи
Для описания техник, связанных с нижними границами, сначала рассмотрим запрос sum и предположим, что [math]\displaystyle{ \delta = b }[/math]. В 1989 году Фредман и Сакс [3] положили начало изучению нижних границ динамических клеточных зондов, по сути, доказав нижнюю границу [math]\displaystyle{ t_q^{\Sigma} \; lg \; t_u^{\Sigma} = \Omega(lg \; n) }[/math]. Заметим, что это означает, что [math]\displaystyle{ max \{ t_q^{\Sigma}, t_u^{\Sigma} \} = \Omega(lg \; n/lg \; lg \; n) }[/math].
На интуитивном уровне их аргументация выглядит следующим образом. В жестком экземпляре будет [math]\displaystyle{ n }[/math] случайных обновлений, за которыми следует один случайный запрос. Оставим [math]\displaystyle{ r \ge 2 }[/math] для последующего определения. Идя назад по времени от запроса, можно сгруппировать обновления в экспоненциально растущие эпохи: последние [math]\displaystyle{ r }[/math] обновлений – это эпоха 1, более ранние [math]\displaystyle{ r^2 }[/math] обновлений – эпоха 2 и т. д. Обратите внимание, что номера эпох увеличиваются с обратным течением времени, и всего существует [math]\displaystyle{ O(log_r \; n) }[/math] эпох.
Для некоторой эпохи [math]\displaystyle{ i }[/math] рассмотрим раскрытие в запросе всех обновлений, выполненных во все эпохи, отличные от [math]\displaystyle{ i }[/math]. Тогда запрос сводится к запросу частных сумм среди обновлений в эпоху [math]\displaystyle{ i }[/math]. Если запрос не касается индекса ниже минимального индекса, обновленного в эпоху [math]\displaystyle{ i }[/math], ответ на запрос остается равномерно случайным, то есть имеет [math]\displaystyle{ \delta }[/math] бит энтропии. Более того, даже если дано, скажем, [math]\displaystyle{ r^i \delta/100 }[/math] бит информации об эпохе [math]\displaystyle{ i }[/math], ответ все равно имеет в среднем [math]\displaystyle{ \Omega(\delta) }[/math] бит энтропии. Это происходит потому, что запрос и обновления в эпоху [math]\displaystyle{ i }[/math] равномерно случайны, поэтому запрос может касаться любой частной суммы этих обновлений равномерно случайным образом. Каждая из частных сумм [math]\displaystyle{ r^i }[/math] является независимой случайной переменной с энтропией [math]\displaystyle{ \delta }[/math].
Теперь можно поинтересоваться, сколько информации доступно для запроса. Пусть в момент запроса каждая ячейка связана с эпохой, в которую она была записана в последний раз. Выбрав эпоху [math]\displaystyle{ i }[/math] равномерно случайным образом, можно привести следующие интуитивные соображения:
1. Ни одна ячейка, записанная в эпохи [math]\displaystyle{ i + 1, i + 2,... }[/math], не может содержать информацию об эпохе [math]\displaystyle{ i }[/math], так как все они были записаны в прошлом.
2. В эпохи [math]\displaystyle{ 1, ..., i - 1 }[/math] было записано [math]\displaystyle{ b t_u^{\Sigma} \cdot \sum_{j = 1}^{i - 1} r^j \le b t_u^{\Sigma} \cdot 2 r^{i - 1} }[/math] бит. Это меньше, чем [math]\displaystyle{ r^i \delta/100 }[/math] бит информации для [math]\displaystyle{ r \gt 200 t_u^{\Sigma} }[/math] (вспомним предположение [math]\displaystyle{ \delta = b }[/math]). Из вышесказанного следует, что ответ на запрос все еще имеет [math]\displaystyle{ \Omega(\delta) }[/math] бит энтропии.
3. Поскольку значение [math]\displaystyle{ i }[/math] равномерно случайно среди [math]\displaystyle{ \Theta(log_r \; n) }[/math] эпох, запрос делает ожидаемое число [math]\displaystyle{ O(t_q^{\Sigma}/log_r \; n) }[/math] зондирований ячеек из эпохи [math]\displaystyle{ i }[/math]. Все запросы, которые не делают ни одного зондирования ячеек в эпоху [math]\displaystyle{ i }[/math], получают фиксированный ответ (энтропия 0), а все остальные запросы получают ответы с энтропией менее [math]\displaystyle{ \delta }[/math]. Поскольку средний запрос имеет энтропию [math]\displaystyle{ \Omega(\delta) }[/math], запрос должен зондировать ячейку из эпохи [math]\displaystyle{ i }[/math] с константной вероятностью. Это означает, что [math]\displaystyle{ t_q^{\Sigma} / log_r \; n = \Omega(1) }[/math], а [math]\displaystyle{ \sum = \Omega(log_r \; n) = \Omega(lg \; n/lg \; t_u^{\Sigma}) }[/math].
Следует оценить двойственность между техникой доказательства и естественными верхними границами, основанными на иерархии. Рассмотрим верхнюю границу, основанную на дереве степени [math]\displaystyle{ r }[/math]. Последние [math]\displaystyle{ r }[/math] случайных обновлений (эпоха 1), вероятно, равномерно распределены в массиве. Это означает, что обновления касаются разных дочерних элементов корня. Аналогично, [math]\displaystyle{ r^2 }[/math] обновлений в эпоху 2, скорее всего, коснутся каждого узла на втором уровне дерева, и так далее. Нижняя граница свидетельствует, что запрос должен пройти путь от корня к листьям, зондируя узел на каждом уровне дерева (что эквивалентно одной ячейке из каждой эпохи).
Временные иерархии
Несмотря на значительное усовершенствование техники нижних границ, нижняя граница [math]\displaystyle{ \Omega(lg \; n/lg \; lg \; n) }[/math] не была улучшена до 2004 года. Тогда Петрашку и Демейн [6] представили оптимальную границу [math]\displaystyle{ t_q^{\Sigma} lg(t_u^{\Sigma}/t_q^{\Sigma}) = \Omega(lg \; n) }[/math], из чего следует [math]\displaystyle{ max \{ t_u^{\Sigma}, t_q^{\Sigma} \} = \Omega(lg \; n) }[/math]. Для простоты нижеследующее обсуждение пренебрегает этим компромиссом и просто набрасывает нижнюю границу [math]\displaystyle{ \Omega(lg \; n) }[/math].
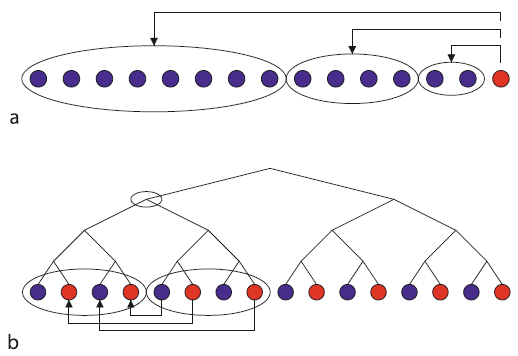
Техника подсчета Петрашку и Демейна [6] довольно сильно отличается от техники эпох; см. рис. 2. Жесткий экземпляр представляет собой последовательность из [math]\displaystyle{ n }[/math] операций, чередующих обновления и запросы. Они рассматривают сбалансированное бинарное дерево на временной оси, каждый лист которого является операцией. Теперь для каждого узла дерева авторы предлагают подсчитать количество клеточных зондирований, выполненных в правом поддереве, относительно клетки, записанной в левом поддереве. Каждое зондирование подсчитывается ровно один раз, для получения наименьшего общего предка времен чтения и записи.
Рисунок 2. Анализ зондирования клеток в методах (a), основанном на эпохах, и (b), основанном на иерархии времени
Теперь рассмотрим два «братских» поддерева, каждое из которых содержит [math]\displaystyle{ k }[/math] операций. Предполагается, что [math]\displaystyle{ k/2 }[/math] обновлений в левом поддереве и [math]\displaystyle{ k/2 }[/math] запросов в правом поддереве будут чередоваться в пространстве индексов. Таким образом, запросы в правом поддереве запрашивают [math]\displaystyle{ \Omega(k) }[/math] различных частных сумм обновлений в левом поддереве. Так что правому поддереву «нужно» [math]\displaystyle{ \Omega(k \delta) }[/math] бит информации о левом поддереве, и эта информация может поступать только из ячеек, записанных в левом поддереве и прочитанных в правом. Отсюда следует нижняя граница в [math]\displaystyle{ \Omega(k) }[/math] зондов, связанных с родителем «братских» поддеревьев. Эта граница линейна по числу листьев, так что, суммируя по всему дереву, мы получаем полную нижнюю границу [math]\displaystyle{ \Omega(n \; lg \; n) }[/math], или стоимость [math]\displaystyle{ \Omega(lg \; n) }[/math] на операцию.
Оптимальное построение эпох
Как ни удивительно, но Петрашку и Тарнице [7] удалось воспроизвести оптимальный компромисс теоремы 1 с минимальными изменениями рассуждений об эпохах. В старой версии этих рассуждений информация, раскрываемая эпохами [math]\displaystyle{ 1, ..., i - 1 }[/math] об эпохе [math]\displaystyle{ i }[/math], ограничивалась количеством ячеек, записанных в эти эпохи. Ключевая идея заключается в том, что не менее удачной границей является количество ячеек, прочитанных в эпохи [math]\displaystyle{ 1, ..., i - 1 }[/math] и записанных в эпоху [math]\displaystyle{ i }[/math].
В принципе, все операции чтения ячеек из эпохи [math]\displaystyle{ i - 1 }[/math] могут читать данные из эпохи [math]\displaystyle{ i }[/math], что делает эти две границы идентичными. Однако можно рандомизировать построение эпох, вставляя запрос после непредсказуемого количества обновлений. Такая рандомизация «сглаживает» распределение эпох, из которых считываются ячейки, то есть запрос считывает [math]\displaystyle{ O(t_q^{\Sigma}/log_r \; n) }[/math] ячеек из каждой эпохи, что выходит за рамки случайности в построении эпохи. Тогда [math]\displaystyle{ O(r^{i - 1}) }[/math]обновлений в эпохи [math]\displaystyle{ 1, ..., i - 1 }[/math] читают только [math]\displaystyle{ O(r^{i-1} \cdot t_u^{\Sigma}/log_r \; n) }[/math] ячеек из эпохи [math]\displaystyle{ i }[/math]. Этой информации недостаточно, если [math]\displaystyle{ r \gg t_u^{\Sigma}/log_r \; n = \Theta(t_u^{\Sigma}/t_q^{\Sigma}) }[/math], из чего следует, что [math]\displaystyle{ t_q^{\Sigma} = \Omega(log_r \; n) = \Omega(lg \; n/lg(t_u^{\Sigma}/t_q^{\Sigma})) }[/math].
Технические трудности
Недетерминизм
Нижние границы, описанные выше, основаны на том, что запрос sum должен выводить [math]\displaystyle{ \Omega(\delta) }[/math] бит информации о каждом запросе. Если мы имеем дело с запросом о принятии решения для testsum, то аргумент, основанный на энтропии вывода, уже не работает.
Наиболее удачной идеей для запросов на принятие решений было преобразование их в запросы с небулевым результатом в расширенной модели клеточного зонда, допускающей недетерминизм. В этой модели алгоритм запроса может порождать произвольное количество вычислительных потоков. Каждый поток может выполнить [math]\displaystyle{ t_q }[/math] клеточных зондирований, после чего он должен либо завершиться ответом «отказ», либо вернуть ответ на запрос. Все потоки, не завершающиеся отказом, должны возвращать один и тот же результат. В этой модели запрос с произвольным результатом эквивалентен запросу на принятие решения, поскольку можно просто недетерминистским образом угадать ответ, а затем проверить его.
Исходя из вышесказанного, задача состоит в том, чтобы доказать хорошие нижние границы для операции sum даже в недетерминистской модели. Недетерминизм поколебал представление о том, что при анализе эпохи i имеют значение только запросы к ячейкам эпохи [math]\displaystyle{ i }[/math]. Проблема в том, что запрос может не знать, какие из его зондирований действительно относятся к эпохе [math]\displaystyle{ i }[/math]. Зонд, считывающий ячейку из предыдущей эпохи, предоставляет по крайней мере некоторую информацию об эпохе [math]\displaystyle{ i }[/math]: ни одно обновление в эту эпоху не решило перезаписать ячейку. Ранее это не было проблемой, поскольку целью было только исключить случай, когда в эпоху [math]\displaystyle{ i }[/math] существует ноль зондирований. Теперь, однако, различные потоки могут зондировать любую ячейку в памяти, и невозможно определить, какие потоки на самом деле избегают зондирования чего-либо в эпоху [math]\displaystyle{ i }[/math]. Другими словами, между эпохой [math]\displaystyle{ i }[/math] и запросом существует скрытый канал связи, в котором эпоха может использовать выбор того, какие ячейки записывать, чтобы передать информацию запросу.
Существует две основные стратегии для работы с алгоритмами недетерминированных запросов. Хасфельдт и Раухе [4] приводят доказательство, основанное на некоторых интересных наблюдениях о комбинаторике недетерминированных запросов. Петрашку и Демейн [6] используют силу самого недетерминизма для вывода небольшого сертификата, исключающего бесполезные зондирования ячеек. Из последнего результата вытекает оптимальная нижняя граница теоремы 1 для testsum и, следовательно, логарифмическая нижняя граница для динамической связности.
Альтернативные истории
Описанная выше схема опирается на фиксацию всех обновлений в эпохи, отличные от [math]\displaystyle{ i }[/math], к среднему значению и утверждение, что ответ на запрос все равно имеет большую вариативность, зависящую от обновлений в эпоху [math]\displaystyle{ i }[/math]. Это верно для задач агрегирования, но не для задач поиска. Если искомый элемент найден с равной вероятностью в любой эпохе, то фиксация всех остальных эпох делает эпоху [math]\displaystyle{ i }[/math] нерелевантной с вероятностью [math]\displaystyle{ 1 - 1/(log_r \; n) }[/math].
Олстрап и др. [1] предложили очень интересное усовершенствование этой техники, доказав нижние границы [math]\displaystyle{ \Omega(lg \; n/ lg \; lg \; n) }[/math] для впечатляющей коллекции задач поиска. Интуитивно их идея заключается в рассмотрении [math]\displaystyle{ O(log_r \; n) }[/math] альтернативных историй обновлений, выбранных независимо друг от друга случайным образом. Эпоха [math]\displaystyle{ i }[/math] релевантна хотя бы в одной из историй с константной вероятностью. С другой стороны, даже если известно, что эпохи с 1 по [math]\displaystyle{ i - 1 }[/math] узнали об эпохе [math]\displaystyle{ i }[/math] во всех историях, ответить на случайный запрос все равно сложно.
Сложность битового зонда
Интуитивно понятно, что если размер слова равен [math]\displaystyle{ b = 1 }[/math], то нижняя граница связности должна быть примерно [math]\displaystyle{ \Omega(lg^2 \; n) }[/math], поскольку для запроса требуется [math]\displaystyle{ \Omega(lg \; n) }[/math] бит из каждой эпохи. Однако исключить что-либо, кроме нулевых зондирований в эпоху, оказывается сложно по той же причине, по которой сложен недетерминированный случай. Не давая вполне удовлетворительного понимания этой проблемы, Петрашку и Тарница [7] используют большой набор трюков, чтобы продемонстрировать нижнюю границу [math]\displaystyle{ \Omega((lg \; n/lg \; lg \; n)^2) }[/math] для динамической связности. Более того, они рассматривают задачу о частных суммах в [math]\displaystyle{ \mathbb{Z}_2 }[/math] и показывают нижнюю границу [math]\displaystyle{ \Omega(lg \; n/lg \; lg \; lg \; n) }[/math], трижды логарифмически отличающуюся от верхней.
Применение
Обсуждаемая здесь нижняя граница путем простых редукций распространяется практически на все естественные полностью динамические задачи на графах [6].
Открытые вопросы
Наиболее важной задачей будущих исследований является получение нижней границы [math]\displaystyle{ \omega(lg \; n) }[/math] на операцию для некоторой динамической структуры данных в модели клеточного зонда с размером слова [math]\displaystyle{ \Theta(lg \; n) }[/math]. Милтерсен [5] определяет набор технических условий для того, что считается решением такой задачи. В частности, задача должна быть проблемой динамической принадлежности языку.
Для задачи о частных суммах, хотя операция sum вполне изучена, testsum все еще не имеет строгих границ для определенных диапазонов параметров [6]. Кроме того, получение строгих границ в модели битового зонда для частных сумм в [math]\displaystyle{ \mathbb{Z}_2 }[/math] представляется довольно сложной задачей.
Литература
1. Alstrup, S., Husfeldt, T., Rauhe,T.: Marked ancestor problems. In: Proc. 39th IEEE Symposium on Foundations of Computer Science (FOCS), 1998, pp. 534-543
2. Eppstein, D., Italiano, G.F., Tamassia, R., Tarjan, R.E., Westbrook, J.R., Yung, M.: Maintenance of a minimum spanning forest in a dynamic planar graph. J. Algorithms 13,33-54 (1992). See also SODA'90
3. Fredman, M.L., Saks, M.E.: The cell probe complexity of dynamic data structures. In: Proc. 21st ACM Symposium on Theory of Computing (STOC), 1989, pp. 345-354
4. Husfeldt, T., Rauhe, T.: New lower bound techniques for dynamic partial sums and related problems. SIAM J. Comput. 32,736-753 (2003). See also ICALP'98
5. Miltersen, P.B.: Cell probe complexity-a survey. In: 19th Conference on the Foundations of Software Technology and Theoretical Computer Science (FSTTCS), 1999 (Advances in Data Structures Workshop)
6. Patrascu, M. and Demaine, E.D.: Logarithmic lower bounds in the cell-probe model. SIAM J. Comput. 35, 932-963 (2006). See also SODA'04 and STOC'04
7. Patrascu, M., Tarnija, C.: On dynamic bit-probe complexity. Theor. Comput. Sci. 380,127-142 (2007). See also ICALP'05
8. Sleator, D.D., Tarjan, R.E.: A data structure for dynamic trees. J. Comput. Syst. Sci. 26, 362-391 (1983). See also STOC'81
9. Thorup, M.: Near-optimal fully-dynamic graph connectivity. In: Proc. 32nd ACM Symposium on Theory of Computing (STOC), 2000, pp. 343-350