Переименование: различия между версиями
Irina (обсуждение | вклад) |
Irina (обсуждение | вклад) |
||
| (не показано 11 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
== Ключевые слова и синонимы == | == Ключевые слова и синонимы == | ||
Переименование без ожидания | Переименование без ожидания (''Wait-free renaming'') | ||
== Постановка задачи == | == Постановка задачи == | ||
| Строка 18: | Строка 18: | ||
== Основные результаты == | == Основные результаты == | ||
'''Теорема 1. Пусть <math>S^n</math> – n-симплекс, а <math>S^m</math> – грань <math>S^n</math>. Обозначим за S комплекс, состоящий из всех граней <math>S^m</math>, за <math>\dot{S}</math> – комплекс, состоящий из всех собственных граней <math>S^n</math> (граничный комплекс <math>S</math>). Если <math>\sigma( \dot{S})</math> – подразделение S, а <math>\phi: \sigma (\dot{S}) \to \mathcal{F}(S)</math> – симплициальная карта, то существуют подразделение <math>\tau(S)</math> и симплициальная карта <math>\psi: \tau (\dot{S}) \to \mathcal{F}(S)</math>, такие, что <math>\tau (\dot{S}) = \sigma (\dot{S})</math>, и <math>\phi</math> и <math>\psi</math> сходятся (согласуются) на <math>\sigma (\dot{S})</math>.''' | '''Теорема 1. Пусть <math>S^n</math> – n-симплекс, а <math>S^m</math> – грань <math>S^n</math>. Обозначим за <math>S</math> комплекс, состоящий из всех граней <math>S^m</math>, за <math>\dot{S}</math> – комплекс, состоящий из всех собственных граней <math>S^n</math> (граничный комплекс <math>S</math>). Если <math>\sigma( \dot{S})</math> – подразделение <math>S</math>, а <math>\phi: \sigma (\dot{S}) \to \mathcal{F}(S)</math> – симплициальная карта, то существуют подразделение <math>\tau(S)</math> и симплициальная карта <math>\psi: \tau (\dot{S}) \to \mathcal{F}(S)</math>, такие, что <math>\tau (\dot{S}) = \sigma (\dot{S})</math>, и <math>\phi</math> и <math>\psi</math> сходятся (согласуются) на <math>\sigma (\dot{S})</math>.''' | ||
Неформально, любая симплициальная карта m-сферы в F может быть «заполнена» до симплициальной карты (m + 1)-диска. Остовом для F( | Неформально, любая симплициальная карта m-сферы в <math>\mathcal{F}</math> может быть «заполнена» до симплициальной карты (m + 1)-диска. ''Остовом'' для <math>\mathcal{F}(S^n)</math> является подразделение <math>\sigma</math> входного симплекса <math>S^n</math> вместе с симплициальной картой <math>\phi: \sigma(S^n) \to \mathcal{F}(S^n)</math>, такое, что для каждой грани <math>S^m</math> из <math>S^n</math> выполняется соотношение <math>\phi: \sigma(S^m) \to \mathcal{F}(S^m)</math>. Остовы строятся по одной размерности за раз. Для каждого <math> \vec s = \langle P_i, v_i \rangle \in S^n \; \phi</math> переносит <math> \vec s</math> для одиночного выполнения <math>P_i</math> с входным значением <math> \vec v_i</math>. Для каждого <math>S^1 = (\vec s_0, \vec s_1)</math> из теоремы 1 следует, что <math>\phi(\vec s_0)</math> и <math>\phi(\vec s_1)</math> могут быть соединены путем в <math>\mathcal{F}(S^1)</math>. Для каждого <math>S^1 = (\vec s_0, \vec s_1, \vec s_2)</math> построенные по индукции остовы определяют каждую грань граничного комплекса <math>\phi: \sigma(S^1_{ij}) \to \mathcal{F}(S^1)_{ij}</math> для <math>i, j \in \{ 0, 1, 2 \}</math>. Из теоремы 1 следует, что эту карту можно «заполнить», распространив подразделение с граничного комплекса на весь комплекс. | ||
Теорема 2. Если у задачи принятия решения имеется протокол в асинхронной памяти чтения/записи, то каждый входной симплекс имеет остов. | '''Теорема 2. Если у задачи принятия решения имеется протокол в асинхронной памяти чтения/записи, то каждый входной симплекс имеет остов.''' | ||
| Строка 30: | Строка 30: | ||
Определение 1. Протокол основан на сравнении, если единственные операции, которые процесс может выполнять над идентификаторами процессора – это проверка на равенство и порядок; то есть, если даны два P и Q, процесс может проверить P = Q, P < | '''Определение 1'''. Протокол ''основан на сравнении'', если единственные операции, которые процесс может выполнять над идентификаторами процессора – это проверка на равенство и порядок; то есть, если даны два P и Q, процесс может проверить выполнимость <math>P = Q, P \le Q</math> и <math>P \ge Q</math>, но не может исследовать структуру идентификаторов более подробно. | ||
Лемма 3. Если существует протокол переименования для K имен, не требующий ожидания, то существует и протокол, основанный на сравнении. | '''Лемма 3'''. Если существует протокол переименования для K имен, не требующий ожидания, то существует и протокол, основанный на сравнении. | ||
Доказательство. Аттия и др. [ ] предложили простой протокол переименования без ожидания, основанный на сравнении, который использует 2n+1 выходных имен. Применим этот алгоритм для присвоения каждому процессу промежуточного имени, а затем используем это промежуточное имя в качестве входных данных для протокола с K именами. □ | Доказательство. Аттия и др. [1] предложили простой протокол переименования без ожидания, основанный на сравнении, который использует 2n+1 выходных имен. Применим этот алгоритм для присвоения каждому процессу ''промежуточного'' имени, а затем используем это промежуточное имя в качестве входных данных для протокола с K именами. □ | ||
Алгоритмы, основанные на сравнении, симметричны относительно границы остова. Пусть | Алгоритмы, основанные на сравнении, ''симметричны'' относительно границы остова. Пусть <math>S^n</math> – входной симплекс, <math>\phi: \sigma(S^n) \to \mathcal{F}(S^n)</math> – остов, а <math>\mathcal{R}</math> – выходной комплекс для 2n имен. Компоновка карты остова <math>\phi</math> и карты решений <math>\delta</math> дает карту <math>\sigma(S^n) \to \mathcal{R}</math>. Эту карту можно упростить, заменив каждое выходное имя его четностью и заменив комплекс <math>\mathcal{R}</math> бинарной n-сферой <math>\mathcal{B}^n</math>. | ||
(1) | (1) <math>\mu : \sigma(S^n) \to \mathcal{B}^n</math>. | ||
Обозначим симплекс | Обозначим симплекс <math>\mathcal{B}^n</math>, все значения которого равны нулю, как <math>0^n</math>, а симплекс со всеми единицами – как <math>1^n</math>. | ||
Лемма 4. | '''Лемма 4'''. <math> \mu^{-1} (0^N) = \mu^{-1} (1^n) = 0</math>. | ||
Доказательство. В диапазоне 0...: ; 2 n - 1 не содержится n + 1 различных четных или n + 1 различных нечетных имен. □ | Доказательство. В диапазоне 0...: ; 2 n - 1 не содержится n + 1 различных четных или n + 1 различных нечетных имен. □ | ||
Назовем n-цилиндром бинарную n-сферу без | Назовем ''n-цилиндром'' <math>C^n</math> бинарную n-сферу без <math>0^n</math> и <math>1^n</math>. Неформально, остальная часть аргументации сводится к тому, чтобы показать, что граница остова «оборачивается» вокруг отверстия в <math>C^n</math> ненулевое число раз. | ||
Остов | Остов <math>\sigma(S^n)</math> (в действительности, любой любой подразделенный n-симплекс) представляет собой (комбинаторное) ''многообразие с границей'': каждый (n – 1)-симплекс является гранью либо одного, либо двух n-симплексов. Если он является гранью двух n-симплексов, то симплекс является ''внутренним'', в противном случае – ''граничным''. Ориентация <math>S^n</math> порождает ориентацию каждого n-симплекса из <math>\sigma(S^n)</math>, так что каждый внутренний (n – 1)-симплекс наследует противоположные ориентации. Суммирование этих ориентированных симплексов дает цепь, обозначаемую <math>\sigma_*(S^n)</math>, такую, что <math>\partial \sigma_* (S^n) = \sum^n_{i = 0} (-1)^i \sigma_* (face_i(S^n))</math>. | ||
| Строка 61: | Строка 61: | ||
Теорема 5. Пусть цепь | '''Теорема 5. Пусть цепь <math>0^n</math> – это симплекс <math>0^n</math>, ориентированный как <math>S^n</math>. (1) При 0 < m < n любые два m-цикла гомологичны, и (2) каждый n-цикл <math>C^n</math> гомологичен <math>k \cdot \partial O^n</math> для некоторого целого числа k. <math>C^n</math> является границей тогда и только тогда, когда k = 0.''' | ||
Пусть <math>S^m</math> – грань <math>S^n</math>, натянутая на одиночные выполнения <math>P_0, ..., P_m</math>. Обозначим за <math>0^m</math> некоторый m-симплекс из <math>C^n</math>, все значения которого равны нулю. Какой именно, будет понятно из контекста. | |||
'''Лемма 6.''' Для каждой собственной грани <math>S^{m - 1}</math> симплекса <math>S^n</math> существует m-цепь <math>\alpha(S^{m-1})</math>, такая, что <math>\mu_* (\sigma_* (S^m)) - 0^m - \sum^m_{i = 0} (-1)^i \alpha (face_i(S^m))</math> является циклом. | |||
Доказательство путем индукции по m. При m = 1 <math>ids(S^1) = \{ i, j \}</math>. <math>0^1</math> и <math>\mu_* (\sigma_* (S^1))</math> – 1-цепи с общей границей <math>\langle P_i, 0 \rangle – \langle P_j, 0 \rangle</math>, поэтому <math>\mu_* (\sigma_* (S^1)) - 0^1</math> является циклом, и <math>\alpha \langle \langle P_i, 0 \rangle \rangle </math>. | |||
является | Предположим, что утверждение верно для <math>m, 1 \ge m < n – 1</math>. Согласно теореме 5, каждый m-цикл является граничным (для m < n – 1), поэтому существует (m + 1)-цепь <math>\alpha(S^m)</math>, такая, что <math>\mu_* (\sigma_* (S^m)) - 0^m - \sum^m_{i = 0} (-1)^i \alpha (face_i(S^m)) = \partial \alpha(S^m)</math>. | ||
Если взять знакопеременную сумму по граням <math>S^{m+1}</math>, то <math>\alpha (face_i(S^m))</math> сокращается, что дает <math>\mu_* (\partial \sigma_* (S^{m + 1})) - \partial 0^{m + 1} = \sum^{m + 1}_{i = 0} (-1)^i \partial \alpha (face_i(S^{m + 1}))</math>. | |||
Перестановка членов дает <math>\partial \Bigg ( \mu_* (\sigma_* (S^{m + 1})) - 0^{m + 1} - \sum^{m + 1}_{i = 0} (-1)^i \alpha (face_i(S^{m + 1})) \Bigg ) = 0</math>, из чего следует, что <math>\mu_* (\sigma_* (S^{m + 1})) - 0^{m + 1} - \sum^{m + 1}_{i = 0} (-1)^i \alpha (face_i(S^{m + 1}))</math> является (m + 1)-циклом. □ | |||
'''Теорема 7. Не существует протокола переименования без ожидания для (n + 1) процессов, использующих 2n выходных имен.''' | |||
Доказательство. Поскольку <math>\mu_* (\sigma_* (S^{n - 1})) - 0^{n - 1} - \sum^{n}_{i = 0} (-1)^i \alpha (face_i(S^{n - 1}))</math> является циклом, из теоремы 5 следует, что она гомологична <math>k \cdot \partial 0^n</math> для некоторого целого числа k. Поскольку <math>\mu</math> симметрична на границе <math>\sigma(S^n)</math>, знакопеременная сумма по (n – 1)-мерным граням <math>S^n</math> дает: | |||
<math>\mu_* (\partial \sigma_* (S^n)) - \partial 0^n \sim (n + 1) k \cdot \partial 0^n</math> | |||
или | |||
<math>\mu_* (\partial \sigma_* (S^n)) \sim (1 + (n + 1) k) \cdot \partial 0^n</math>. | |||
Поскольку не существует значения k, для которого (1 + (n+1)k) равно нулю, цикл | Поскольку не существует значения k, для которого (1 + (n + 1)k) равно нулю, цикл <math>\mu_* (\partial \sigma_* (S^n))</math> не является границей, что противоречит предположению. □ | ||
□ | |||
== Применение == | == Применение == | ||
| Строка 115: | Строка 108: | ||
2. Herlihy, M.P., Shavit, N.: The asynchronous computability theorem for t-resilient tasks. In: Proceedings 25th Annual ACM Symposium on Theory of Computing, 1993, pp. 111-120 | 2. Herlihy, M.P., Shavit, N.: The asynchronous computability theorem for t-resilient tasks. In: Proceedings 25th Annual ACM Symposium on Theory of Computing, 1993, pp. 111-120 | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 11:43, 18 февраля 2025
Ключевые слова и синонимы
Переименование без ожидания (Wait-free renaming)
Постановка задачи
Рассмотрим систему, в которой n + 1 процессов [math]\displaystyle{ P_0, ..., P_n }[/math] взаимодействуют либо путем передачи сообщений, либо путем чтения из общей памяти и записи в нее. Процессы являются асинхронными: не существует верхних или нижних ограничений на их скорость, и до t из них могут уйти в необнаружимый отказ путем останова. В задаче переименования, которую предложили Аттия, Бар-Ной, Долев, Пелег и Райшук [1], каждый процесс получает уникальное входное имя из диапазона 0, ..., N и выбирает уникальное выходное имя из строго меньшего диапазона 0, ..., K. Чтобы исключить тривиальные решения, функция принятия решения процесса должна зависеть только от входных имен, а не от его заранее назначенного идентификатора (так что Pi не может просто выбрать выходное имя i). Аттия и коллеги показали, что задача не имеет решения при К = n, но имеет решение при К = N + t. В 1993 году Херлихи и Шавит [2] продемонстрировали, что задача не имеет решения при К < N + t.
Вершины, симплексы и комплексы моделируют задачи принятия решений. (См. сопутствующую статью Топологический подход в распределенных вычислениях). Состояние процесса в начале или конце задачи представляется в виде вершины [math]\displaystyle{ \vec v }[/math], помеченной идентификатором процесса и значением (входным или выходным): [math]\displaystyle{ \vec v = \langle P, v_i \rangle }[/math]. Две такие вершины совместимы, если: (1) у них разные идентификаторы процессов и (2) этим процессам можно присвоить эти значения вместе. Например, в задаче переименования входные значения должны быть разными, поэтому две входные вершины совместимы только в том случае, если они помечены разными идентификаторами процессов и разными входными значениями.
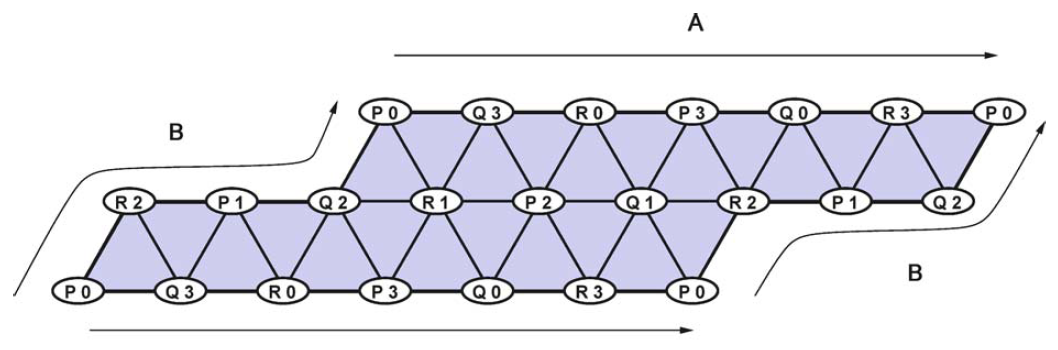
На рисунке 1 показан выходной комплекс для задачи переименования трех процессов с использованием четырех имен. Обратите внимание, что два ребра, помеченные A, идентичны, так же как и два ребра, помеченные B. Идентифицируя эти ребра, задача определяет симплициальный комплекс, топологически эквивалентный тору. Разумеется, после изменения количества процессов или количества имен этот комплекс перестает быть тором.
Рис. 1. Выходной комплекс для задачи переименования трех процессов с использованием четырех имен
Основные результаты
Теорема 1. Пусть [math]\displaystyle{ S^n }[/math] – n-симплекс, а [math]\displaystyle{ S^m }[/math] – грань [math]\displaystyle{ S^n }[/math]. Обозначим за [math]\displaystyle{ S }[/math] комплекс, состоящий из всех граней [math]\displaystyle{ S^m }[/math], за [math]\displaystyle{ \dot{S} }[/math] – комплекс, состоящий из всех собственных граней [math]\displaystyle{ S^n }[/math] (граничный комплекс [math]\displaystyle{ S }[/math]). Если [math]\displaystyle{ \sigma( \dot{S}) }[/math] – подразделение [math]\displaystyle{ S }[/math], а [math]\displaystyle{ \phi: \sigma (\dot{S}) \to \mathcal{F}(S) }[/math] – симплициальная карта, то существуют подразделение [math]\displaystyle{ \tau(S) }[/math] и симплициальная карта [math]\displaystyle{ \psi: \tau (\dot{S}) \to \mathcal{F}(S) }[/math], такие, что [math]\displaystyle{ \tau (\dot{S}) = \sigma (\dot{S}) }[/math], и [math]\displaystyle{ \phi }[/math] и [math]\displaystyle{ \psi }[/math] сходятся (согласуются) на [math]\displaystyle{ \sigma (\dot{S}) }[/math].
Неформально, любая симплициальная карта m-сферы в [math]\displaystyle{ \mathcal{F} }[/math] может быть «заполнена» до симплициальной карты (m + 1)-диска. Остовом для [math]\displaystyle{ \mathcal{F}(S^n) }[/math] является подразделение [math]\displaystyle{ \sigma }[/math] входного симплекса [math]\displaystyle{ S^n }[/math] вместе с симплициальной картой [math]\displaystyle{ \phi: \sigma(S^n) \to \mathcal{F}(S^n) }[/math], такое, что для каждой грани [math]\displaystyle{ S^m }[/math] из [math]\displaystyle{ S^n }[/math] выполняется соотношение [math]\displaystyle{ \phi: \sigma(S^m) \to \mathcal{F}(S^m) }[/math]. Остовы строятся по одной размерности за раз. Для каждого [math]\displaystyle{ \vec s = \langle P_i, v_i \rangle \in S^n \; \phi }[/math] переносит [math]\displaystyle{ \vec s }[/math] для одиночного выполнения [math]\displaystyle{ P_i }[/math] с входным значением [math]\displaystyle{ \vec v_i }[/math]. Для каждого [math]\displaystyle{ S^1 = (\vec s_0, \vec s_1) }[/math] из теоремы 1 следует, что [math]\displaystyle{ \phi(\vec s_0) }[/math] и [math]\displaystyle{ \phi(\vec s_1) }[/math] могут быть соединены путем в [math]\displaystyle{ \mathcal{F}(S^1) }[/math]. Для каждого [math]\displaystyle{ S^1 = (\vec s_0, \vec s_1, \vec s_2) }[/math] построенные по индукции остовы определяют каждую грань граничного комплекса [math]\displaystyle{ \phi: \sigma(S^1_{ij}) \to \mathcal{F}(S^1)_{ij} }[/math] для [math]\displaystyle{ i, j \in \{ 0, 1, 2 \} }[/math]. Из теоремы 1 следует, что эту карту можно «заполнить», распространив подразделение с граничного комплекса на весь комплекс.
Теорема 2. Если у задачи принятия решения имеется протокол в асинхронной памяти чтения/записи, то каждый входной симплекс имеет остов.
Можно ограничиться протоколами, которые обладают тем свойством, что любой процесс выбирает одно и то же имя при одиночном выполнении.
Определение 1. Протокол основан на сравнении, если единственные операции, которые процесс может выполнять над идентификаторами процессора – это проверка на равенство и порядок; то есть, если даны два P и Q, процесс может проверить выполнимость [math]\displaystyle{ P = Q, P \le Q }[/math] и [math]\displaystyle{ P \ge Q }[/math], но не может исследовать структуру идентификаторов более подробно.
Лемма 3. Если существует протокол переименования для K имен, не требующий ожидания, то существует и протокол, основанный на сравнении.
Доказательство. Аттия и др. [1] предложили простой протокол переименования без ожидания, основанный на сравнении, который использует 2n+1 выходных имен. Применим этот алгоритм для присвоения каждому процессу промежуточного имени, а затем используем это промежуточное имя в качестве входных данных для протокола с K именами. □
Алгоритмы, основанные на сравнении, симметричны относительно границы остова. Пусть [math]\displaystyle{ S^n }[/math] – входной симплекс, [math]\displaystyle{ \phi: \sigma(S^n) \to \mathcal{F}(S^n) }[/math] – остов, а [math]\displaystyle{ \mathcal{R} }[/math] – выходной комплекс для 2n имен. Компоновка карты остова [math]\displaystyle{ \phi }[/math] и карты решений [math]\displaystyle{ \delta }[/math] дает карту [math]\displaystyle{ \sigma(S^n) \to \mathcal{R} }[/math]. Эту карту можно упростить, заменив каждое выходное имя его четностью и заменив комплекс [math]\displaystyle{ \mathcal{R} }[/math] бинарной n-сферой [math]\displaystyle{ \mathcal{B}^n }[/math].
(1) [math]\displaystyle{ \mu : \sigma(S^n) \to \mathcal{B}^n }[/math].
Обозначим симплекс [math]\displaystyle{ \mathcal{B}^n }[/math], все значения которого равны нулю, как [math]\displaystyle{ 0^n }[/math], а симплекс со всеми единицами – как [math]\displaystyle{ 1^n }[/math].
Лемма 4. [math]\displaystyle{ \mu^{-1} (0^N) = \mu^{-1} (1^n) = 0 }[/math].
Доказательство. В диапазоне 0...: ; 2 n - 1 не содержится n + 1 различных четных или n + 1 различных нечетных имен. □
Назовем n-цилиндром [math]\displaystyle{ C^n }[/math] бинарную n-сферу без [math]\displaystyle{ 0^n }[/math] и [math]\displaystyle{ 1^n }[/math]. Неформально, остальная часть аргументации сводится к тому, чтобы показать, что граница остова «оборачивается» вокруг отверстия в [math]\displaystyle{ C^n }[/math] ненулевое число раз.
Остов [math]\displaystyle{ \sigma(S^n) }[/math] (в действительности, любой любой подразделенный n-симплекс) представляет собой (комбинаторное) многообразие с границей: каждый (n – 1)-симплекс является гранью либо одного, либо двух n-симплексов. Если он является гранью двух n-симплексов, то симплекс является внутренним, в противном случае – граничным. Ориентация [math]\displaystyle{ S^n }[/math] порождает ориентацию каждого n-симплекса из [math]\displaystyle{ \sigma(S^n) }[/math], так что каждый внутренний (n – 1)-симплекс наследует противоположные ориентации. Суммирование этих ориентированных симплексов дает цепь, обозначаемую [math]\displaystyle{ \sigma_*(S^n) }[/math], такую, что [math]\displaystyle{ \partial \sigma_* (S^n) = \sum^n_{i = 0} (-1)^i \sigma_* (face_i(S^n)) }[/math].
Ниже приводится стандартный вывод о гомологии сфер.
Теорема 5. Пусть цепь [math]\displaystyle{ 0^n }[/math] – это симплекс [math]\displaystyle{ 0^n }[/math], ориентированный как [math]\displaystyle{ S^n }[/math]. (1) При 0 < m < n любые два m-цикла гомологичны, и (2) каждый n-цикл [math]\displaystyle{ C^n }[/math] гомологичен [math]\displaystyle{ k \cdot \partial O^n }[/math] для некоторого целого числа k. [math]\displaystyle{ C^n }[/math] является границей тогда и только тогда, когда k = 0.
Пусть [math]\displaystyle{ S^m }[/math] – грань [math]\displaystyle{ S^n }[/math], натянутая на одиночные выполнения [math]\displaystyle{ P_0, ..., P_m }[/math]. Обозначим за [math]\displaystyle{ 0^m }[/math] некоторый m-симплекс из [math]\displaystyle{ C^n }[/math], все значения которого равны нулю. Какой именно, будет понятно из контекста.
Лемма 6. Для каждой собственной грани [math]\displaystyle{ S^{m - 1} }[/math] симплекса [math]\displaystyle{ S^n }[/math] существует m-цепь [math]\displaystyle{ \alpha(S^{m-1}) }[/math], такая, что [math]\displaystyle{ \mu_* (\sigma_* (S^m)) - 0^m - \sum^m_{i = 0} (-1)^i \alpha (face_i(S^m)) }[/math] является циклом.
Доказательство путем индукции по m. При m = 1 [math]\displaystyle{ ids(S^1) = \{ i, j \} }[/math]. [math]\displaystyle{ 0^1 }[/math] и [math]\displaystyle{ \mu_* (\sigma_* (S^1)) }[/math] – 1-цепи с общей границей [math]\displaystyle{ \langle P_i, 0 \rangle – \langle P_j, 0 \rangle }[/math], поэтому [math]\displaystyle{ \mu_* (\sigma_* (S^1)) - 0^1 }[/math] является циклом, и [math]\displaystyle{ \alpha \langle \langle P_i, 0 \rangle \rangle }[/math].
Предположим, что утверждение верно для [math]\displaystyle{ m, 1 \ge m \lt n – 1 }[/math]. Согласно теореме 5, каждый m-цикл является граничным (для m < n – 1), поэтому существует (m + 1)-цепь [math]\displaystyle{ \alpha(S^m) }[/math], такая, что [math]\displaystyle{ \mu_* (\sigma_* (S^m)) - 0^m - \sum^m_{i = 0} (-1)^i \alpha (face_i(S^m)) = \partial \alpha(S^m) }[/math].
Если взять знакопеременную сумму по граням [math]\displaystyle{ S^{m+1} }[/math], то [math]\displaystyle{ \alpha (face_i(S^m)) }[/math] сокращается, что дает [math]\displaystyle{ \mu_* (\partial \sigma_* (S^{m + 1})) - \partial 0^{m + 1} = \sum^{m + 1}_{i = 0} (-1)^i \partial \alpha (face_i(S^{m + 1})) }[/math].
Перестановка членов дает [math]\displaystyle{ \partial \Bigg ( \mu_* (\sigma_* (S^{m + 1})) - 0^{m + 1} - \sum^{m + 1}_{i = 0} (-1)^i \alpha (face_i(S^{m + 1})) \Bigg ) = 0 }[/math], из чего следует, что [math]\displaystyle{ \mu_* (\sigma_* (S^{m + 1})) - 0^{m + 1} - \sum^{m + 1}_{i = 0} (-1)^i \alpha (face_i(S^{m + 1})) }[/math] является (m + 1)-циклом. □
Теорема 7. Не существует протокола переименования без ожидания для (n + 1) процессов, использующих 2n выходных имен.
Доказательство. Поскольку [math]\displaystyle{ \mu_* (\sigma_* (S^{n - 1})) - 0^{n - 1} - \sum^{n}_{i = 0} (-1)^i \alpha (face_i(S^{n - 1})) }[/math] является циклом, из теоремы 5 следует, что она гомологична [math]\displaystyle{ k \cdot \partial 0^n }[/math] для некоторого целого числа k. Поскольку [math]\displaystyle{ \mu }[/math] симметрична на границе [math]\displaystyle{ \sigma(S^n) }[/math], знакопеременная сумма по (n – 1)-мерным граням [math]\displaystyle{ S^n }[/math] дает:
[math]\displaystyle{ \mu_* (\partial \sigma_* (S^n)) - \partial 0^n \sim (n + 1) k \cdot \partial 0^n }[/math]
или
[math]\displaystyle{ \mu_* (\partial \sigma_* (S^n)) \sim (1 + (n + 1) k) \cdot \partial 0^n }[/math].
Поскольку не существует значения k, для которого (1 + (n + 1)k) равно нулю, цикл [math]\displaystyle{ \mu_* (\partial \sigma_* (S^n)) }[/math] не является границей, что противоречит предположению. □
Применение
Задача переименования является ключевым инструментом для понимания возможностей различных асинхронных моделей вычислений.
Открытые вопросы
Определение всех возможностей топологического подхода для доказательства нижних границ остается нерешенной задачей.
См. также
- Невозможность асинхронного консенсуса
- Согласование множеств
- Топологический подход в распределенных вычислениях
Литература
1. Attiya, H., Bar-Noy, A., Dolev, D., Peleg, D., Reischuk, R.: Renaming in an asynchronous environment. J. ACM 37(3), 524-548 (1990)
2. Herlihy, M.P., Shavit, N.: The asynchronous computability theorem for t-resilient tasks. In: Proceedings 25th Annual ACM Symposium on Theory of Computing, 1993, pp. 111-120