Технологическое отображение последовательной схемы: различия между версиями
Irina (обсуждение | вклад) |
KVN (обсуждение | вклад) |
||
| (не показано 15 промежуточных версий 1 участника) | |||
| Строка 3: | Строка 3: | ||
== Постановка задачи == | == Постановка задачи == | ||
Одним из ключевых этапов процесса проектирования СБИС является технологическое отображение, которое преобразует булеву сеть технологически инвариантных логических вентилей и D-триггеров, тактируемых перепадом напряжения (FF) в эквивалентную сеть, состоящую из ячеек из библиотеки логических элементов целевой технологии [1, , 5]. Технологическое отображение может быть сформулировано как задача покрытия, в которой осуществляется покрытие логических вентилей элементами технологической библиотеки. Для простоты изложения предположим, что библиотека содержит только один элемент – таблицу поиска с K логическими входами (K-LUT) с единичной задержкой. Таблица K-LUT может реализовать любую булеву функцию с не более чем K входами, как в случае с высокоэффективными программируемыми пользователем вентильными матрицами (ППВМ | Одним из ключевых этапов процесса проектирования СБИС является технологическое отображение, которое преобразует булеву сеть, состоящую из технологически инвариантных логических вентилей и D-триггеров, тактируемых перепадом напряжения (FF), в эквивалентную сеть, состоящую из ячеек из библиотеки логических элементов целевой технологии [1, 3, 5]. Технологическое отображение может быть сформулировано как задача покрытия, в которой осуществляется покрытие логических вентилей элементами технологической библиотеки. Для простоты изложения предположим, что библиотека содержит только один элемент – таблицу поиска с K логическими входами (K-LUT) с единичной задержкой. Таблица K-LUT может реализовать любую булеву функцию с не более чем K входами, как в случае с высокоэффективными программируемыми пользователем вентильными матрицами (ППВМ). | ||
Пример технологического отображения приведен на рис. 1. Для исходной сети на схеме (1) с тремя триггерами и четырьмя вентилями строится покрытие | Пример технологического отображения приведен на рис. 1. Для исходной сети на схеме (1) с тремя триггерами и четырьмя вентилями строится покрытие тремя 3-входовыми конусами, как показано на рис. 1 (2). Соответствующее отображение с использованием таблиц 3-LUT показано на рис. 1 (3). Заметим, что вентиль i покрывается двумя конусами. У отображения на рис. 1 (3) ''продолжительность цикла'' (или ''период цикла'') составляет две единицы, что равняется совокупной задержке на самом длинном пути между триггерами (FF), от первичных входов (PI) до триггеров и от триггеров до первичных выходов (PO). | ||
| Строка 19: | Строка 19: | ||
[[Файл:SCTM_2.png]] | [[Файл:SCTM_2.png]] | ||
Рисунок 2. Ресинхронизация и отображение: (1) ресинхронизация и | Рисунок 2. Ресинхронизация и отображение: (1) ресинхронизация и покрытие, (2) отображение, (3) решение после ресинхронизации | ||
K-ограниченной сетью называется сеть, в которой каждый вентиль имеет не более K входов. Задачу технологического отображения последовательной схемы можно определить следующим образом. Пусть даны K-ограниченная булева сеть N и целевая продолжительность цикла | ''K-ограниченной сетью'' называется сеть, в которой каждый вентиль имеет не более K входов. Задачу технологического отображения последовательной схемы можно определить следующим образом. Пусть даны K-ограниченная булева сеть N и целевая продолжительность цикла <math>\varphi</math>. Найти отображение с продолжительностью цикла <math>\varphi</math>, предполагая, что допускается перемещение триггеров при помощи ресинхронизации. | ||
== Основные результаты == | == Основные результаты == | ||
| Строка 28: | Строка 28: | ||
В [7] был представлен другой алгоритм, который использовал преимущество знания того факта, что на практике K является небольшим целым числом, обычно от 3 до 6. Алгоритм выполняет перечисление всех K-входовых конусов для каждого вентиля. Он может учитывать другие целевые показатели оптимизации (например, площадь и мощность) и может применяться к стандартным библиотекам логических элементов. | В работе [7] был представлен другой алгоритм, который использовал преимущество знания того факта, что на практике K является небольшим целым числом, обычно от 3 до 6. Алгоритм выполняет перечисление всех K-входовых конусов для каждого вентиля. Он может учитывать другие целевые показатели оптимизации (например, площадь и мощность) и может применяться к стандартным библиотекам логических элементов. | ||
'''Перечисление разрезов''' | '''Перечисление разрезов''' | ||
Булева сеть может быть представлена в виде ориентированного графа со взвешенными ребрами, вершинами которого являются логические вентили, первичные входы и первичные выходы. | Булева сеть может быть представлена в виде ориентированного графа со взвешенными ребрами, вершинами которого являются логические вентили, первичные входы и первичные выходы. В нем имеется ориентированное ребро (u, v) с весом d, если u, после прохода через d триггеров, воздействует на v. | ||
Логический конус для вершины может быть представлен в виде разреза, состоящего из входов конуса. Элемент разреза для v состоит из задающей вершины u и суммарного веса d на путях из u в v, обозначаемого | Логический конус для вершины может быть представлен в виде ''разреза'', состоящего из входов конуса. Элемент разреза для v состоит из задающей вершины u и суммарного веса d на путях из u в v, обозначаемого <math>u^d</math>. Если u достигает v по нескольким путям с разным числом триггеров, u будет входить в разрез несколько раз с разными значениями d. К примеру, для конуса для z на рис 2 (2) соответствующий разрез будет иметь вид <math>\{ z^1, a^1, b^1 \}</math>. Разрез размера K называется K-разрезом. | ||
Пусть ( | Пусть <math>(u_i, v)</math> – ребро в N с весом <math>d_i</math>, а <math>C(u_i)</math> – множество K-разрезов для <math>d_i</math>, i = 1, ..., t. Обозначим за <math>merge(C(u_1), ..., C(u_t))</math> следующую операцию на множествах: | ||
<math>\{ \{ v^0 \} \} \cup \{ c^{d_1}_1 \cup ... \cup c^{d_t}_t | c_1 \in C(u_1), ..., c_t \in C(u_t), | c^{d_1}_1 \cup ... \cup c^{d_t}_t | \le K \}</math>, | |||
Если в сети N не имеется циклов, | где <math>c^{d_i}_i = \{ u^{d + d_i} | u^d \in c_i \}</math> для i = 1, ..., t. Очевидно, что <math>merge(C(u_1), ..., C(u_t))</math> является множеством K-разрезов для v. | ||
Если в сети N не имеется циклов, K-разрезы для всех вершин можно определить при помощи операции слияния merge в топологическом порядке, начиная с первичных входов. Для сетей общего вида на рис. 3 представлена процедура итеративного вычисления разрезов, предложенная в работе [7]. | |||
На рис. 4 изображены итерации перечисления 3-разрезов для схемы на рис. 1 (1) при слиянии разрезов в порядке i, x, y, z, o. В начале работы каждая вершина имеет собственный тривиальный разрез, включающий ее саму. В ряду 1 представлены новые разрезы, обнаруженные на первой итерации. На второй итерации обнаруживаются еще два новых разреза (для x). После этого выполнение процедуры останавливается, так как последующие слияния не приводят к выявлению новых разрезов. | На рис. 4 изображены итерации перечисления 3-разрезов для схемы на рис. 1 (1) при слиянии разрезов в порядке i, x, y, z, o. В начале работы каждая вершина имеет собственный тривиальный разрез, включающий ее саму. В ряду 1 представлены новые разрезы, обнаруженные на первой итерации. На второй итерации обнаруживаются еще два новых разреза (для x). После этого выполнение процедуры останавливается, так как последующие слияния не приводят к выявлению новых разрезов. | ||
FindAllCuts(N, K) | '''FindAllCuts'''(N, K) | ||
foreach | '''foreach''' вершины v в N '''do''' <math>C(v) \Leftarrow \{ \{ v^0 \} \}</math> | ||
while (находятся новые разрезы) do | '''while''' (находятся новые разрезы) '''do''' | ||
foreach | '''foreach''' вершины v в N '''do''' <math>C(v) \Leftarrow merge(C(u_1), ..., C(u_t))</math> | ||
Рисунок 3. Процедура перечисления разрезов | Рисунок 3. Процедура перечисления разрезов | ||
0 { | {| class="wikitable" style="text-align:center" | ||
1 | |- | ||
2 | ! Итер. !! a !! b !! i !! x !! y !! z !! o | ||
|- | |||
! 0 | |||
| <math>\{ a^0 \}</math> || <math>\{ b^0 \}</math> || <math>\{ i^0 \}</math> || <math>\{ x^0 \}</math> || <math>\{ y^0 \}</math> || <math>\{ z^0 \}</math> || <math>\{ o^0 \}</math> | |||
|- | |||
! 1 | |||
| || || <math>\{ a^0 \}</math> | |||
|| <math>\{ i^1, z^1 \}</math> | |||
<math>\{ a^1, z^1 \}</math> | |||
|| <math>\{ i^0, b^0, z^0 \}</math> | |||
<math>\{ a^0, b^0, z^0 \}</math> | |||
|| | |||
<math>\{ x^0, y^1 \}</math> | |||
<math>\{ i^1, z^1, b^1 \}</math> | |||
<math>\{ a^1, z^1, b^1 \}</math> | |||
<math>\{ i^1, z^1, y^1 \}</math> | |||
<math>\{ a^1, z^1, y^1 \}</math> | |||
|| | |||
<math>\{ z^0 \}</math> | |||
|- | |||
! 2 | |||
| || || || <math>\{ i^1, x^1, y^2 \}</math> | |||
<math> \{ a^1, x^1, y^2 \} </math> | |||
|| || || | |||
|} | |||
Рисунок 4. Пример перечисления разрезов | Рисунок 4. Пример перечисления разрезов | ||
Лемма 1. После не более чем Kn итераций процедура перечисления разрезов найдет K-разрезы для всех вершин в N. | ''Лемма 1. После не более чем Kn итераций процедура перечисления разрезов найдет K-разрезы для всех вершин в N.'' | ||
В работе [7] были предложены некоторые техники для ускорения | В работе [7] были предложены некоторые техники для ускорения выполнения процедуры. С их помощью все 4-разрезы для каждой из эталонных схем ISCAS89 могут быть найдены не более чем за пять итераций. | ||
'''Этап разметки''' | '''Этап разметки''' | ||
После получения всех K-разрезов алгоритм оценивает разрезы, основываясь на последовательном времени прихода (или l-значениях), представляющем собой расширение традиционного времени прихода, чтобы рассчитать эффект от ресинхронизации [6, 8]. | |||
'''FindMinLabels'''(N) | |||
'''foreach''' вершины v в N '''do''' <math>l(v) \Leftarrow -w_v \cdot \phi</math> | |||
'''while''' (имеются обновления меток) '''do''' | |||
'''foreach''' вершины v в N '''do''' | |||
<math>l(v) \Leftarrow min_{c \in C} \{ max \{ l(u) - d \cdot \phi + 1 | u^d \in c \} \} </math> | |||
'''if''' v является первичным выходом и <math>l(v) > \phi</math>, '''return''' «Неуспешно» | |||
'''return''' «Успешно» | |||
Рисунок 5. Процедура разметки | |||
{| class="wikitable" style="text-align:center" | |||
|- | |||
! Итер. !! a !! b !! i !! x !! y !! z !! o | |||
|- | |||
! 0 | |||
| <math>\{ a^0 \}: 0</math> || <math>\{ b^0 \}: 0</math> || <math>\{ i^0 \}: 0</math> || <math>\{ x^0 \}: -1</math> || <math>\{ y^0 \}: 0</math> || <math>\{ z^0 \}: -1</math> || <math>\{ o^0 \}: -1</math> | |||
|- | |||
! 1 | |||
| || || <math>\{ a^0 \}: 1</math> | |||
|| <math>\{ a^1, z^1 \}: 0</math> | |||
|| <math>\{ a^0, b^0, z^0 \}: 1</math> | |||
|| <math>\{ a^1, z^1, b^1 \}: 0</math> | |||
|| <math>\{ z^0 \}: 0</math> | |||
|} | |||
Рисунок 6. Пример разметки | |||
Процедура разметки стремится найти метку для каждой вершины, как схематически показано на рис. 5, где <math>w_v</math> обозначает вес кратчайших путей из первичных входов к вершине v. | |||
На рис. 6 изображены итерации вычисления меток для схемы на рис. 1 (1) в предположении, что целевая продолжительность цикла <math>\phi = 1</math> и вершины оцениваются в порядке i, x, y, z, o. В таблице отражены как текущая метка, так и соответствующий разрез для каждой вершины. В данном примере после первой итерации ни одна из меток не меняется, и выполнение процедуры завершается. | |||
Можно показать, что процедура разметки остановится после не более чем n(n - 1) итераций [9]. Следующая лемма связывает метки и отображение: | |||
''Лемма 2. N имеет отображение с продолжительностью цикла <math>\varphi</math> в том и только том случае, если процедура разметки возвращает значение «Успешно».'' | |||
'''Этап отображения''' | |||
После успешного вычисления меток для всех вершин можно построить отображение, начиная с первичных выходов. В каждой вершине v процедура выбирает разрез, реализующий метку вершины, а затем переходит к выбору разреза для u, если <math>u^d</math> входит в состав разреза, выбранного для v. На ребре, идущем из таблицы LUT для u к LUT для v, добавляется d триггеров. Для схемы на рис. 1 (1) сгенерированное отображение, основанное на метках, найденных на рис. 6, представляет собой сеть на рис. 2 (2). | |||
Для получения отображения с целевой продолжительностью цикла <math>\varphi</math> таблица LUT для v может быть ресинхронизирована на <math>\lceil l(v) / \phi \rceil - 1</math>. Для схемы на рис. 1 (1) окончательное отображение после ресинхронизации представлено на рис. 2 (3). | |||
== Применение == | |||
Данный алгоритм может применяться для отображения технологически независимой булевой сети на сеть, состоящую из ячеек из библиотеки логических элементов целевой технологии. Концепция и структура являются достаточно общими для того, чтобы их можно было адаптировать для изучения других оптимизаций схем, таких как кластеризация и реструктуризация последовательных схем. | |||
== См. также == | |||
* [[Ресинхронизация схемы]] | |||
* [[Технологическое отображение ППВМ]] | |||
* [[Технологическое отображение]] | |||
== Литература == | |||
1. Cong, J., Ding, Y.: FlowMap: An Optimal Technology Mapping Algorithm for Delay Optimization in Lookup-Table Based FPGA Designs. IEEE Trans. on Comput. Aided Des. of Integr. Circuits and Syst., 13(1), 1-12(1994) | |||
2. Cong, J., Wu, C.: FPGA Synthesis with Retiming and Pipelining for Clock Period Minimization of Sequential Circuits. ACM/IEEE Design Automation Conference (1997) | |||
3. Keutzer, K.: DAGON: Technology Binding and Local Optimization by DAG Matching. ACM/IEEE Design Automation Conference (1987) | |||
4. Leiserson, C.E., Saxe, J.B.: Retiming Synchronous Circuitry. Algorithmica6,5-35(1991) | |||
5. Mishchenko, A., Chatterjee, S., Brayton, R., Ciesielski, M.: An integrated technology mapping environment. International Workshop on Logic Synthesis (2005) | |||
6. Pan, P.: Continuous Retiming: Algorithms and Applications. IEEE International Conference on Computer Design, pp. 116-121. (1997) | |||
7. Pan, P., Lin, C.C.: A New Retiming-based Technology Mapping Algorithm for LUT-based FPGAs. ACM International Symposium on Field-Programmable Gate Arrays (1998) | |||
8. Pan, P., Liu, C.L.: Optimal Clock Period FPGA Technology Mapping for Sequential Circuits. ACM/IEEE Design Automation Conference, June (1996) | |||
9. Pan, P., Liu, C.L.: Optimal Clock Period FPGA Technology Mapping for Sequential Circuits. ACM Trans. on Des. Autom. of Electron. Syst., 3(3), 437-462 (1998) | |||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 04:18, 7 декабря 2024
Ключевые слова и синонимы
Интегрированные ресинхронизация и технологическое отображение; технологическое отображение с ресинхронизацией
Постановка задачи
Одним из ключевых этапов процесса проектирования СБИС является технологическое отображение, которое преобразует булеву сеть, состоящую из технологически инвариантных логических вентилей и D-триггеров, тактируемых перепадом напряжения (FF), в эквивалентную сеть, состоящую из ячеек из библиотеки логических элементов целевой технологии [1, 3, 5]. Технологическое отображение может быть сформулировано как задача покрытия, в которой осуществляется покрытие логических вентилей элементами технологической библиотеки. Для простоты изложения предположим, что библиотека содержит только один элемент – таблицу поиска с K логическими входами (K-LUT) с единичной задержкой. Таблица K-LUT может реализовать любую булеву функцию с не более чем K входами, как в случае с высокоэффективными программируемыми пользователем вентильными матрицами (ППВМ).
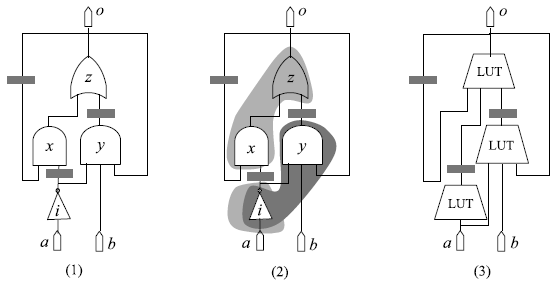
Пример технологического отображения приведен на рис. 1. Для исходной сети на схеме (1) с тремя триггерами и четырьмя вентилями строится покрытие тремя 3-входовыми конусами, как показано на рис. 1 (2). Соответствующее отображение с использованием таблиц 3-LUT показано на рис. 1 (3). Заметим, что вентиль i покрывается двумя конусами. У отображения на рис. 1 (3) продолжительность цикла (или период цикла) составляет две единицы, что равняется совокупной задержке на самом длинном пути между триггерами (FF), от первичных входов (PI) до триггеров и от триггеров до первичных выходов (PO).
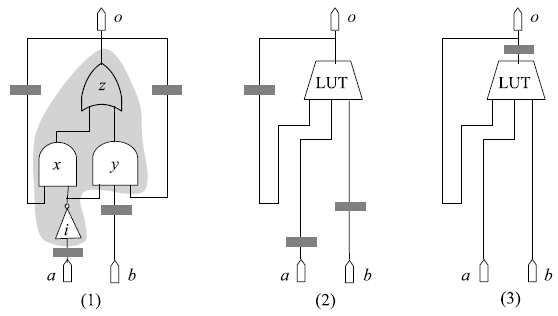
Ресинхронизация представляет собой преобразование, которое перемещает триггервы по схеме, сохраняя ее функциональность [4]. Она может повлиять на технологическое отображение. На рис. 2 (1) представлена схема, полученная из схемы на рис. 1 (1) в результате ресинхронизации триггеров на выходах y и i к их входам. Эта схема может быть покрыта всего одним 3-входовым конусом, как показано на рис. 2 (1). Соответствующее отображение, представленное на рис. 2 (2), как с точки зрения синхронизации, так и с точки зрения площади, лучше функционально эквивалентного первого решения на рис. 1 (3), полученного без ресинхронизации.
Рисунок 1. Технологическое отображение: (1) исходная сеть, (2) покрытие, (3) отображение
Рисунок 2. Ресинхронизация и отображение: (1) ресинхронизация и покрытие, (2) отображение, (3) решение после ресинхронизации
K-ограниченной сетью называется сеть, в которой каждый вентиль имеет не более K входов. Задачу технологического отображения последовательной схемы можно определить следующим образом. Пусть даны K-ограниченная булева сеть N и целевая продолжительность цикла [math]\displaystyle{ \varphi }[/math]. Найти отображение с продолжительностью цикла [math]\displaystyle{ \varphi }[/math], предполагая, что допускается перемещение триггеров при помощи ресинхронизации.
Основные результаты
Первый алгоритм с полиномиальным временем выполнения для этой задачи был предложен в работах [8, 9]. Улучшенный алгоритм в работе [2] обеспечивал сокращение времени выполнения. Оба этих алгоритма были основаны на вычислении потока с минимальной стоимостью.
В работе [7] был представлен другой алгоритм, который использовал преимущество знания того факта, что на практике K является небольшим целым числом, обычно от 3 до 6. Алгоритм выполняет перечисление всех K-входовых конусов для каждого вентиля. Он может учитывать другие целевые показатели оптимизации (например, площадь и мощность) и может применяться к стандартным библиотекам логических элементов.
Перечисление разрезов
Булева сеть может быть представлена в виде ориентированного графа со взвешенными ребрами, вершинами которого являются логические вентили, первичные входы и первичные выходы. В нем имеется ориентированное ребро (u, v) с весом d, если u, после прохода через d триггеров, воздействует на v.
Логический конус для вершины может быть представлен в виде разреза, состоящего из входов конуса. Элемент разреза для v состоит из задающей вершины u и суммарного веса d на путях из u в v, обозначаемого [math]\displaystyle{ u^d }[/math]. Если u достигает v по нескольким путям с разным числом триггеров, u будет входить в разрез несколько раз с разными значениями d. К примеру, для конуса для z на рис 2 (2) соответствующий разрез будет иметь вид [math]\displaystyle{ \{ z^1, a^1, b^1 \} }[/math]. Разрез размера K называется K-разрезом.
Пусть [math]\displaystyle{ (u_i, v) }[/math] – ребро в N с весом [math]\displaystyle{ d_i }[/math], а [math]\displaystyle{ C(u_i) }[/math] – множество K-разрезов для [math]\displaystyle{ d_i }[/math], i = 1, ..., t. Обозначим за [math]\displaystyle{ merge(C(u_1), ..., C(u_t)) }[/math] следующую операцию на множествах:
[math]\displaystyle{ \{ \{ v^0 \} \} \cup \{ c^{d_1}_1 \cup ... \cup c^{d_t}_t | c_1 \in C(u_1), ..., c_t \in C(u_t), | c^{d_1}_1 \cup ... \cup c^{d_t}_t | \le K \} }[/math],
где [math]\displaystyle{ c^{d_i}_i = \{ u^{d + d_i} | u^d \in c_i \} }[/math] для i = 1, ..., t. Очевидно, что [math]\displaystyle{ merge(C(u_1), ..., C(u_t)) }[/math] является множеством K-разрезов для v.
Если в сети N не имеется циклов, K-разрезы для всех вершин можно определить при помощи операции слияния merge в топологическом порядке, начиная с первичных входов. Для сетей общего вида на рис. 3 представлена процедура итеративного вычисления разрезов, предложенная в работе [7].
На рис. 4 изображены итерации перечисления 3-разрезов для схемы на рис. 1 (1) при слиянии разрезов в порядке i, x, y, z, o. В начале работы каждая вершина имеет собственный тривиальный разрез, включающий ее саму. В ряду 1 представлены новые разрезы, обнаруженные на первой итерации. На второй итерации обнаруживаются еще два новых разреза (для x). После этого выполнение процедуры останавливается, так как последующие слияния не приводят к выявлению новых разрезов.
FindAllCuts(N, K) foreach вершины v в N do [math]\displaystyle{ C(v) \Leftarrow \{ \{ v^0 \} \} }[/math] while (находятся новые разрезы) do foreach вершины v в N do [math]\displaystyle{ C(v) \Leftarrow merge(C(u_1), ..., C(u_t)) }[/math]
Рисунок 3. Процедура перечисления разрезов
| Итер. | a | b | i | x | y | z | o |
|---|---|---|---|---|---|---|---|
| 0 | [math]\displaystyle{ \{ a^0 \} }[/math] | [math]\displaystyle{ \{ b^0 \} }[/math] | [math]\displaystyle{ \{ i^0 \} }[/math] | [math]\displaystyle{ \{ x^0 \} }[/math] | [math]\displaystyle{ \{ y^0 \} }[/math] | [math]\displaystyle{ \{ z^0 \} }[/math] | [math]\displaystyle{ \{ o^0 \} }[/math] |
| 1 | [math]\displaystyle{ \{ a^0 \} }[/math] | [math]\displaystyle{ \{ i^1, z^1 \} }[/math]
[math]\displaystyle{ \{ a^1, z^1 \} }[/math] |
[math]\displaystyle{ \{ i^0, b^0, z^0 \} }[/math]
[math]\displaystyle{ \{ a^0, b^0, z^0 \} }[/math] |
[math]\displaystyle{ \{ x^0, y^1 \} }[/math] [math]\displaystyle{ \{ i^1, z^1, b^1 \} }[/math] [math]\displaystyle{ \{ a^1, z^1, b^1 \} }[/math] [math]\displaystyle{ \{ i^1, z^1, y^1 \} }[/math] [math]\displaystyle{ \{ a^1, z^1, y^1 \} }[/math] |
[math]\displaystyle{ \{ z^0 \} }[/math] | ||
| 2 | [math]\displaystyle{ \{ i^1, x^1, y^2 \} }[/math]
[math]\displaystyle{ \{ a^1, x^1, y^2 \} }[/math] |
Рисунок 4. Пример перечисления разрезов
Лемма 1. После не более чем Kn итераций процедура перечисления разрезов найдет K-разрезы для всех вершин в N.
В работе [7] были предложены некоторые техники для ускорения выполнения процедуры. С их помощью все 4-разрезы для каждой из эталонных схем ISCAS89 могут быть найдены не более чем за пять итераций.
Этап разметки
После получения всех K-разрезов алгоритм оценивает разрезы, основываясь на последовательном времени прихода (или l-значениях), представляющем собой расширение традиционного времени прихода, чтобы рассчитать эффект от ресинхронизации [6, 8].
FindMinLabels(N)
foreach вершины v в N do [math]\displaystyle{ l(v) \Leftarrow -w_v \cdot \phi }[/math]
while (имеются обновления меток) do
foreach вершины v в N do
[math]\displaystyle{ l(v) \Leftarrow min_{c \in C} \{ max \{ l(u) - d \cdot \phi + 1 | u^d \in c \} \} }[/math]
if v является первичным выходом и [math]\displaystyle{ l(v) \gt \phi }[/math], return «Неуспешно»
return «Успешно»
Рисунок 5. Процедура разметки
| Итер. | a | b | i | x | y | z | o |
|---|---|---|---|---|---|---|---|
| 0 | [math]\displaystyle{ \{ a^0 \}: 0 }[/math] | [math]\displaystyle{ \{ b^0 \}: 0 }[/math] | [math]\displaystyle{ \{ i^0 \}: 0 }[/math] | [math]\displaystyle{ \{ x^0 \}: -1 }[/math] | [math]\displaystyle{ \{ y^0 \}: 0 }[/math] | [math]\displaystyle{ \{ z^0 \}: -1 }[/math] | [math]\displaystyle{ \{ o^0 \}: -1 }[/math] |
| 1 | [math]\displaystyle{ \{ a^0 \}: 1 }[/math] | [math]\displaystyle{ \{ a^1, z^1 \}: 0 }[/math] | [math]\displaystyle{ \{ a^0, b^0, z^0 \}: 1 }[/math] | [math]\displaystyle{ \{ a^1, z^1, b^1 \}: 0 }[/math] | [math]\displaystyle{ \{ z^0 \}: 0 }[/math] |
Рисунок 6. Пример разметки
Процедура разметки стремится найти метку для каждой вершины, как схематически показано на рис. 5, где [math]\displaystyle{ w_v }[/math] обозначает вес кратчайших путей из первичных входов к вершине v.
На рис. 6 изображены итерации вычисления меток для схемы на рис. 1 (1) в предположении, что целевая продолжительность цикла [math]\displaystyle{ \phi = 1 }[/math] и вершины оцениваются в порядке i, x, y, z, o. В таблице отражены как текущая метка, так и соответствующий разрез для каждой вершины. В данном примере после первой итерации ни одна из меток не меняется, и выполнение процедуры завершается.
Можно показать, что процедура разметки остановится после не более чем n(n - 1) итераций [9]. Следующая лемма связывает метки и отображение:
Лемма 2. N имеет отображение с продолжительностью цикла [math]\displaystyle{ \varphi }[/math] в том и только том случае, если процедура разметки возвращает значение «Успешно».
Этап отображения
После успешного вычисления меток для всех вершин можно построить отображение, начиная с первичных выходов. В каждой вершине v процедура выбирает разрез, реализующий метку вершины, а затем переходит к выбору разреза для u, если [math]\displaystyle{ u^d }[/math] входит в состав разреза, выбранного для v. На ребре, идущем из таблицы LUT для u к LUT для v, добавляется d триггеров. Для схемы на рис. 1 (1) сгенерированное отображение, основанное на метках, найденных на рис. 6, представляет собой сеть на рис. 2 (2).
Для получения отображения с целевой продолжительностью цикла [math]\displaystyle{ \varphi }[/math] таблица LUT для v может быть ресинхронизирована на [math]\displaystyle{ \lceil l(v) / \phi \rceil - 1 }[/math]. Для схемы на рис. 1 (1) окончательное отображение после ресинхронизации представлено на рис. 2 (3).
Применение
Данный алгоритм может применяться для отображения технологически независимой булевой сети на сеть, состоящую из ячеек из библиотеки логических элементов целевой технологии. Концепция и структура являются достаточно общими для того, чтобы их можно было адаптировать для изучения других оптимизаций схем, таких как кластеризация и реструктуризация последовательных схем.
См. также
Литература
1. Cong, J., Ding, Y.: FlowMap: An Optimal Technology Mapping Algorithm for Delay Optimization in Lookup-Table Based FPGA Designs. IEEE Trans. on Comput. Aided Des. of Integr. Circuits and Syst., 13(1), 1-12(1994)
2. Cong, J., Wu, C.: FPGA Synthesis with Retiming and Pipelining for Clock Period Minimization of Sequential Circuits. ACM/IEEE Design Automation Conference (1997)
3. Keutzer, K.: DAGON: Technology Binding and Local Optimization by DAG Matching. ACM/IEEE Design Automation Conference (1987)
4. Leiserson, C.E., Saxe, J.B.: Retiming Synchronous Circuitry. Algorithmica6,5-35(1991)
5. Mishchenko, A., Chatterjee, S., Brayton, R., Ciesielski, M.: An integrated technology mapping environment. International Workshop on Logic Synthesis (2005)
6. Pan, P.: Continuous Retiming: Algorithms and Applications. IEEE International Conference on Computer Design, pp. 116-121. (1997)
7. Pan, P., Lin, C.C.: A New Retiming-based Technology Mapping Algorithm for LUT-based FPGAs. ACM International Symposium on Field-Programmable Gate Arrays (1998)
8. Pan, P., Liu, C.L.: Optimal Clock Period FPGA Technology Mapping for Sequential Circuits. ACM/IEEE Design Automation Conference, June (1996)
9. Pan, P., Liu, C.L.: Optimal Clock Period FPGA Technology Mapping for Sequential Circuits. ACM Trans. on Des. Autom. of Electron. Syst., 3(3), 437-462 (1998)