Модель без явного задания параметров кэша: различия между версиями
Irina (обсуждение | вклад) |
KVN (обсуждение | вклад) |
||
| (не показаны 2 промежуточные версии 1 участника) | |||
| Строка 51: | Строка 51: | ||
При выполнении поиска B-деревья обеспечивают стоимость O( | При выполнении поиска B-деревья обеспечивают стоимость <math>O(log_B \; N)</math>, что является оптимальным в модели ввода-вывода для поиска на базе сравнения. Эта стоимость достижима и в модели без явного задания параметров кэша, что было показано для статического [25] и для динамического случая [13]. Позднее было предложено несколько вариантов деревьев поиска без явного задания параметров кэша. Кроме того, в [12] было показано различие между алгоритмами без явного задания параметров кэша и алгоритмами модели ввода-вывода, а именно – что константы, достижимые в границе <math>O(log_B \; N)</math>, доказуемо различаются. | ||
Перестановка в модели ввода-вывода имеет сложность | Перестановка в модели ввода-вывода имеет сложность <math>\Theta (min \{ Sort(N), N \} ) \;</math> в предположении, что элементы неделимы [2]. Было доказано [16], что эта асимптотическая сложность не может быть получена в модели без явного задания параметров кэша, так что и в случае этой задачи разделение имеет место. | ||
Была предложена реализация очередей с приоритетами на базе модели без явного задания параметров кэша с <math>O(\frac{1}{B} log_{\frac{M}{B}} \; \frac{N}{M})</math> амортизированных переносов содержимого памяти. | |||
К настоящему времени также разработаны алгоритмы модели без явного задания параметров кэша для задач вычислительной геометрии [1, 6, 7, 8, 10, 15], графовых задач [4, 17, 18, 23], для сканирования динамических множеств [ ], укладки статических деревьев [11], задач поиска на мультимножествах [21], динамического программирования [19], частичной устойчивости [10], матричных операций [22] и быстрого преобразования Фурье [22]. | |||
К настоящему времени также разработаны алгоритмы модели без явного задания параметров кэша для задач вычислительной геометрии [1, 6, 7, 8, 10, 15], графовых задач [4, 17, 18, 23], для сканирования динамических множеств [9], укладки статических деревьев [11], задач поиска на мультимножествах [21], динамического программирования [19], частичной устойчивости [10], матричных операций [22] и быстрого преобразования Фурье [22]. | |||
== Применение == | == Применение == | ||
| Строка 125: | Строка 126: | ||
27. Vitter, J.S.: Geometric and spatial data structures in external memory. In: Mehta, D., Sahni, S. (eds.) Handbook on Data Structures and Applications. CRC Press, Boca Raton (2005) | 27. Vitter, J.S.: Geometric and spatial data structures in external memory. In: Mehta, D., Sahni, S. (eds.) Handbook on Data Structures and Applications. CRC Press, Boca Raton (2005) | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 03:57, 7 декабря 2024
Определение модели
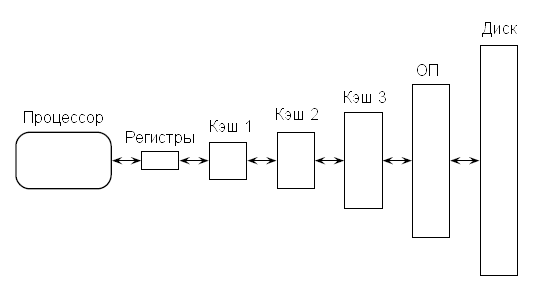
Система памяти современного компьютера включает несколько иерархических уровней, каждый из которых выступает в качестве кэша для следующего; типичная иерархия может состоять из регистров, кэша 1 уровня, кэша 2 уровня, кэша 3 уровня, основной памяти и дисковой памяти (рис. 1). Одна из характеристик иерархии заключается в том, что уровни памяти становятся больше и медленнее по мере удаления от процессора; разница в скорости доступа оказывается самой масштабной при переходе от оперативной памяти (RAM) к дисковой. Еще одно свойство заключается в том, что данные перемещаются между уровнями в виде блоков.
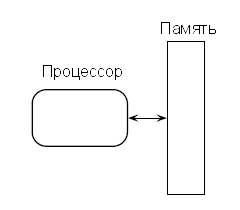
Разница в скорости доступа между уровнями приводит к тому, что стоимость обращений к памяти в значительной мере зависит от того, на каким самом внутреннем уровне памяти находится нужный элемент. Таким образом, схема обращений к памяти некоторого алгоритма в значительной мере определяет время его выполнения на практике. К сожалению, RAM-модель (рис. 2), традиционно используемая для разработки и анализа алгоритмов, не отражает этого, поскольку предполагает, что все обращения к памяти занимают одинаковое время.
Рис. 1. Иерархия памяти
Рис. 2. RAM-модель
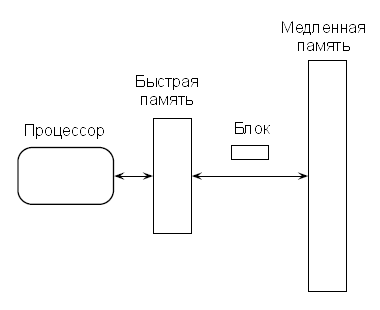
Для более адекватного отражения влияния иерархии памяти было разработано несколько вычислительных моделей. Самая простая и успешная из них – двухуровневая модель ввода-вывода, предложенная Аггарвалом и Виттером [2] (рис. 3). В этой модели используется двухуровневая иерархия памяти, состоящей из быстрой памяти размера M и более медленной памяти неограниченного размера, при этом перенос данных между уровнями осуществляется блоками по B последовательных элементов. Вычисления могут выполняться только над данными в быстрой памяти. Предполагается, что алгоритмы полностью контролируют перенос блоков между двумя уровнями. Этот процесс будет называться переносом содержимого памяти. Мерой сложности является количество выполненных переносов содержимого памяти. Преимущество модели ввода-вывода заключается в том, что она частично отражает иерархию памяти и при этом достаточно проста, чтобы на ее основе можно было выполнять разработку и анализ алгоритмов. За последние двадцать лет было получено множество результатов применения модели ввода-вывода, охватывающих большинство областей теории алгоритмов. Довольно полное представление можно получить в обзорах [3, 24, 26, 27].
Рис. 3. Модель ввода-вывода
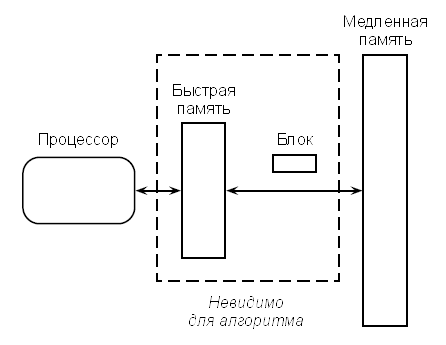
Рис. 4. Модель без явного задания параметров кэша
Были также предложены более замысловатые модели многоуровневой памяти (см. обзор в [26]), однако они оказались менее успешными – главным образом из-за их сложности, затрудняющей анализ алгоритмов. Все эти модели, включая модель ввода-вывода, предполагают, что характеристики иерархии памяти (уровень и размер блоков) заранее известны.
Модель памяти без явного задания параметров кэша (рис. 4) была предложена в 1999 году Фриго и др. [22]. Алгоритм без явного задания параметров кэша представляет собой алгоритм, формулируемый в рамках RAM-модели, но анализируемый в рамках модели ввода-вывода, причем анализ должен быть действительным при любых значениях размера блока B и размера памяти M. Предполагается, что перенос содержимого памяти выполняется автоматически при помощи оптимальной автономной стратегии замещения кэша.
Главное достоинство модели ввода-вывода заключается в следующем: в силу того, что анализ в рамках модели ввода-вывода действителен при любых значениях размера блока и размера памяти, он оказывается верен для всех уровней многоуровневой иерархии памяти (детальное обоснование этого утверждения см. в [22, 25]). Иначе говоря, если оптимизировать алгоритм на одном, неизвестном, уровне иерархии, он будет одновременно оптимизирован на всех уровнях. Таким образом, модель без явного задания параметров кэша изящно обобщает модель ввода-вывода до модели многоуровневой памяти за счет одного простого условия: алгоритму не позволено знать значения B и M. Задача заключается в разработке алгоритмов, демонстрирующих при этих условиях наилучшее значение количества переносов.
Помимо концептуально простого отображения всей иерархии памяти, модель без явного задания параметров кэша также имеет и другие преимущества. Алгоритмы, разработанные на основе этой модели, не полагаются на знание параметров иерархии памяти; это может пригодиться, например, при разработке программ, которые будут работать на различных или неизвестных архитектурах (таких как библиотечные программы или программы для гетерогенных распределенных вычислений – например, сетевых коллективных вычислений и проектов наподобие SETI@home). Даже на единственной и известной архитектуре параметры памяти, доступные вычислительному процессу, могут быть непостоянными, если несколько процессов конкурируют за одни и те же ресурсы памяти. Поскольку алгоритмы без явного задания параметров кэша оптимизированы для всех значений параметров, они потенциально способны лучше адаптироваться к подобным изменениям, а также к различным размерам входных данных, вынуждающих использовать различные уровни памяти. Наконец, алгоритмы без явного задания параметров кэша автоматически оптимизируют использование буферов динамической трансляции (кэша, содержащего недавно посещенные части таблицы страниц, используемого для виртуальной памяти) процессора, что можно рассматривать как вторую иерархию памяти, параллельную упомянутой в начале обзора.
Возможными слабыми местами модели без явного задания параметров кэша являются предположение об оптимальности автономной стратегии замещения кэша и отсутствие моделирования ограниченной ассоциативности многих уровней иерархии. Первое обстоятельство смягчается тем фактом, что обычно имеющийся анализ алгоритма без явного задания параметров кэша так же хорош в случае замещения кэша при помощи политики замещения наиболее давно использовавшегося элемента, что довольно близко к фактически используемым в компьютерах стратегиях. Второе обстоятельство является слабым местом и многих других моделей памяти.
Основные результаты
Далее будет приведен краткий обзор известных результатов для модели без явного задания параметров кэша. Также заслуживают внимания обзоры в работах [5, 14, 20, 24].
Прежде всего, отметим, что сканирование массива из N элементов требует O(N/B) переносов содержимого памяти для любых значений B и M и, следовательно, является оптимальным алгоритмом без явного задания параметров кэша. Таким образом, стандартные RAM-алгоритмы, основанные на сканировании, могут уже демонстрировать хорошие показатели при использовании модели без явного задания параметров кэша – например, классический детерминированный алгоритм выбора имеет сложность O(N/B) [20].
Что касается сортировки, то фундаментальной особенностью модели ввода-вывода является то, что сортировка N элементов при помощи сравнения требует [math]\displaystyle{ \Theta (Sort(N)) \; }[/math] переносов содержимого памяти [2], где [math]\displaystyle{ Sort(N) = \frac{N}{B} log_{\frac{M}{B}} \; \frac{N}{M} }[/math]. В модели без явного задания параметров кэша сортировка может быть выполнена за [math]\displaystyle{ \Theta (Sort(N)) \; }[/math] переносов содержимого памяти при условии принятия так называемого предположения о высоте кэша – [math]\displaystyle{ M \ge B^{1 + \varepsilon} \; }[/math] [15,22]. Было показано, что выполнение этого предположения обязательно [16], что доказывает разницу в эффективности между алгоритмами без явного задания параметров кэша и алгоритмами в модели ввода-вывода (где это предположение не требуется для определения границы сортировки).
При выполнении поиска B-деревья обеспечивают стоимость [math]\displaystyle{ O(log_B \; N) }[/math], что является оптимальным в модели ввода-вывода для поиска на базе сравнения. Эта стоимость достижима и в модели без явного задания параметров кэша, что было показано для статического [25] и для динамического случая [13]. Позднее было предложено несколько вариантов деревьев поиска без явного задания параметров кэша. Кроме того, в [12] было показано различие между алгоритмами без явного задания параметров кэша и алгоритмами модели ввода-вывода, а именно – что константы, достижимые в границе [math]\displaystyle{ O(log_B \; N) }[/math], доказуемо различаются.
Перестановка в модели ввода-вывода имеет сложность [math]\displaystyle{ \Theta (min \{ Sort(N), N \} ) \; }[/math] в предположении, что элементы неделимы [2]. Было доказано [16], что эта асимптотическая сложность не может быть получена в модели без явного задания параметров кэша, так что и в случае этой задачи разделение имеет место.
Была предложена реализация очередей с приоритетами на базе модели без явного задания параметров кэша с [math]\displaystyle{ O(\frac{1}{B} log_{\frac{M}{B}} \; \frac{N}{M}) }[/math] амортизированных переносов содержимого памяти.
К настоящему времени также разработаны алгоритмы модели без явного задания параметров кэша для задач вычислительной геометрии [1, 6, 7, 8, 10, 15], графовых задач [4, 17, 18, 23], для сканирования динамических множеств [9], укладки статических деревьев [11], задач поиска на мультимножествах [21], динамического программирования [19], частичной устойчивости [10], матричных операций [22] и быстрого преобразования Фурье [22].
Применение
Модель без явного задания параметров кэша предтавляет собой инструмент разработки и анализа алгоритмов, эффективно использующий иерархию памяти компьютеров.
Экспериментальные результаты
Алгоритмы без явного задания параметров кэша эмпирически оценивались в множестве областей, включая сортировку, поиск, матричные алгоритмы [22] и динамическое программирование [19]. На основании этих оценок можно сделать вывод, что методы без явного задания параметров кэша нередко превосходят по эффективности RAM-алгоритмы, хотя иногда не в такой степени, как алгоритмы, специально приспособленные для конкретной иерархии памяти и размера задачи. С другой стороны, алгоритмы без явного задания параметров кэша хорошо работают на всех уровнях иерархии памяти, а также более устойчивы к изменению размеров задач.
См. также
- B-деревья без явного задания параметров кэша
- Сортировка без явного задания параметров кэша
- Модель ввода-вывода
Литература
1. Agarwal, P.K., Arge, L., Danner, A., Holland-Minkley, B.: Cache-oblivious data structures for orthogonal range searching. In: Proc. 19th ACM Symposium on Computational Geometry, pp. 237-245. ACM, New York (2003)
2. Aggarwal, A., Vitter, J.S.: The Input/Output complexity of sorting and related problems. Commun. ACM 31(9), 1116-1127 (1988)
3. Arge, L.: External memory data structures. In: Abello, J., Pardalos, P.M., Resende, M.G.C. (eds.) Handbook of Massive Data Sets, pp. 313-358. Kluwer Academic Publishers, Boston (2002)
4. Arge, L., Bender, M.A., Demaine, E.D., Holland-Minkley, B., Munro, J.I.: Cache-oblivious priority queue and graph algorithm applications. In: Proc. 34th Annual ACM Symposium on Theory of Computing, pp. 268-276. ACM, New York (2002)
5. Arge, L., Brodal, G.S., Fagerberg, R.: Cache-oblivious data structures. In: Mehta, D., Sahni, S. (eds.) Handbook on Data Structures and Applications. CRC Press, Boca Raton (2005)
6. Arge, L., Brodal, G.S., Fagerberg, R., Laustsen, M.: Cache-oblivious planar orthogonal range searching and counting. In: Proc. 21st Annual ACM Symposium on Computational Geometry, pp. 160-169. ACM, New York (2005)
7. Arge, L.,de Berg, M., Haverkort, H.J.: Cache-oblivious R-trees. In: Symposium on Computational Geometry, pp. 170-179. ACM, New York (2005)
8. Arge, L., Zeh, N.: Simple and semi-dynamic structures for cache-oblivious planar orthogonal range searching. In: Symposium on Computational Geometry, pp. 158-166. ACM, New York (2006)
9. Bender, M., Cole, R., Demaine, E., Farach-Colton, M.: Scanning and traversing: Maintaining data for traversals in a memory hierarchy. In: Proc. 10th Annual European Symposium on Algorithms. LNCS, vol. 2461, pp. 139-151. Springer, Berlin (2002)
10. Bender, M., Cole, R., Raman, R.: Exponential structures for cache-oblivious algorithms. In: Proc. 29th International Colloquium on Automata, Languages, and Programming. LNCS, vol. 2380, pp. 195-207. Springer, Berlin (2002)
11. Bender, M., Demaine, E., Farach-Colton, M.: Efficient tree layoutin a multilevel memory hierarchy. In: Proc. 10th Annual European Symposium on Algorithms.LNCS, vol.2461, pp. 165-173. Springer, Berlin (2002). Full version at http://arxiv.org/abs/cs/0211010
12. Bender, M.A., Brodal, G.S., Fagerberg, R., Ge, D., He, S., Hu, H., Iacono, J., Lopez-Ortiz, A.: The cost of cache-oblivious searching. In: Proc. 44th Annual IEEE Symposium on Foundations of Computer Science, pp. 271-282. IEEE Computer Society Press, Los Alamitos (2003)
13. Bender, M.A., Demaine, E.D., Farach-Colton, M.: Cache-oblivious B-trees. In: 41st Annual Symposium on Foundations of Computer Science, pp. 399-409. IEEE Computer Society Press, Los Alamitos (2000)
14. Brodal, G.S.: Cache-oblivious algorithms and data structures. In: Proc. 9th Scandinavian Workshop on Algorithm Theory. LNCS, vol. 3111, pp. 3-13. Springer, Berlin (2004)
15. Brodal, G.S., Fagerberg, R.: Cache oblivious distribution sweeping. In: Proc. 29th International Colloquium on Automata, Languages, and Programming. LNCS, vol. 2380, pp. 426-438. Springer, Berlin (2002)
16. Brodal, G.S., Fagerberg, R.: On the limits of cache-obliviousness. In: Proc. 35th Annual ACM Symposium on Theory of Computing, pp. 307-315. ACM, New York (2003)
17. Brodal, G.S., Fagerberg, R., Meyer, U., Zeh, N.: Cache-oblivious data structures and algorithms for undirected breadth-first search and shortest paths. In: Proc. 9th Scandinavian Workshop on Algorithm Theory. LNCS, vol. 3111, pp. 480-492. Springer, Berlin (2004)
18. Chowdhury, R.A., Ramachandran, V.: Cache-oblivious shortest paths in graphs using buffer heap. In: Proc. 16th Annual ACM Symposium on Parallelism in Algorithms and Architectures. ACM, New York (2004)
19. Chowdhury, R.A., Ramachandran, V.: Cache-oblivious dynamic programming. In: Proc. 17th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 591-600. ACM-SIAM, New York (2006)
20. Demaine, E.D.: Cache-oblivious algorithms and data structures. In: Proc. EFF summer school on massive data sets, LNCS. Springer, Berlin. To appear. Online version at http://theory.csail.mit.edu/edemaine/papers/BRICS2002/
21. Farzan, A., Ferragina, P., Franceschini, G., Munro, J.I.: Cache-oblivious comparison-based algorithms on multisets. In: Proc. 13th Annual European Symposium on Algorithms. LNCS, vol. 3669, pp. 305-316. Springer, Berlin (2005)
22. Frigo, M., Leiserson, C.E., Prokop, H., Ramachandran, S.: Cache-oblivious algorithms. In: 40th Annual IEEE Symposium on Foundations of Computer Science, pp. 285-298. IEEE Computer Society Press, Los Alamitos (1999)
23. Jampala, H., Zeh, N.: Cache-oblivious planar shortest paths. In: Proc. 32nd International Colloquium on Automata, Languages, and Programming. LNCS, vol. 3580, pp. 563-575. Springer, Berlin (2005)
24. Meyer, U., Sanders, P., Sibeyn, J.F. (eds.): Algorithms for Memory Hierarchies. LNCS, vol. 2625. Springer, Berlin (2003)
25. Prokop, H.: Cache-oblivious algorithms. Master's thesis, Massachusetts Institute of Technology, Dept. of Electrical Engineering and Computer Science (1999)
26. Vitter, J.S.: External memory algorithms and data structures: Dealing with MASSIVE data. ACM Comput. Surv. 33(2), 209-271 (2001)
27. Vitter, J.S.: Geometric and spatial data structures in external memory. In: Mehta, D., Sahni, S. (eds.) Handbook on Data Structures and Applications. CRC Press, Boca Raton (2005)