Сортировка без явного задания параметров кэша: различия между версиями
Irina (обсуждение | вклад) |
KVN (обсуждение | вклад) |
||
| (не показано 8 промежуточных версий 1 участника) | |||
| Строка 19: | Строка 19: | ||
''Бинарная сортировка слиянием (Mergesort)'' выполняет <math>O(N \; log_2 \; N)</math> сравнений, но если ее анализировать в рамках модели без явного задания параметров кэша, она производит <math>O(\frac{N}{B} \; log_2 \; \frac{N}{M})</math> переносов блоков памяти, что в <math>\Theta(log \; \frac{M} {B})</math> раз отличается от значения нижней границы (предполагается рекурсивная реализация бинарной сортировки слиянием, чтобы значение M входило в знаменатель компонента log N/M границы количества переносов блоков). Еще одним алгоритмом сортировки на базе сравнения является классический алгоритм быстрой сортировки (Quicksort), предложенный Хоаром в 1962 году [9], который выполняет ожидаемые <math>O(N \; log_2 \; N)</math> сравнений и ожидаемые <math>O(\frac{N}{B} \; log_2 \; \frac{N}{M})</math> переносов блоков памяти. Оба этих алгоритма обеспечивают достаточно высокую производительность в смысле количества переносов блоков благодаря тому, что они основаны на повторяющемся сканировании массивов – не использующий подобный подход алгоритм сортировки кучей (Heapsort) [10] демонстрирует весьма слабую эффективность в виде | ''Бинарная сортировка слиянием (Mergesort)'' выполняет <math>O(N \; log_2 \; N)</math> сравнений, но если ее анализировать в рамках модели без явного задания параметров кэша, она производит <math>O(\frac{N}{B} \; log_2 \; \frac{N}{M})</math> переносов блоков памяти, что в <math>\Theta(log \; \frac{M}{B})</math> раз отличается от значения нижней границы (предполагается рекурсивная реализация бинарной сортировки слиянием, чтобы значение M входило в знаменатель компонента log N/M границы количества переносов блоков). Еще одним алгоритмом сортировки на базе сравнения является классический алгоритм быстрой сортировки (Quicksort), предложенный Хоаром в 1962 году [9], который выполняет ожидаемые <math>O(N \; log_2 \; N)</math> сравнений и ожидаемые <math>O(\frac{N}{B} \; log_2 \; \frac{N}{M})</math> переносов блоков памяти. Оба этих алгоритма обеспечивают достаточно высокую производительность в смысле количества переносов блоков благодаря тому, что они основаны на повторяющемся сканировании массивов – не использующий подобный подход ''алгоритм сортировки кучей (Heapsort)'' [10] демонстрирует весьма слабую эффективность в виде <math>\Theta (N \; log_2 \; \frac{N}{M})</math> переносов блоков памяти. В модели ввода-вывода оптимальная эффективность <math>O(\frac{N}{B} \; log_{\frac{M}{B}} \; \frac{N}{M})</math> достигается в результате обобщения бинарной сортировки слиянием до <math>\Theta (\frac{M}{B})</math>-сторонней сортировки слиянием [1]. | ||
Фриго и др [8] представили два алгоритма сортировки без явного задания параметров кэша, которые также могут использоваться для перестановки массива элементов. Первый алгоритм [8, глава 4] носит название сортировки воронкой (Funnelsort) и напоминает классическую бинарную сортировку слиянием; второй алгоритм [8, глава 5] является алгоритмом сортировки распределением. Оба алгоритма обеспечивают оптимальные O( | Фриго и др [8] представили два алгоритма сортировки без явного задания параметров кэша, которые также могут использоваться для перестановки массива элементов. Первый алгоритм [8, глава 4] носит название ''сортировки воронкой (Funnelsort)'' и напоминает классическую бинарную сортировку слиянием; второй алгоритм [8, глава 5] является алгоритмом ''сортировки распределением''. Оба алгоритма обеспечивают ''оптимальные'' <math>O(\frac{N}{B} \; log_{\frac{M}{B}} \; \frac{N}{M})</math> переносов блоков памяти при условии соблюдения ''предположения о высоте кэша'' <math>M = \Omega (B^2) \;</math>. | ||
[[Файл:Sort_01.png]] | |||
Рис. 1. Общая рекурсия сортировки воронкой (слева) и 16-слияния (справа) | |||
'''Сортировка воронкой''' | '''Сортировка воронкой''' | ||
| Строка 28: | Строка 34: | ||
Базовая идея алгоритма сортировки воронкой заключается в перегруппировке процесса сортировки, выполняемого алгоритмом бинарной сортировки слиянием, таким образом, чтобы обработанные данные хранились «локально». Это достигается за счет применения двух базовых принципов: | Базовая идея алгоритма сортировки воронкой заключается в перегруппировке процесса сортировки, выполняемого алгоритмом бинарной сортировки слиянием, таким образом, чтобы обработанные данные хранились «локально». Это достигается за счет применения двух базовых принципов: | ||
(1) Рекурсия верхнего уровня, которая разбивает входной массив на | (1) Рекурсия верхнего уровня, которая разбивает входной массив на <math>N^{1/3} \;</math> последовательностей размера <math>N^{2/3} \;</math>, рекурсивно выполняет сортировку воронкой этих последовательностей и затем сливает полученные подпоследовательности при помощи алгоритма <math>N^{1/3} \;</math>-слияния. | ||
(2) Алгоритм k-слияния определяется рекурсивным образом. Он выполняет бинарное слияние k входных последовательностей согласно продуманному графику с соответствующим рекурсивным расположением данных в памяти с использованием буферов для хранения приостановленных процессов слияния (см. рис. 1). Были выполнены два последовательных упрощения без ухудшения асимптотического количества переносов блоков памяти. В работе [3] было доказано, что бинарное слияние может выполняться «ленивым» образом, | (2) ''Алгоритм k-слияния'' определяется рекурсивным образом. Он выполняет бинарное слияние k входных последовательностей согласно продуманному графику с соответствующим рекурсивным расположением данных в памяти с использованием буферов для хранения приостановленных процессов слияния (см. рис. 1). Были выполнены два последовательных упрощения без ухудшения асимптотического количества переносов блоков памяти. В работе [3] было доказано, что бинарное слияние может выполняться «ленивым» образом, что упрощает планирование слияния. В работе [5] было замечено, что рекурсивное расположение элементов k-слияния не является обязательным. Достаточно того, чтобы элемент k-слияния хранился в последовательном массиве, т.е. буферы могут располагаться в произвольном порядке, что упрощает алгоритм сборки для k-слияния. | ||
'''Неявная сортировка без явного задания параметров кэша''' | '''Неявная сортировка без явного задания параметров кэша''' | ||
Франческини в [7] показал, как неявно выполнить оптимальную сортировку без задания параметров кэша, используя только O(1) памяти – т.е. все данные хранятся во входном массиве,за исключением O(1) дополнительных слов с информацией. В частности, выходной массив является простой перестановкой входного. | Франческини в [7] показал, как неявно выполнить оптимальную сортировку без задания параметров кэша, используя только O(1) памяти – т.е. все данные хранятся во входном массиве, за исключением O(1) дополнительных слов с информацией. В частности, выходной массив является простой перестановкой входного. | ||
| Строка 46: | Строка 49: | ||
Теорема 1 ([4], следствие 3). Пусть | '''Теорема 1 ([4], следствие 3). Пусть <math>B_1 = 1 \;</math> и <math>B_2 = \frac{M}{2} \;</math>. Для любого алгоритма сортировки на базе сравнения, выполняющегося без явного задания параметров кэша, примем за <math>t_1 \;</math> и <math>t_2 \;</math> верхние границы количества операций ввода-вывода, произведенных над блоками размеров <math>B_1 \;</math> и <math>B_2 \;</math>. Если для вещественного числа <math>d \ge 0 \;</math> выполняется условие <math>t_2 = d \cdot \frac{N}{B^2} \; log_{ \frac{M}{B^2} } \; \frac{N}{B^2}</math>, то <math>t_1 > \frac{1}{8} \cdot N \; log_2 \; \frac{N}{M}</math>.''' | ||
Теорема доказывает, что сортировка на базе сравнения, выполняемая без явного задания параметров кэша и без предположения о высоте кэша, не может сравниться по эффективности с | Теорема доказывает, что сортировка на базе сравнения, выполняемая без явного задания параметров кэша и без предположения о высоте кэша, не может сравниться по эффективности с алгоритмами на базе модели ввода-вывода, в которой значения M и В известны алгоритму. Кроме того, из нее естественным образом следует, что если алгоритм без явного задания параметров кэша должен быть оптимальным по вводу-выводу для случая <math>B = \frac{M}{2} \;</math>, то наилучшим вариантом будет бинарная сортировка слияния: любой другой алгоритм будет также на <math>\Theta (log \; M)</math> отличаться от оптимальной границы количества переносов блоков для случая <math>M \gg B \;</math>. | ||
Для родственной задачи перестановки массива следующая теорема утверждает, что для всех возможных предположений о высоте кэша B < | Для родственной задачи перестановки массива следующая теорема утверждает, что для всех возможных предположений о высоте кэша <math>B \le M^{ \delta} \;</math> не существует алгоритма перестановки без явного задания параметров кэша с границей количества переносов блоков (даже для среднего случая), соответствующей нижней границе для наихудшего случая в модели ввода-вывода. | ||
Теорема 2 ([4], теорема 2). Для всех | '''Теорема 2 ([4], теорема 2). Для всех <math>\delta > 0 \;</math> не существует алгоритма перестановки без явного задания параметров кэша, который для всех <math>M \ge 2B \;</math> и <math>1 \le B \le M^{ \delta} \;</math> демонстрирует <math>O(min \{ N, \frac{N}{B} \; log_{\frac{M}{B}} \; \frac{N}{B} \} )</math> операций ввода-вывода, усредненных по всем возможным перестановкам размера N.''' | ||
== Применение == | == Применение == | ||
К сортировке без явного задания параметров кэша могут сведены многие задачи. В частности, Ардж и др. [2] разработали очередь с приоритетами без явного задания параметров кэша, основанную на сведении к сортировке. Кроме того, они показали, как применить | К сортировке без явного задания параметров кэша могут сведены многие задачи. В частности, Ардж и др. [2] разработали очередь с приоритетами без явного задания параметров кэша, основанную на сведении к сортировке. Кроме того, они показали, как применить очередь с приоритетами без явного задания параметров кэша для решения совокупности графовых задач, включая ранжирование списков, базисное возможное решение (BFS), DFS и минимальные остовные деревья. | ||
Бродаль и Фагерберг [3] показали, как модифицировать ленивый алгоритм сортировки воронкой без явного задания параметров кэша для решения некоторых задач вычислительной геометрии, включая пересечение ортогональных проекций отрезков прямых, нахождение всех ближайших соседей, | Бродаль и Фагерберг [3] показали, как модифицировать ленивый алгоритм сортировки воронкой без явного задания параметров кэша для решения некоторых задач вычислительной геометрии, включая пересечение ортогональных проекций отрезков прямых, нахождение всех ближайших соседей, задачу 3D maxima и пакетные ортогональные запросы диапазона. Все эти задачи могут быть решены при помощи вычислительного процесса, очень похожего на бинарную сортировку слиянием с дополнительными настройками в зависимости от задачи. Данная общая схема решения задач вычислительной геометрии носит название ''распределенного сметания''. | ||
== Открытые вопросы == | == Открытые вопросы == | ||
| Строка 67: | Строка 70: | ||
== Экспериментальные результаты == | == Экспериментальные результаты == | ||
Детальное экспериментальное исследование алгоритма сортировки воронкой Funnelsort без явного задания параметров кэша было выполнено в [5]. Основной результат исследования в [5] заключается в том, что грамотно реализованный алгоритм сортировки без явного задания параметров кэша может работать быстрее, чем настроенная реализация алгоритма быстрой сортировки Quicksort, для размеров входных данных, существенно превышающих объем оперативной памяти. Эта реализация также является не менее быстрой, чем недавняя реализация с явным заданием параметров кэша, включенная в тестирование. На дисковой памяти разница с алгоритмами быстрой сортировки и алгоритмами с явным заданием параметров кэша еще заметнее, хотя рассматриваемый алгоритм работает медленнее алгоритмов многосторонней сортировки слиянием, | Детальное экспериментальное исследование алгоритма сортировки воронкой Funnelsort без явного задания параметров кэша было выполнено в [5]. Основной результат исследования в [5] заключается в том, что грамотно реализованный алгоритм сортировки без явного задания параметров кэша может работать быстрее, чем настроенная реализация алгоритма быстрой сортировки Quicksort, для размеров входных данных, существенно превышающих объем оперативной памяти. Эта реализация также является не менее быстрой, чем недавняя реализация с явным заданием параметров кэша, включенная в тестирование. На дисковой памяти разница с алгоритмами быстрой сортировки и алгоритмами с явным заданием параметров кэша еще заметнее, хотя рассматриваемый алгоритм работает медленнее алгоритмов многосторонней сортировки слиянием Mergesort, оптимизированных для внешней памяти – таких как TPIE [6]. | ||
== Ссылка на код == | == Ссылка на код == | ||
| Строка 98: | Строка 101: | ||
10. Williams, J.W.J.: Algorithm 232: Heapsort. Commun. ACM 7(6), 347-348(1964) | 10. Williams, J.W.J.: Algorithm 232: Heapsort. Commun. ACM 7(6), 347-348(1964) | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 03:56, 7 декабря 2024
Ключевые слова и синонимы
Сортировка воронкой
Постановка задачи
Задача сортировки множества элементов является одной из наиболее активно изучавшихся вычислительных проблем. Первое исследование алгоритма сортировки без явного задания параметров кэша было представлено в 1999 году в основополагающей работе Фриго и др. [8], в которой была предложена структура без явного задания параметров кэша для разработки алгоритмов, предназначенных для компьютеров с неизвестными параметрами иерархической памяти.
Модель
В контексте подхода без явного задания параметров кэша вычислительная модель представляет машину с двумя уровнями памяти: кэш ограниченного объема и дополнительная память бесконечного объема. Предполагается, что объем кэша составляет M элементов, а перенос данных между двумя уровнями памяти осуществляется блоками по B последовательных элементов. Вычисления могут выполняться только над элементами, хранящимися в кэше; элементы из дополнительной памяти должны быть перемещены в кэш, прежде чем вычислительный процесс сможет получить к ним доступ. Программы пишутся так, словно они работают с единой памятью неограниченного объема, т.е. являются стандартными RAM-программами. Необходимые переносы содержимого между кэшем и дополнительной памятью выполняются моделью автоматически при помощи оптимальной автономной стратегии замещения кэша. Базовое предположение модели без явного задания параметров кэша заключается в том, что значения M и B неизвестны алгоритму, тогда как в предложенной Аггарвалом и Виттером [1] модели ввода-вывода алгоритм знает эти значения и явно выполняет перенос блоков памяти. Обстоятельное обсуждение модели без явного задания параметров кэша и ее отношения к многоуровневым иерархиям памяти приведено в [8].
Сортировка
Входным значением задачи сортировки является массив из N элементов, хранящийся во вспомогательной памяти, а выходное значение должно представлять собой массив во вспомогательной памяти, содержащий те же элементы в отсортированном порядке.
Основные результаты
В модели ввода-вывода были доказаны точные верхняя и нижняя границы для задачи сортировки и для задачи перестановки массива [1]. В частности, было доказано, что сортировка требует переноса [math]\displaystyle{ \Theta(\frac{N}{B} \; log_{\frac{M}{B}} \; \frac{N}{M}) }[/math] блоков памяти, а перестановка массива – [math]\displaystyle{ \Theta(min \{ N, \frac{N}{B} \; log_{\frac{M}{B}} \; \frac{N}{M} \}) }[/math] блоков. Поскольку нижние границы для модели ввода-вывода соблюдаются также и в модели без явного задания параметров кэша, нижние границы из работы [1] непосредственно задают нижнюю границу в [math]\displaystyle{ \Omega (\frac{N}{B} \; log_{\frac{M}{B}} \; \frac{N}{M}) }[/math] переносов содержимого памяти для сортировки без явного задания параметров кэша и [math]\displaystyle{ \Omega (min \{ N, \frac{N}{B} \; log_{\frac{M}{B}} \; \frac{N}{M} \} ) }[/math] переносов – для перестановки массива без явного задания параметров кэша. Верхняя граница из [1] не может быть применена к модели без явного задания параметров кэша, поскольку эти алгоритмы используют значения параметров B и M.
Бинарная сортировка слиянием (Mergesort) выполняет [math]\displaystyle{ O(N \; log_2 \; N) }[/math] сравнений, но если ее анализировать в рамках модели без явного задания параметров кэша, она производит [math]\displaystyle{ O(\frac{N}{B} \; log_2 \; \frac{N}{M}) }[/math] переносов блоков памяти, что в [math]\displaystyle{ \Theta(log \; \frac{M}{B}) }[/math] раз отличается от значения нижней границы (предполагается рекурсивная реализация бинарной сортировки слиянием, чтобы значение M входило в знаменатель компонента log N/M границы количества переносов блоков). Еще одним алгоритмом сортировки на базе сравнения является классический алгоритм быстрой сортировки (Quicksort), предложенный Хоаром в 1962 году [9], который выполняет ожидаемые [math]\displaystyle{ O(N \; log_2 \; N) }[/math] сравнений и ожидаемые [math]\displaystyle{ O(\frac{N}{B} \; log_2 \; \frac{N}{M}) }[/math] переносов блоков памяти. Оба этих алгоритма обеспечивают достаточно высокую производительность в смысле количества переносов блоков благодаря тому, что они основаны на повторяющемся сканировании массивов – не использующий подобный подход алгоритм сортировки кучей (Heapsort) [10] демонстрирует весьма слабую эффективность в виде [math]\displaystyle{ \Theta (N \; log_2 \; \frac{N}{M}) }[/math] переносов блоков памяти. В модели ввода-вывода оптимальная эффективность [math]\displaystyle{ O(\frac{N}{B} \; log_{\frac{M}{B}} \; \frac{N}{M}) }[/math] достигается в результате обобщения бинарной сортировки слиянием до [math]\displaystyle{ \Theta (\frac{M}{B}) }[/math]-сторонней сортировки слиянием [1].
Фриго и др [8] представили два алгоритма сортировки без явного задания параметров кэша, которые также могут использоваться для перестановки массива элементов. Первый алгоритм [8, глава 4] носит название сортировки воронкой (Funnelsort) и напоминает классическую бинарную сортировку слиянием; второй алгоритм [8, глава 5] является алгоритмом сортировки распределением. Оба алгоритма обеспечивают оптимальные [math]\displaystyle{ O(\frac{N}{B} \; log_{\frac{M}{B}} \; \frac{N}{M}) }[/math] переносов блоков памяти при условии соблюдения предположения о высоте кэша [math]\displaystyle{ M = \Omega (B^2) \; }[/math].
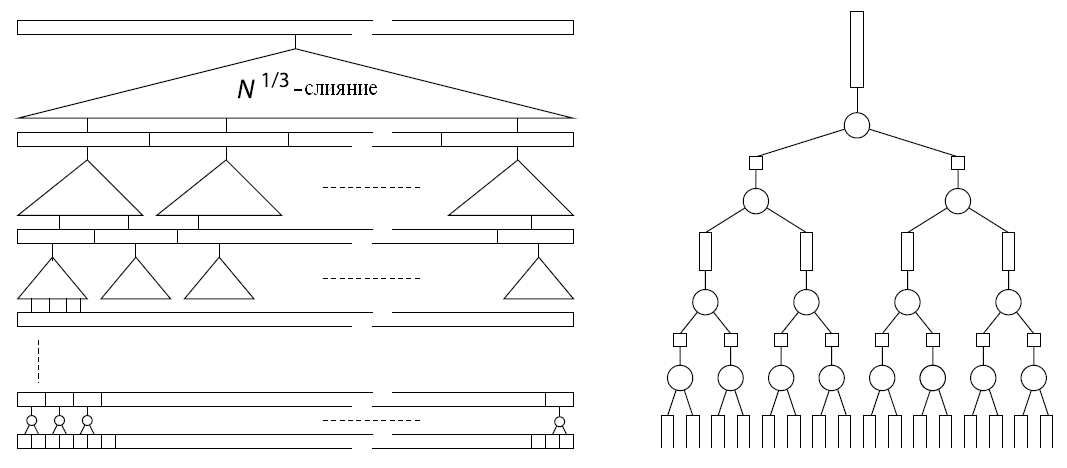
Рис. 1. Общая рекурсия сортировки воронкой (слева) и 16-слияния (справа)
Сортировка воронкой
Базовая идея алгоритма сортировки воронкой заключается в перегруппировке процесса сортировки, выполняемого алгоритмом бинарной сортировки слиянием, таким образом, чтобы обработанные данные хранились «локально». Это достигается за счет применения двух базовых принципов:
(1) Рекурсия верхнего уровня, которая разбивает входной массив на [math]\displaystyle{ N^{1/3} \; }[/math] последовательностей размера [math]\displaystyle{ N^{2/3} \; }[/math], рекурсивно выполняет сортировку воронкой этих последовательностей и затем сливает полученные подпоследовательности при помощи алгоритма [math]\displaystyle{ N^{1/3} \; }[/math]-слияния.
(2) Алгоритм k-слияния определяется рекурсивным образом. Он выполняет бинарное слияние k входных последовательностей согласно продуманному графику с соответствующим рекурсивным расположением данных в памяти с использованием буферов для хранения приостановленных процессов слияния (см. рис. 1). Были выполнены два последовательных упрощения без ухудшения асимптотического количества переносов блоков памяти. В работе [3] было доказано, что бинарное слияние может выполняться «ленивым» образом, что упрощает планирование слияния. В работе [5] было замечено, что рекурсивное расположение элементов k-слияния не является обязательным. Достаточно того, чтобы элемент k-слияния хранился в последовательном массиве, т.е. буферы могут располагаться в произвольном порядке, что упрощает алгоритм сборки для k-слияния.
Неявная сортировка без явного задания параметров кэша
Франческини в [7] показал, как неявно выполнить оптимальную сортировку без задания параметров кэша, используя только O(1) памяти – т.е. все данные хранятся во входном массиве, за исключением O(1) дополнительных слов с информацией. В частности, выходной массив является простой перестановкой входного.
Роль предположения о высоте кэша
Роль предположения о высоте кэша в контексте сортировки без явного задания параметров кэша изучали Бродаль и Фагерберг [4]. Дл случая, когда такого предположения не делается, они доказали следующую теорему:
Теорема 1 ([4], следствие 3). Пусть [math]\displaystyle{ B_1 = 1 \; }[/math] и [math]\displaystyle{ B_2 = \frac{M}{2} \; }[/math]. Для любого алгоритма сортировки на базе сравнения, выполняющегося без явного задания параметров кэша, примем за [math]\displaystyle{ t_1 \; }[/math] и [math]\displaystyle{ t_2 \; }[/math] верхние границы количества операций ввода-вывода, произведенных над блоками размеров [math]\displaystyle{ B_1 \; }[/math] и [math]\displaystyle{ B_2 \; }[/math]. Если для вещественного числа [math]\displaystyle{ d \ge 0 \; }[/math] выполняется условие [math]\displaystyle{ t_2 = d \cdot \frac{N}{B^2} \; log_{ \frac{M}{B^2} } \; \frac{N}{B^2} }[/math], то [math]\displaystyle{ t_1 \gt \frac{1}{8} \cdot N \; log_2 \; \frac{N}{M} }[/math].
Теорема доказывает, что сортировка на базе сравнения, выполняемая без явного задания параметров кэша и без предположения о высоте кэша, не может сравниться по эффективности с алгоритмами на базе модели ввода-вывода, в которой значения M и В известны алгоритму. Кроме того, из нее естественным образом следует, что если алгоритм без явного задания параметров кэша должен быть оптимальным по вводу-выводу для случая [math]\displaystyle{ B = \frac{M}{2} \; }[/math], то наилучшим вариантом будет бинарная сортировка слияния: любой другой алгоритм будет также на [math]\displaystyle{ \Theta (log \; M) }[/math] отличаться от оптимальной границы количества переносов блоков для случая [math]\displaystyle{ M \gg B \; }[/math].
Для родственной задачи перестановки массива следующая теорема утверждает, что для всех возможных предположений о высоте кэша [math]\displaystyle{ B \le M^{ \delta} \; }[/math] не существует алгоритма перестановки без явного задания параметров кэша с границей количества переносов блоков (даже для среднего случая), соответствующей нижней границе для наихудшего случая в модели ввода-вывода.
Теорема 2 ([4], теорема 2). Для всех [math]\displaystyle{ \delta \gt 0 \; }[/math] не существует алгоритма перестановки без явного задания параметров кэша, который для всех [math]\displaystyle{ M \ge 2B \; }[/math] и [math]\displaystyle{ 1 \le B \le M^{ \delta} \; }[/math] демонстрирует [math]\displaystyle{ O(min \{ N, \frac{N}{B} \; log_{\frac{M}{B}} \; \frac{N}{B} \} ) }[/math] операций ввода-вывода, усредненных по всем возможным перестановкам размера N.
Применение
К сортировке без явного задания параметров кэша могут сведены многие задачи. В частности, Ардж и др. [2] разработали очередь с приоритетами без явного задания параметров кэша, основанную на сведении к сортировке. Кроме того, они показали, как применить очередь с приоритетами без явного задания параметров кэша для решения совокупности графовых задач, включая ранжирование списков, базисное возможное решение (BFS), DFS и минимальные остовные деревья.
Бродаль и Фагерберг [3] показали, как модифицировать ленивый алгоритм сортировки воронкой без явного задания параметров кэша для решения некоторых задач вычислительной геометрии, включая пересечение ортогональных проекций отрезков прямых, нахождение всех ближайших соседей, задачу 3D maxima и пакетные ортогональные запросы диапазона. Все эти задачи могут быть решены при помощи вычислительного процесса, очень похожего на бинарную сортировку слиянием с дополнительными настройками в зависимости от задачи. Данная общая схема решения задач вычислительной геометрии носит название распределенного сметания.
Открытые вопросы
После выхода основополагающей статьи Фриго и др. [8], в которой была предложена структура без явного задания параметров кэша, было разработано множество алгоритмов с высокой теоретической эффективностью, однако внедрению этих алгоритмов было посвящено намного меньше работ. Важным направлением будущих работ будет получение новых экспериментальных результатов, упрочивающих положение модели без явного задания параметров кэша как эффективного средства работы с иерархической памятью.
Экспериментальные результаты
Детальное экспериментальное исследование алгоритма сортировки воронкой Funnelsort без явного задания параметров кэша было выполнено в [5]. Основной результат исследования в [5] заключается в том, что грамотно реализованный алгоритм сортировки без явного задания параметров кэша может работать быстрее, чем настроенная реализация алгоритма быстрой сортировки Quicksort, для размеров входных данных, существенно превышающих объем оперативной памяти. Эта реализация также является не менее быстрой, чем недавняя реализация с явным заданием параметров кэша, включенная в тестирование. На дисковой памяти разница с алгоритмами быстрой сортировки и алгоритмами с явным заданием параметров кэша еще заметнее, хотя рассматриваемый алгоритм работает медленнее алгоритмов многосторонней сортировки слиянием Mergesort, оптимизированных для внешней памяти – таких как TPIE [6].
Ссылка на код
http://kristoffer.vinther.name/projects/funnelsort/
См. также
Литература
1. Aggarwal, A., Vitter, J.S.: The input/output complexity of sorting and related problems. Commun. ACM 31(9), 1116-1127 (1988)
2. Arge, L., Bender, M.A., Demaine, E.D., Holland-Minkley, B., Munro, J.I.: Cache-oblivious priority queue and graph algorithm applications. In: Proc. 34th Annual ACM Symposium on Theory of Computing, pp. 268-276. ACM Press, New York (2002)
3. Brodal, G.S., Fagerberg, R.: Cache oblivious distribution sweeping. In: Proc. 29th International Colloquium on Automata, Languages, and Programming. Lecture Notes in Computer Science, vol. 2380, pp. 426-438. Springer, Berlin (2002)
4. Brodal, G.S., Fagerberg, R.: On the limits of cache-obliviousness. In: Proc. 35th Annual ACM Symposium on Theory of Computing, pp. 307-315. ACM Press, New York (2003)
5. Brodal, G.S., Fagerberg, R., Vinther, K.: Engineering a cache-oblivious sorting algorithm. ACM J. Exp. Algoritmics (Special Issue of ALENEX 2004) 12(2.2), 23 (2007)
6. Department of Computer Science, Duke University. TPIE: a transparent parallel I/O environment. http://www.cs.duke.edu/TPIE/. Accessed 2002
7. Franceschini, G.: Proximity mergesort: Optimal in-place sorting in the cache-oblivious model. In: Proceedings of the 15th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), SIAM, p. 291. Philadelphia, 2004
8. Frigo, M., Leiserson, C.E., Prokop, H., Ramachandran, S.: Cache- oblivious algorithms. In: Proc. 40th Annual Symposium on Foundations of Computer Science, pp. 285-297. IEEE Computer Society Press, Los Alamitos (1999)
9. Hoare, C.A.R.: Quicksort. Comput. J. 5(1), 10-15 (1962)
10. Williams, J.W.J.: Algorithm 232: Heapsort. Commun. ACM 7(6), 347-348(1964)