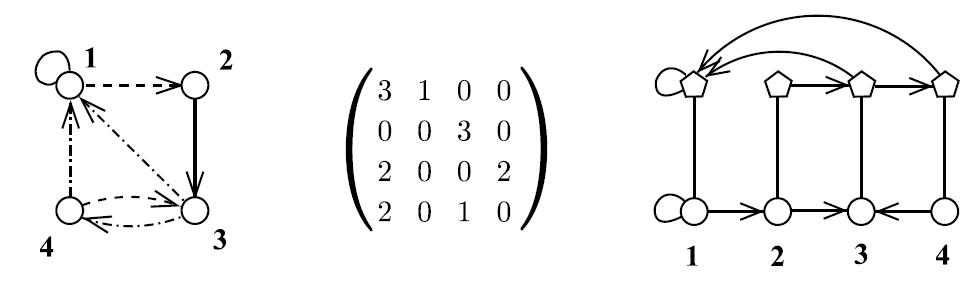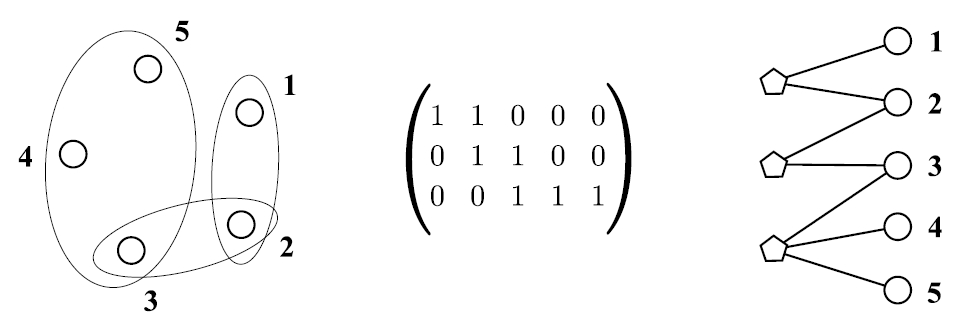Задача изоморфизма графов: различия между версиями
Irina (обсуждение | вклад) м (→Другие примеры) |
KVN (обсуждение | вклад) |
||
| (не показано 6 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
== Ключевые слова и синонимы == | == Ключевые слова и синонимы == | ||
'''Задача изоморфизма графов''' --- ''Graph isomorphism problem'' | |||
Паросочетания в графах (''Graph matching''); Группы симметрии (''Symmetry group'') | |||
== Постановка задачи == | == Постановка задачи == | ||
| Строка 29: | Строка 31: | ||
== Основные результаты == | == Основные результаты == | ||
Задача определения изоморфизма графов играет ключевую роль в современной теории сложности вычислений. Неизвестно, является ли она разрешимой за полиномиальное время, NP-полной или принадлежащей к классу co-NP. Подробнее об этом в работах [3] и [8]. Алгоритмы с полиномиальным временем | Задача определения изоморфизма графов играет ключевую роль в современной теории сложности вычислений. Неизвестно, является ли она разрешимой за полиномиальное время, NP-полной или принадлежащей к классу co-NP. Подробнее об этом в работах [3] и [8]. Алгоритмы с полиномиальным временем выполнения известны для многих специальных классов графов – в частности, графов ограниченного рода, графов с ограниченной степенью, ограниченной древесной шириной и ограниченной кратностью собственного значения. Самый быстрый теоретический алгоритм для графов общего вида требует <math>exp(n^{1/2+o(1)}) \; </math> времени [1], однако нет сведений о его практичности. | ||
В данном контексте наиболее практически полезным вариантом считается программа nauty. Брендан Маккей написал первую версию nauty в 1976 году, изложив метод ее работы в статье [5]. Известно [7], что она имеет экспоненциальное время | В данном контексте наиболее практически полезным вариантом считается программа nauty. Брендан Маккей написал первую версию nauty в 1976 году, изложив метод ее работы в статье [5]. Известно [7], что она имеет экспоненциальное время выполнения в наихудшем случае, но на практике этот наихудший случай встречается редко. | ||
| Строка 80: | Строка 82: | ||
Программа nauty позволяет выбирать между разреженными и плотными структурами данных и предлагает специальные варианты для некоторых конкретных сложных классов графов. В следующих примерах лучшие результаты были получены на единичном процессоре Intel Core-duo с тактовой частотой 2,4 ГГц. | Программа nauty позволяет выбирать между разреженными и плотными структурами данных и предлагает специальные варианты для некоторых конкретных сложных классов графов. В следующих примерах лучшие результаты были получены на единичном процессоре Intel Core-duo с тактовой частотой 2,4 ГГц. | ||
1. Граф произвольного вида с 10 000 вершин, p = | 1. Граф произвольного вида с 10 000 вершин, p = 1/2: 0,014 с. только для групп, 0,4 с. – с учетом канонической разметки. | ||
2. Произвольный кубический граф с 100 000 вершин: 8 с. | 2. Произвольный кубический граф с 100 000 вершин: 8 с. | ||
3. 1-мерный остов 20- | 3. 1-мерный остов 20-мерного куба (1 048 576 вершин, размер группы <math>2,5 \times 10^{24}</math>): 92 с. | ||
4. 3-мерная сетка размера 50 (125 000 вершин): 0,7 с. | 4. 3-мерная сетка размера 50 (125 000 вершин): 0,7 с. | ||
| Строка 91: | Строка 93: | ||
Примеры более сложных графов можно найти в документации программы nauty. | Примеры более сложных графов можно найти в документации программы nauty. | ||
== Ссылка на код == | == Ссылка на код == | ||
Исходный код nauty доступен по адресу http://cs.anu. edu.au/~bdm/nauty/. Еще одна реализация фрагмента nauty, посвященного группам автоморфизмов и оптимизированного для больших разреженных графов, доступна под названием saucy [ ]. Nauty входит в состав множества пакетов общего назначения, включая GAP, Magma и MuPad. | Исходный код nauty доступен по адресу http://cs.anu.edu.au/~bdm/nauty/. Еще одна реализация фрагмента nauty, посвященного группам автоморфизмов и оптимизированного для больших разреженных графов, доступна под названием saucy [2]. Nauty входит в состав множества пакетов общего назначения, включая GAP, Magma и MuPad. | ||
== См. также == | == См. также == | ||
| Строка 118: | Строка 118: | ||
8. Toran, J.: On the hardness of graph isomorphism. SIAM J. Comput. 33,1093-1108 (2004) | 8. Toran, J.: On the hardness of graph isomorphism. SIAM J. Comput. 33,1093-1108 (2004) | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 13:15, 25 ноября 2024
Ключевые слова и синонимы
Задача изоморфизма графов --- Graph isomorphism problem
Паросочетания в графах (Graph matching); Группы симметрии (Symmetry group)
Постановка задачи
Задача определения изоморфизма двух комбинаторных структур исключительно широко распространена и имеет приложения в самых разных областях. В задаче нахождения изоморфизма двух графов искомый изоморфизм представляет собой биекцию множеств вершин графов, порождающую биекцию множеств ребер графов. В случае, если второй граф является копией первого, изоморфизм является отображением графа на самого себя. Такой изоморфизм называется автоморфизмом или, менее формально, симметрией. Множество всех автоморфизмов образует группу относительно операции композиции, называемую группой автоморфизмов. Задача вычисления группы автоморфизмов весьма схожа с задачей определения изоморфизмов.
Изоморфизм графов тесно связан с другими типами изоморфизмов комбинаторных структур. Несколько примеров будут приведены в разделе «Применение».
Формальное описание
Граф представляет собой пару G = (V, E) конечных множеств, где E – множество пар (v, w) элементов V. Элементы множества V называются вершинами (или узлами), элементы множества E – ориентированными ребрами (или дугами). Контрарная пара (v, w); (w, v) ориентированных ребер ([math]\displaystyle{ v \ne w \; }[/math]) называется неориентированным ребром и обозначается {v, w}. Ориентированное ребро вида (v, v) также считается неориентированным и называется циклом (или петлей). Далее под «ребрами» будут пониматься неориентированные ребра, ориентированные ребра или оба типа ребер.
Пусть даны два графа [math]\displaystyle{ G_1 = (V_1, E_1) \; }[/math] и [math]\displaystyle{ G_2 = (V_2, E_2) \; }[/math]. Изоморфизм графа [math]\displaystyle{ G_1 \; }[/math] на [math]\displaystyle{ G_2 \; }[/math] представляет собой биекцию [math]\displaystyle{ V_1 \; }[/math] на [math]\displaystyle{ V_2 \; }[/math], такую, что она порождает биекцию [math]\displaystyle{ E_1 \; }[/math] на [math]\displaystyle{ E_2 \; }[/math]. Если [math]\displaystyle{ G_1 = G_2 \; }[/math], то изоморфизм является автоморфизмом [math]\displaystyle{ G_1 \; }[/math]. Множество всех автоморфизмов [math]\displaystyle{ G_1 \; }[/math] образует группу относительно операции композиции, называемую группой автоморфизмов [math]\displaystyle{ G_1 \; }[/math] и обозначаемую [math]\displaystyle{ Aut(G_1) \; }[/math].
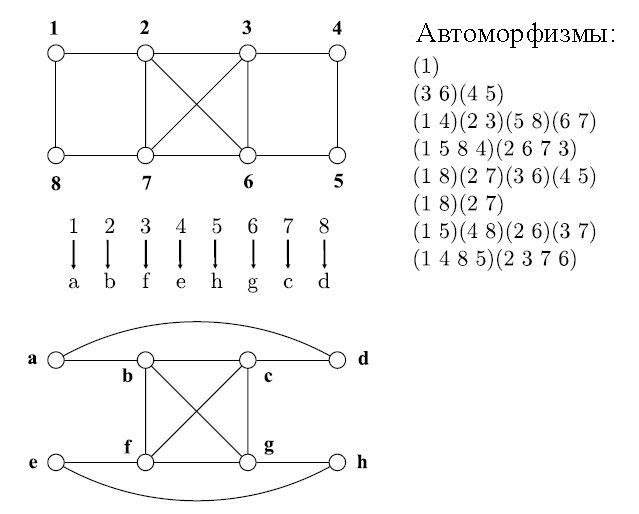
На рис. 1 представлены два изоморфных графа, а также изоморфизм между ними и группа автоморфизмов первого графа.
Рис. 1. Пример изоморфизма и группы изоморфизмов
Каноническая разметка
Практические варианты применения алгоритма проверки на изоморфизм графов не обязательно включают отдельные пары графов. Гораздо чаще требуется определить изоморфность данного графа любому представителю некоего набора графов (задача поиска в базе данных) либо найти классы изоморфизмов в имеющемся наборе графов (задача сортировки графов). Такие приложения не под силу алгоритмам, способным тестировать только пары графов.
Альтернативу представляет алгоритм канонической разметки. Его идея заключается в следующем: в каждом классе изоморфизмов имеется уникальный канонический граф, который может быть найден алгоритмом, получившим на входе любой граф класса изоморфизмов. Каноническим графом может быть, например, наименьший граф в классе изоморфизмов согласно какому-либо упорядочению (к примеру, лексикографическому). Практические алгоритмы обычно вычисляют каноническую форму с прицелом на эффективность, а не простоту описания.
Основные результаты
Задача определения изоморфизма графов играет ключевую роль в современной теории сложности вычислений. Неизвестно, является ли она разрешимой за полиномиальное время, NP-полной или принадлежащей к классу co-NP. Подробнее об этом в работах [3] и [8]. Алгоритмы с полиномиальным временем выполнения известны для многих специальных классов графов – в частности, графов ограниченного рода, графов с ограниченной степенью, ограниченной древесной шириной и ограниченной кратностью собственного значения. Самый быстрый теоретический алгоритм для графов общего вида требует [math]\displaystyle{ exp(n^{1/2+o(1)}) \; }[/math] времени [1], однако нет сведений о его практичности.
В данном контексте наиболее практически полезным вариантом считается программа nauty. Брендан Маккей написал первую версию nauty в 1976 году, изложив метод ее работы в статье [5]. Известно [7], что она имеет экспоненциальное время выполнения в наихудшем случае, но на практике этот наихудший случай встречается редко.
Программа nauty получает на вход граф с раскрашенными вершинами и выдает два результата; первый – это множество образующих для группы автоморфизмов, сохраняющих раскраску. Хотя в этом редко бывает необходимость, полная группа также может быть вычислена поэлементно. Вторым, необязательным результатом является канонический граф. Он имеет следующее свойство: два входных графа с одним и тем же числом вершин каждого цвета имеют один и тот же канонический граф в том и только том случае, если они являются изоморфными согласно изоморфизму с сохранением раскраски.
Поддерживаются две структуры данных для графов: упакованная матрица смежности, подходящая для небольших плотных графов, и список указателей, подходящий для больших разреженных графов.
Применение
Как было отмечено выше, программа nauty может обрабатывать графы с раскрашенными вершинами. Здесь описывается, как некоторые другие задачи нахождения изоморфизма графов могут быть решены при помощи отображения их на задачу о графах с раскрашенными вершинами.
Изоморфизм графов с раскрашенными ребрами
Изоморфизм двух графов – имеющих как раскрашенные вершины, так и раскрашенные ребра – определяется очевидным образом. Пример такого графа приведен на рис. 2.
Цвета определяются целыми числами 1, 2, 3 в матрице в центре рисунка. В правой части представлен эквивалентный граф с раскрашенными вершинами. В данном случае имеются два уровня, у каждого из которых собственная расцветка. Ребра цвета 1 представлены в виде ребра на первом (нижнем) уровне, ребра цвета 2 представлены в виде ребра на втором уровне, а ребра цвета 3 – в виде ребер на обоих уровнях. Теперь легко заметить, что группа автоморфизмов нового графа (а именно – ее действие на первом уровне) представляет собой группу автоморфизмов исходного графа. Кроме того, порядок, в котором канонический алгоритм разметки нового графа помечает вершины первого уровня, можно взять в качестве канонической разметки исходного графа.
В общем случае, если цвета ребер обозначены целыми числами [math]\displaystyle{ \{ 1; 2,... , 2^d - 1 \} \; }[/math], имеются d уровней, и двоичное разложение каждого числа, обозначающего цвет, определяет, какие уровни содержат ребра. Вертикальные потоки (каждый из которых соответствует одной вершине исходного графа) могут связываться посредством путей либо клик. Если исходный граф имел n вершин и k цветов, новый граф будет иметь [math]\displaystyle{ O(n \; log \; k) }[/math] вершин. Это значение может быть улучшено до [math]\displaystyle{ O(n \sqrt {log k} ) \; }[/math] вершин в случае использования негоризонтальных ребер.
Рис. 2. Изоморфизм графов с раскрашенными ребрами
Изоморфизм гиперграфов и схем
Гиперграф похож на неориентированный граф, за исключением того, что ребра могут представлять собой множества вершин любой величины, а не только величины 2. Подобная структура также называется схемой.
В левой части рисунка 3 представлен гиперграф с пятью вершинами, двумя ребрами величины 2 и одним ребром величины 3. Справа представлен эквивалентный ему граф с раскрашенными вершинами. Вершины слева, раскрашенные в один цвет, представляют ребра гиперграфа; вершины справа, раскрашенные в другой цвет, представляют дуги гиперграфа. Ребра графа обозначают отношение инцидентности (включения) гиперграфа.
Рис. 3. Изоморфизм гиперграфов/схем как изоморфизм графов
Матрица инцидентности ребер и вершин изображена в центральной части рисунка. Ею может быть любая бинарная матрица, позволяющая корректно отобразить тот факт, что рассматриваемая задача заключается в определении эквивалентности матриц (0, 1) при независимой перестановке строк и столбцов. Сочетая эту идею с предыдущей конструкцией, можно поддерживать подобное отношение эквивалентности на множестве матриц с произвольными значениями.
Другие примеры
Несколько примеров применения таких операций эквивалентности, как изотопия, имеющих важное значение для латинских квадратов и квазигрупп, можно найти в [6]. Еще один важный тип эквивалентности связывает матрицы посредством {-1,+1}. Помимо перестановки строк и столбцов, он позволяет умножать столбцы и строки на -1. Преобразование подобной задачи эквивалентности Адамара в задачу определения изоморфизма графов предложено в [4].
Экспериментальные результаты
Программа nauty позволяет выбирать между разреженными и плотными структурами данных и предлагает специальные варианты для некоторых конкретных сложных классов графов. В следующих примерах лучшие результаты были получены на единичном процессоре Intel Core-duo с тактовой частотой 2,4 ГГц.
1. Граф произвольного вида с 10 000 вершин, p = 1/2: 0,014 с. только для групп, 0,4 с. – с учетом канонической разметки.
2. Произвольный кубический граф с 100 000 вершин: 8 с.
3. 1-мерный остов 20-мерного куба (1 048 576 вершин, размер группы [math]\displaystyle{ 2,5 \times 10^{24} }[/math]): 92 с.
4. 3-мерная сетка размера 50 (125 000 вершин): 0,7 с.
5. 1027-вершинный сильно регулярный граф из произвольной системы троек Штейнера: 0,6 с.
Примеры более сложных графов можно найти в документации программы nauty.
Ссылка на код
Исходный код nauty доступен по адресу http://cs.anu.edu.au/~bdm/nauty/. Еще одна реализация фрагмента nauty, посвященного группам автоморфизмов и оптимизированного для больших разреженных графов, доступна под названием saucy [2]. Nauty входит в состав множества пакетов общего назначения, включая GAP, Magma и MuPad.
См. также
Литература
1. Babai, L., Luks, E.: Canonical labelling of graphs. In: Proceedings of the 15th Annual ACM Symposium on Theory of Computing, pp. 171-183.ACM,NewYork(1983)
2. Darga, P.T., Liffiton, M.H., Sakallah, K.A., Markov, I.L.: Exploiting Structure in Symmetry Generation for CNF. In: Proceedings of the 41st Design Automation Conference, 2004, pp. 530-534. Source code at http://vlsicad.eecs.umich.edu/BK/SAUCY/
3. Kobler, J., Schoning, U., Toran, J.: The Graph Isomorphism Problem: its structural complexity. Birkhauser, Boston (1993)
4. McKay, B.D.: Hadamard equivalence via graph isomorphism. Discret. Math. 27, 213-214 (1979)
5. McKay, B.D.: Practical graph isomorphism. Congr. Numer. 30, 45-87(1981)
6. McKay, B.D., Meynert, A., Myrvold, W.: Small Latin squares, quasi-groups and loops. J. Comb. Des. 15,98-119 (2007)
7. Miyazaki, T.: The complexity of McKay's canonical labelling algorithm. In: Groups and Computation, II. DIMACS Ser. Discret. Math.Theor. Comput. Sci., vol. 28, pp. 239-256. American Mathematical Society, Providence, RI (1997)
8. Toran, J.: On the hardness of graph isomorphism. SIAM J. Comput. 33,1093-1108 (2004)