Построение суффиксного дерева в иерархической памяти: различия между версиями
Irina (обсуждение | вклад) |
KVN (обсуждение | вклад) |
||
| (не показано 14 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
== Ключевые слова и синонимы == | == Ключевые слова и синонимы == | ||
Построение суффиксного массива; построение B-дерева на основе строки; построение полнотекстового индекса | |||
'''Построение суффиксного дерева в иерархической памяти''' --- ''Suffix Tree Construction in Hierarchical Memory'' | |||
Построение суффиксного массива (''Suffix array construction''); построение B-дерева на основе строки (''String B-tree construction''); построение полнотекстового индекса (''Fulltext index construction'') | |||
| Строка 7: | Строка 13: | ||
== Модель вычислений == | == Модель вычислений == | ||
Прежде чем рассуждать об алгоритмах и структурах данных на основе иерархической памяти, необходимо ввести модель вычислений, отражающую реальные ситуации, чтобы алгоритмы, успешно проявившие себя на модели, оказались бы столь же успешными на практике. Мы будем рассматривать модель с внешней памятью [ ], ставшей весьма популярной благодаря своей простоте и достаточной точности. Будем считать, что компьютер содержит два уровня памяти: внутреннюю память размера M и дисковую память неограниченного объема, действия над которой производятся в виде записи или чтения блоков данных размера B (называемых страницами дисковой памяти). Эффективность алгоритмов оценивается при помощи подсчета: (б) количества обращений к диску (операций ввода/вывода), (б) внутреннего времени выполнения (времени работы процессора), (в) количества страниц дисковой памяти, занятых структурой данных или использованных алгоритмом в качестве своего рабочего пространства. Это простая модель корректно предполагает, что хороший алгоритм для работы с внешней памятью должен использовать как пространственную, так и временную локальность. Разумеется, понятия «ввод/вывод» и «двухуровневое представление» распространяются на два любые уровня иерархи памяти при правильной установке параметров M и B. | Прежде чем рассуждать об алгоритмах и структурах данных на основе иерархической памяти, необходимо ввести модель вычислений, отражающую реальные ситуации, чтобы алгоритмы, успешно проявившие себя на модели, оказались бы столь же успешными на практике. Мы будем рассматривать модель с внешней памятью [16], ставшей весьма популярной благодаря своей простоте и достаточной точности. Будем считать, что компьютер содержит два уровня памяти: внутреннюю память размера M и дисковую память неограниченного объема, действия над которой производятся в виде записи или чтения блоков данных размера B (называемых страницами дисковой памяти). Эффективность алгоритмов оценивается при помощи подсчета: (б) количества обращений к диску (операций ввода/вывода), (б) внутреннего времени выполнения (времени работы процессора), (в) количества страниц дисковой памяти, занятых структурой данных или использованных алгоритмом в качестве своего рабочего пространства. Это простая модель корректно предполагает, что хороший алгоритм для работы с внешней памятью должен использовать как пространственную, так и временную локальность. Разумеется, понятия «ввод/вывод» и «двухуровневое представление» распространяются на два любые уровня иерархи памяти при правильной установке параметров M и B. | ||
== Нотация == | == Нотация == | ||
Пусть S[1, n] – строка, составленная из символов алфавита | Пусть S[1, n] – строка, составленная из символов алфавита <math>\Sigma \;</math>. Обозначим за <math>S_i \;</math> i-й [[суффикс]] строки S, за <math>lcp( \alpha, \beta) \;</math> – самый длинный общий префикс двух строк <math>\alpha \;</math> и <math>\beta \;</math>, а за lca(u, v) – [[наименьший общий предок|наименьшего общего предка]] двух вершин u и v в дереве. | ||
Суффиксное дерево S[1, n], которое далее будет обозначаться | Суффиксное дерево S[1, n], которое далее будет обозначаться <math>\mathcal{T}_S \;</math>, представляет собой дерево, хранящее все суффиксы S# в компактной форме, где <math>\# \notin \Sigma \;</math> – специальный символ (см. рис. 1). <math>\mathcal{T}_S \;</math> содержит n листьев с номерами от 1 до n, и любой путь из корня до листа читается как суффикс S#. Маркер конца # гарантирует, что ни один суффикс не является префиксом другого суффикса в S#. Каждая внутренняя вершина имеет по меньшей мере двух потомков; каждое ребро помечено непустой подстрокой из S. Никакие два ребра, выходящие из одной вершины, не могут начинаться с одной и той же буквы; вершины-братья лексикографически упорядочены в соответствии с этими буквами. Метки ребер закодированы парами целых чисел; например, S[x, y] представлено парой hx;yi. В результате все <math>\Theta(n^2) \;</math> подстрок S можно представить в O(n)-оптимальном пространстве при помощи структуры <math>\mathcal{T}_S \;</math> и кодирования ребер. Кроме того, обход листьев суффиксного дерева справа налево дает упорядоченное множество суффиксов S, также известное как [[суффиксный массив]] [12]. Заметим, что случай большого набора строк <math>\Delta = \{ S^1, S^2, ..., S^k \} \;</math> сводится к случаю одной длинной строки <math>S = S^1 \#_1 S^2 \#_2 ...S^k \#_k \;</math>, где <math>\#_i \notin \Sigma \;</math> – специальные символы. | ||
[[Файл:STC_HM.png]] | |||
Рисунок 1. Слева – суффиксное дерево S = ACACACCG, справа – компактное кодирование его ребер. Маркер конца # не представлен. Вершина v читается как строка ACAC. Каждая внутренняя вершина хранит длину связанной с ней строки, а каждый лист – начальную позицию соответствующего суффикса | |||
Разработано множество алгоритмов оптимального построения суффиксного дерева в RAM-модели (см. [1] и ссылки в этой работе). Однако большинство из них выявляет отсутствие локальности ссылок и в результате обнаруживает многие операции ввода/вывода, у которых размер индексированной строки слишком велик для того, чтобы поместиться во внутреннюю память компьютера. Это серьезная проблема, поскольку низкая скорость работы этих алгоритмов не позволяет использовать суффиксные деревья даже в приложениях среднего масштаба. Далее будут рассмотрены алгоритмические решения, эффективно выполняющие построение суффиксного дерева над большими наборами строк, производя при этом оптимальное количество операций ввода/вывода. Поскольку предполагается, что ребра, выходящие из вершины <math>\mathcal{T}_S \;</math>, лексикографически упорядочены, очевидной нижней границей при построении суффиксных деревьев является сортировка (можно рассматривать суффиксное дерево как перестановку). Для представленных алгоритмов сортировка является самым узким местом; таким образом, сложности алгоритма сортировки и алгоритма построения суффиксного дерева совпадают. | |||
Алгоритм «Разделяй и властвуй» | Алгоритм «Разделяй и властвуй» | ||
(1) Построить строку | (1) Построить строку <math>S'[j] = ранг \langle S[2j], S[2j + 1] \rangle \;</math>, и рекурсивно вычислить <math>\mathcal{T}_{S'} \;</math>. | ||
(2) Вывести из <math>\mathcal{T}_{S'} \;</math> уплотненное префиксное дерево (trie-дерево) <math>\mathcal{T}_o \;</math> со всеми суффиксами S, начинающимися с нечетных позиций. | |||
(3) Вывести из <math>\mathcal{T}_o \;</math> уплотненное префиксное дерево <math>\mathcal{T}_e \;</math> со всеми суффиксами S, начинающимися с четных позиций. | |||
(4) Слить <math>\mathcal{T}_o \;</math> и <math>\mathcal{T}_e \;</math> в целое суффиксное дерево <math>\mathcal{T}_S \;</math> следующим образом: | |||
(4.1) Наложить <math>\mathcal{T}_o \;</math> и <math>\mathcal{T}_e \;</math> на дерево <math>\mathcal{T}_M \;</math>. | |||
(4.2) Частично отделить <math>\mathcal{T}_M \;</math>, чтобы получить <math>\mathcal{T}_S \;</math>. | |||
Рисунок 2. Алгоритм прямого построения суффиксного дерева | |||
Алгоритм прямого построения суффиксного дерева | |||
== Основные результаты == | == Основные результаты == | ||
| Строка 49: | Строка 46: | ||
Первый алгоритм основан на подходе | Первый алгоритм основан на подходе «[[Разделяй и властвуй]]», позволяющем свести процесс построения к сортировке внешней памяти и нескольким низкоуровневым примитивам ввода/вывода. Он строит суффиксное дерево <math>\mathcal{T}_S \;</math> при помощи четырех макрошагов, представленных на рис. 2. Первые три шага несложно реализовать за <math>Sort(n) = O \Big( \frac{n}{B} \; log \; M/B \; \frac{n}{B} \Big) </math> операций ввода/вывода [16]. Последний шаг, слияние, является самым сложным, и именно объем операций ввода/вывода этого этапа определяет стоимость всего алгоритма. В работе [3] предложен элегантный способ слияния <math>\mathcal{T}_o \;</math> и <math>\mathcal{T}_e \;</math>: подшаг (4.1) временно ослабляет требование получения <math>\mathcal{T}_S \;</math> за один проход; он вслепую накладывает пути из <math>\mathcal{T}_o \;</math> и <math>\mathcal{T}_e \;</math>, сравнивая ребра только по их первым символам; затем подшаг (4.2) восстанавливает <math>\mathcal{T}_M \;</math>, определяя и отменяя чрезмерно наложенные пути эффективным с точки зрения количества операций ввода/вывода образом. Отметим, что сложность этого алгоритма, измеряемая по времени и по числу операций ввода/вывода, образует интересное рекурсивное соотношение: T(n) = T(n/2) + O(Sort(n)). | ||
Теорема 1 (Фарах-Колтон и др., 1999). Пусть дана произвольная строка S[1, n]; ее суффиксное дерево можно построить за O(Sort(n)) операций ввода/вывода и за время O( | '''Теорема 1 (Фарах-Колтон и др., 1999). Пусть дана произвольная строка S[1, n]; ее суффиксное дерево можно построить за O(Sort(n)) операций ввода/вывода и за время O(n log n), используя O(n/B) страниц дисковой памяти.''' | ||
Второй алгоритм кажется очень простым, элегантным и оптимальным по числу операций ввода/вывода; он успешно применяется для построения других индексированных структур данных – таких, как B-дерев на основе строки [5]. Основная идея заключается в выведении суффиксного дерева | Второй алгоритм кажется очень простым, элегантным и оптимальным по числу операций ввода/вывода; он успешно применяется для построения других индексированных структур данных – таких, как B-дерев на основе строки [5]. Основная идея заключается в выведении суффиксного дерева <math>\mathcal{T}_S \;</math> из суффиксного массива <math>\mathcal{A}_S \;</math> и массива lcp, который хранит длины самых длинных общих суффиксов для смежных суффиксов <math>\mathcal{A}_S \;</math>. Псевдокод алгоритма приведен на рис. 3. Заметим, что шаг (1) может задействовать любой алгоритм построения суффиксного массива с использованием внешней памяти. Здесь используется элегантный и оптимальный алгоритм перекоса Skew [9], требующий O(Sort(n)) операций ввода/вывода. Шаг 2 задействует в сумме O(n/B) операций ввода/вывода, используя стек, который хранит вершины текущего самого правого пути суффиксного дерева <math>\mathcal{T}_S \;</math> в обратном порядке, т.е. лист <math>\ell_i \;</math> находится наверху. Движение вверх, расщепление ребер или присоединение вершин в <math>\mathcal{T}_S \;</math> сводится к выталкиванию вершин из стека. В результате сложность этого алгоритма по времени и по числу операций ввода/вывода образует рекурсивное соотношение: T(n) = T(2n/3) + O(Sort(n)). | ||
Теорема 2 (Карккайнен и Сандерс, 2003). Пусть дана произвольная строка S[1, n]; ее суффиксное дерево можно построить за O(Sort(n)) операций ввода/вывода и за время O( | '''Теорема 2 (Карккайнен и Сандерс, 2003). Пусть дана произвольная строка S[1, n]; ее суффиксное дерево можно построить за O(Sort(n)) операций ввода/вывода и за время O(n log n), используя O(n/B) страниц дисковой памяти.''' | ||
(??? текст полностью совпадает) | (??? текст полностью совпадает с текстом теоремы 1) | ||
| Строка 68: | Строка 65: | ||
Алгоритм на базе суффиксного массива | Алгоритм на базе суффиксного массива | ||
(1) Построить суффиксный массив | (1) Построить суффиксный массив <math>\mathcal{A}_S \;</math> и массив <math>lcp_S \;</math> для строки S. | ||
(2) Задать начальное значение <math>\mathcal{T}_S \;</math> в виде единственного ребра, соединяющего корень с листом, ссылающимся на суффикс <math>\mathcal{A}_S \;</math> [1]. | |||
(2) For i = 2, ..., n: | |||
(2.1) Создать новый лист <math>\ell_i \;</math>, ссылающийся на суффикс <math>\mathcal{A}_S [i] \;</math>. | |||
(2.2) Двигаться вверх от <math>\ell_{i - 1} \;</math> до тех пор, пока не встретится вершина <math>u_i \;</math> с длиной строки <math>x_i \le lcp_S[i] \;</math>. | |||
(2.3) Если <math>x_i = lcp_S[i] \;</math>, присоединить лист <math>\ell_i \;</math> к <math>u_i \;</math>. | |||
(2.4) Если <math>x_i < lcp_S[i] \;</math>, создать вершину <math>u'_i \;</math> с длиной строки <math>x_i \;</math>, присоединить ее к <math>u_i \;</math>, а лист <math>\ell_i \;</math> – к <math>u'_i \;</math>. | |||
Рисунок 3. Алгоритм построения суффиксного дерева обходом суффиксного массива | |||
Алгоритм построения суффиксного дерева обходом суффиксного массива | |||
== Применение == | == Применение == | ||
| Строка 104: | Строка 92: | ||
В работе [8] авторы предложили инкрементный алгоритм под названием PrePar, который выполняет многократный проход по строке S и строит суффиксное дерево для поддиапазона суффиксов на каждом проходе. Для определенного пользователем параметра q поддиапазон суффиксов определяется как множество суффиксов, префиксом которых является одна и та же строка длины q. Поддиапазоны суффиксов порождают поддеревья | В работе [8] авторы предложили инкрементный алгоритм под названием PrePar, который выполняет многократный проход по строке S и строит суффиксное дерево для поддиапазона суффиксов на каждом проходе. Для определенного пользователем параметра q поддиапазон суффиксов определяется как множество суффиксов, префиксом которых является одна и та же строка длины q. Поддиапазоны суффиксов порождают поддеревья <math>\mathcal{T}_S \;</math>, которые, следовательно, могут быть построены независимо и извлечены из внутренней памяти по мере завершения. Эксперименты, упомянутые в работе [8], успешно индексировали 286 Мб/с при помощи 2 ГБ внутренней памяти. | ||
В работе [2] авторы предложили улучшенную версию алгоритма PrePar под названием DynaCluster, использующую динамическую технику для определения поддиапазонов суффиксов. В отличие от PrePar, DynaCluster не сканирует строку S вновь и вновь; он начинает работу с q-поддиапазонов и затем рекурсивно разбивает их подобно алгоритму DFS, если их размер превышает фиксированный порог т. Разбиение реализовано посредством просмотра следующих q знаков суффиксов поддиапазона. Эта кластеризация и облегченный DFS-просмотр дерева | |||
В работе [2] авторы предложили улучшенную версию алгоритма PrePar под названием DynaCluster, использующую динамическую технику для определения поддиапазонов суффиксов. В отличие от PrePar, DynaCluster не сканирует строку S вновь и вновь; он начинает работу с q-поддиапазонов и затем рекурсивно разбивает их подобно алгоритму DFS, если их размер превышает фиксированный порог т. Разбиение реализовано посредством просмотра следующих q знаков суффиксов поддиапазона. Эта кластеризация и облегченный DFS-просмотр дерева <math>\mathcal{T}_S \;</math> значительно снижают количество операций ввода/вывода, порождаемых частыми операциями расщепления ребер, которые появляются в процессе построения суффиксного дерева; а также позволяют эффективно обрабатывать перекошенные данные. В результате алгоритм DynaCluster строит суффиксные деревья со скоростью 200 мб/с с использованием всего лишь 16 МБ внутренней памяти. | |||
Недавно удалось улучшить параметры объема памяти и эффективность буферизации [15], что позволило построить суффиксное дерево на 3 Гб/с за 30 часов; в работе [1] было улучшено поведение RAM-алгоритмов с точки зрения операций ввода/вывода для построения суффиксного дерева в режиме онлайн, за счет разработки новой политики буферизации с низким уровнем издержек. | |||
== См. также == | == См. также == | ||
| Строка 148: | Строка 139: | ||
16. Vitter, J.: External memory algorithms and data structures: Dealing with MASSIVE DATA. ACM Comput. Surv. 33, 209-271 (2002) | 16. Vitter, J.: External memory algorithms and data structures: Dealing with MASSIVE DATA. ACM Comput. Surv. 33, 209-271 (2002) | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 08:13, 24 ноября 2024
Ключевые слова и синонимы
Построение суффиксного дерева в иерархической памяти --- Suffix Tree Construction in Hierarchical Memory
Построение суффиксного массива (Suffix array construction); построение B-дерева на основе строки (String B-tree construction); построение полнотекстового индекса (Fulltext index construction)
Постановка задачи
Суффиксное дерево – популярная структура данных для распознавания образцов в комбинаторике, поскольку ее элегантность позволяет использовать ее в множестве ситуаций – таких как поиск, сжатие и добыча данных, а также биоинформатика [6]. В таких приложениях огромные современные наборы данных используют многоуровневые структуры памяти, составляющие среду хранения данных современных компьютеров: кэши L1 и L2, внутренняя память, несколько жестких дисков и удаленных устройств, доступных по сети. Преимущество подобной организации памяти заключается в том, что она может обеспечить гарантированное время доступа к самым быстрым уровням (т.к. кэшу) и при этом сохранить низкую стоимость хранения данных в пересчете на одну ячейку памяти на самом дешевом уровне (диске), при условии, что данные должным образом кэшируются и предоставляются запрашивающим их алгоритмам. Проблемы игнорирования, касающиеся стоимости ссылок на память, могут даже привести к отказу от использования больших наборов входных данных. Инженеры-исследователи в настоящее время пытаются улучшить систему ввода/вывода, чтобы снизить влияние подобных проблем, однако хорошо известно [16], что улучшения, достижимые посредством должной организации данных и должным образом структурированных алгоритмических вычислений, заметно превышают самые значительные технологические достижения.
Модель вычислений
Прежде чем рассуждать об алгоритмах и структурах данных на основе иерархической памяти, необходимо ввести модель вычислений, отражающую реальные ситуации, чтобы алгоритмы, успешно проявившие себя на модели, оказались бы столь же успешными на практике. Мы будем рассматривать модель с внешней памятью [16], ставшей весьма популярной благодаря своей простоте и достаточной точности. Будем считать, что компьютер содержит два уровня памяти: внутреннюю память размера M и дисковую память неограниченного объема, действия над которой производятся в виде записи или чтения блоков данных размера B (называемых страницами дисковой памяти). Эффективность алгоритмов оценивается при помощи подсчета: (б) количества обращений к диску (операций ввода/вывода), (б) внутреннего времени выполнения (времени работы процессора), (в) количества страниц дисковой памяти, занятых структурой данных или использованных алгоритмом в качестве своего рабочего пространства. Это простая модель корректно предполагает, что хороший алгоритм для работы с внешней памятью должен использовать как пространственную, так и временную локальность. Разумеется, понятия «ввод/вывод» и «двухуровневое представление» распространяются на два любые уровня иерархи памяти при правильной установке параметров M и B.
Нотация
Пусть S[1, n] – строка, составленная из символов алфавита [math]\displaystyle{ \Sigma \; }[/math]. Обозначим за [math]\displaystyle{ S_i \; }[/math] i-й суффикс строки S, за [math]\displaystyle{ lcp( \alpha, \beta) \; }[/math] – самый длинный общий префикс двух строк [math]\displaystyle{ \alpha \; }[/math] и [math]\displaystyle{ \beta \; }[/math], а за lca(u, v) – наименьшего общего предка двух вершин u и v в дереве.
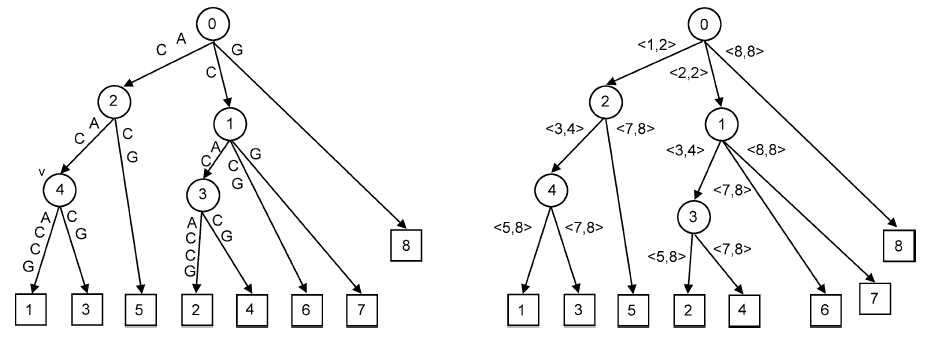
Суффиксное дерево S[1, n], которое далее будет обозначаться [math]\displaystyle{ \mathcal{T}_S \; }[/math], представляет собой дерево, хранящее все суффиксы S# в компактной форме, где [math]\displaystyle{ \# \notin \Sigma \; }[/math] – специальный символ (см. рис. 1). [math]\displaystyle{ \mathcal{T}_S \; }[/math] содержит n листьев с номерами от 1 до n, и любой путь из корня до листа читается как суффикс S#. Маркер конца # гарантирует, что ни один суффикс не является префиксом другого суффикса в S#. Каждая внутренняя вершина имеет по меньшей мере двух потомков; каждое ребро помечено непустой подстрокой из S. Никакие два ребра, выходящие из одной вершины, не могут начинаться с одной и той же буквы; вершины-братья лексикографически упорядочены в соответствии с этими буквами. Метки ребер закодированы парами целых чисел; например, S[x, y] представлено парой hx;yi. В результате все [math]\displaystyle{ \Theta(n^2) \; }[/math] подстрок S можно представить в O(n)-оптимальном пространстве при помощи структуры [math]\displaystyle{ \mathcal{T}_S \; }[/math] и кодирования ребер. Кроме того, обход листьев суффиксного дерева справа налево дает упорядоченное множество суффиксов S, также известное как суффиксный массив [12]. Заметим, что случай большого набора строк [math]\displaystyle{ \Delta = \{ S^1, S^2, ..., S^k \} \; }[/math] сводится к случаю одной длинной строки [math]\displaystyle{ S = S^1 \#_1 S^2 \#_2 ...S^k \#_k \; }[/math], где [math]\displaystyle{ \#_i \notin \Sigma \; }[/math] – специальные символы.
Рисунок 1. Слева – суффиксное дерево S = ACACACCG, справа – компактное кодирование его ребер. Маркер конца # не представлен. Вершина v читается как строка ACAC. Каждая внутренняя вершина хранит длину связанной с ней строки, а каждый лист – начальную позицию соответствующего суффикса
Разработано множество алгоритмов оптимального построения суффиксного дерева в RAM-модели (см. [1] и ссылки в этой работе). Однако большинство из них выявляет отсутствие локальности ссылок и в результате обнаруживает многие операции ввода/вывода, у которых размер индексированной строки слишком велик для того, чтобы поместиться во внутреннюю память компьютера. Это серьезная проблема, поскольку низкая скорость работы этих алгоритмов не позволяет использовать суффиксные деревья даже в приложениях среднего масштаба. Далее будут рассмотрены алгоритмические решения, эффективно выполняющие построение суффиксного дерева над большими наборами строк, производя при этом оптимальное количество операций ввода/вывода. Поскольку предполагается, что ребра, выходящие из вершины [math]\displaystyle{ \mathcal{T}_S \; }[/math], лексикографически упорядочены, очевидной нижней границей при построении суффиксных деревьев является сортировка (можно рассматривать суффиксное дерево как перестановку). Для представленных алгоритмов сортировка является самым узким местом; таким образом, сложности алгоритма сортировки и алгоритма построения суффиксного дерева совпадают.
Алгоритм «Разделяй и властвуй»
(1) Построить строку [math]\displaystyle{ S'[j] = ранг \langle S[2j], S[2j + 1] \rangle \; }[/math], и рекурсивно вычислить [math]\displaystyle{ \mathcal{T}_{S'} \; }[/math]. (2) Вывести из [math]\displaystyle{ \mathcal{T}_{S'} \; }[/math] уплотненное префиксное дерево (trie-дерево) [math]\displaystyle{ \mathcal{T}_o \; }[/math] со всеми суффиксами S, начинающимися с нечетных позиций. (3) Вывести из [math]\displaystyle{ \mathcal{T}_o \; }[/math] уплотненное префиксное дерево [math]\displaystyle{ \mathcal{T}_e \; }[/math] со всеми суффиксами S, начинающимися с четных позиций. (4) Слить [math]\displaystyle{ \mathcal{T}_o \; }[/math] и [math]\displaystyle{ \mathcal{T}_e \; }[/math] в целое суффиксное дерево [math]\displaystyle{ \mathcal{T}_S \; }[/math] следующим образом: (4.1) Наложить [math]\displaystyle{ \mathcal{T}_o \; }[/math] и [math]\displaystyle{ \mathcal{T}_e \; }[/math] на дерево [math]\displaystyle{ \mathcal{T}_M \; }[/math]. (4.2) Частично отделить [math]\displaystyle{ \mathcal{T}_M \; }[/math], чтобы получить [math]\displaystyle{ \mathcal{T}_S \; }[/math].
Рисунок 2. Алгоритм прямого построения суффиксного дерева
Основные результаты
Разработка эффективного алгоритма (относительно использования дисковой памяти) построения суффиксного дерева увенчалась успехом только в последние годы [4]. Мы представим два теоретических подхода, достигающих лучших (оптимальных!) границ по числу операций ввода/вывода в наихудшем случае, а следующей главе обсудим некоторые практические решения.
Первый алгоритм основан на подходе «Разделяй и властвуй», позволяющем свести процесс построения к сортировке внешней памяти и нескольким низкоуровневым примитивам ввода/вывода. Он строит суффиксное дерево [math]\displaystyle{ \mathcal{T}_S \; }[/math] при помощи четырех макрошагов, представленных на рис. 2. Первые три шага несложно реализовать за [math]\displaystyle{ Sort(n) = O \Big( \frac{n}{B} \; log \; M/B \; \frac{n}{B} \Big) }[/math] операций ввода/вывода [16]. Последний шаг, слияние, является самым сложным, и именно объем операций ввода/вывода этого этапа определяет стоимость всего алгоритма. В работе [3] предложен элегантный способ слияния [math]\displaystyle{ \mathcal{T}_o \; }[/math] и [math]\displaystyle{ \mathcal{T}_e \; }[/math]: подшаг (4.1) временно ослабляет требование получения [math]\displaystyle{ \mathcal{T}_S \; }[/math] за один проход; он вслепую накладывает пути из [math]\displaystyle{ \mathcal{T}_o \; }[/math] и [math]\displaystyle{ \mathcal{T}_e \; }[/math], сравнивая ребра только по их первым символам; затем подшаг (4.2) восстанавливает [math]\displaystyle{ \mathcal{T}_M \; }[/math], определяя и отменяя чрезмерно наложенные пути эффективным с точки зрения количества операций ввода/вывода образом. Отметим, что сложность этого алгоритма, измеряемая по времени и по числу операций ввода/вывода, образует интересное рекурсивное соотношение: T(n) = T(n/2) + O(Sort(n)).
Теорема 1 (Фарах-Колтон и др., 1999). Пусть дана произвольная строка S[1, n]; ее суффиксное дерево можно построить за O(Sort(n)) операций ввода/вывода и за время O(n log n), используя O(n/B) страниц дисковой памяти.
Второй алгоритм кажется очень простым, элегантным и оптимальным по числу операций ввода/вывода; он успешно применяется для построения других индексированных структур данных – таких, как B-дерев на основе строки [5]. Основная идея заключается в выведении суффиксного дерева [math]\displaystyle{ \mathcal{T}_S \; }[/math] из суффиксного массива [math]\displaystyle{ \mathcal{A}_S \; }[/math] и массива lcp, который хранит длины самых длинных общих суффиксов для смежных суффиксов [math]\displaystyle{ \mathcal{A}_S \; }[/math]. Псевдокод алгоритма приведен на рис. 3. Заметим, что шаг (1) может задействовать любой алгоритм построения суффиксного массива с использованием внешней памяти. Здесь используется элегантный и оптимальный алгоритм перекоса Skew [9], требующий O(Sort(n)) операций ввода/вывода. Шаг 2 задействует в сумме O(n/B) операций ввода/вывода, используя стек, который хранит вершины текущего самого правого пути суффиксного дерева [math]\displaystyle{ \mathcal{T}_S \; }[/math] в обратном порядке, т.е. лист [math]\displaystyle{ \ell_i \; }[/math] находится наверху. Движение вверх, расщепление ребер или присоединение вершин в [math]\displaystyle{ \mathcal{T}_S \; }[/math] сводится к выталкиванию вершин из стека. В результате сложность этого алгоритма по времени и по числу операций ввода/вывода образует рекурсивное соотношение: T(n) = T(2n/3) + O(Sort(n)).
Теорема 2 (Карккайнен и Сандерс, 2003). Пусть дана произвольная строка S[1, n]; ее суффиксное дерево можно построить за O(Sort(n)) операций ввода/вывода и за время O(n log n), используя O(n/B) страниц дисковой памяти.
(??? текст полностью совпадает с текстом теоремы 1)
Пока не очевидно, какой из этих алгоритмов окажется лучшим на практике. Первый из них использует рекурсию с параметром 1/2, но способствует значительному перерасходу памяти в силу управления топологией дерева; второй более эффективен в отношении использования памяти и проще для реализации, но использует рекурсию с параметром 2/3.
Алгоритм на базе суффиксного массива
(1) Построить суффиксный массив [math]\displaystyle{ \mathcal{A}_S \; }[/math] и массив [math]\displaystyle{ lcp_S \; }[/math] для строки S. (2) Задать начальное значение [math]\displaystyle{ \mathcal{T}_S \; }[/math] в виде единственного ребра, соединяющего корень с листом, ссылающимся на суффикс [math]\displaystyle{ \mathcal{A}_S \; }[/math] [1]. (2) For i = 2, ..., n: (2.1) Создать новый лист [math]\displaystyle{ \ell_i \; }[/math], ссылающийся на суффикс [math]\displaystyle{ \mathcal{A}_S [i] \; }[/math]. (2.2) Двигаться вверх от [math]\displaystyle{ \ell_{i - 1} \; }[/math] до тех пор, пока не встретится вершина [math]\displaystyle{ u_i \; }[/math] с длиной строки [math]\displaystyle{ x_i \le lcp_S[i] \; }[/math]. (2.3) Если [math]\displaystyle{ x_i = lcp_S[i] \; }[/math], присоединить лист [math]\displaystyle{ \ell_i \; }[/math] к [math]\displaystyle{ u_i \; }[/math]. (2.4) Если [math]\displaystyle{ x_i \lt lcp_S[i] \; }[/math], создать вершину [math]\displaystyle{ u'_i \; }[/math] с длиной строки [math]\displaystyle{ x_i \; }[/math], присоединить ее к [math]\displaystyle{ u_i \; }[/math], а лист [math]\displaystyle{ \ell_i \; }[/math] – к [math]\displaystyle{ u'_i \; }[/math].
Рисунок 3. Алгоритм построения суффиксного дерева обходом суффиксного массива
Применение
В работах [4] и [6] можно найти длинный список вариантов применения больших суффиксных деревьев.
Открытые вопросы
Недавние теоретические и практические достижения разрушили сложившееся убеждение «суффиксные деревья непрактичны, за исключением случаев, когда размер текста настолько мал, что суффиксное дерево помещается во внутренней памяти» [13]. Пусть имеется суффиксное дерево. Теперь известно (см., например, [4, 10]), как отобразить его не систему с дисковой памятью, чтобы обеспечить эффективный по числу операций ввода/вывода обход для последующего поиска по образцу. В силу этого задачи хранения и построения суффиксного дерева требуют дальнейшего изучения.
Пространственная оптимизация тесно связана с временной оптимизацией в системе с дисковой памятью, так что алгоритм построения сжатых суффиксных деревьев является ключом к масштабированию вплоть до гигабайт данных за разумное время. В этой области ведутся активные исследования и получены интересные результаты (см., например, [14]), которые еще не в полной мере реализованы в практических условиях.
Интересная теоретическая задача заключается в создании алгоритма построения суффиксного дерева, оптимального по числу операций ввода/вывода и по объему занимаемой памяти, пропорциональным энтропии индексированной строки. Чем выше степень сжимаемости строки, тем меньше должны быть требования алгоритма к памяти. Некоторые результаты уже получены [7, 10, 11], однако вопросы сжатия и числа операций ввода/вывода в объединенной форме пока не решены.
Экспериментальные результаты
Интерес к построению больших суффиксных деревьев в последние годы возрос в связи с новейшими открытиями в технологии секвенирования, позволившими быстро набрать базу данных по ДНК и белкам. В некоторых недавних работах [1, 2, 8, 15] были предложены новые практичные алгоритмы, позволяющие масштабировать задачи до гигабайт в час. Как ни удивительно, эти алгоритмы основаны на неэффективных по использованию дисковой памяти схемах, зато они правильно выбирают порядок вставки суффиксов и грамотно используют внутреннюю память в качестве буфера, так что их эффективность несущественно отличается от теоретического «бутылочного горлышка» ввода/вывода.
В работе [8] авторы предложили инкрементный алгоритм под названием PrePar, который выполняет многократный проход по строке S и строит суффиксное дерево для поддиапазона суффиксов на каждом проходе. Для определенного пользователем параметра q поддиапазон суффиксов определяется как множество суффиксов, префиксом которых является одна и та же строка длины q. Поддиапазоны суффиксов порождают поддеревья [math]\displaystyle{ \mathcal{T}_S \; }[/math], которые, следовательно, могут быть построены независимо и извлечены из внутренней памяти по мере завершения. Эксперименты, упомянутые в работе [8], успешно индексировали 286 Мб/с при помощи 2 ГБ внутренней памяти.
В работе [2] авторы предложили улучшенную версию алгоритма PrePar под названием DynaCluster, использующую динамическую технику для определения поддиапазонов суффиксов. В отличие от PrePar, DynaCluster не сканирует строку S вновь и вновь; он начинает работу с q-поддиапазонов и затем рекурсивно разбивает их подобно алгоритму DFS, если их размер превышает фиксированный порог т. Разбиение реализовано посредством просмотра следующих q знаков суффиксов поддиапазона. Эта кластеризация и облегченный DFS-просмотр дерева [math]\displaystyle{ \mathcal{T}_S \; }[/math] значительно снижают количество операций ввода/вывода, порождаемых частыми операциями расщепления ребер, которые появляются в процессе построения суффиксного дерева; а также позволяют эффективно обрабатывать перекошенные данные. В результате алгоритм DynaCluster строит суффиксные деревья со скоростью 200 мб/с с использованием всего лишь 16 МБ внутренней памяти.
Недавно удалось улучшить параметры объема памяти и эффективность буферизации [15], что позволило построить суффиксное дерево на 3 Гб/с за 30 часов; в работе [1] было улучшено поведение RAM-алгоритмов с точки зрения операций ввода/вывода для построения суффиксного дерева в режиме онлайн, за счет разработки новой политики буферизации с низким уровнем издержек.
См. также
- Сортировка без явного задания параметров кэша
- Сортировка строк
- Построение суффиксного массива
- Построение суффиксного дерева в равнодоступной адресной машине (RAM)
- Индексация текста
Литература
1. Bedathur, S.J., Haritsa, J.R.: Engineering a fast online persistent suffix tree construction., In: Proc. 20th International Conference on Data Engineering, pp. 720-731, Boston, USA (2004)
2. Cheung, C., Yu, J., Lu, H.: Constructing suffix tree for gigabyte sequences with megabyte memory. IEEE Trans. Knowl. Data Eng. 17,90-105 (2005)
3. Farach-Colton, M., Ferragina, P., Muthukrishnan, S.: On the sorting-complexity of suffix tree construction. J. ACM 47 987-1011 (2000)
4. Ferragina, P.: Handbook of Computational Molecular Biology. In: Computer and Information Science Series, ch. 35 on "String search in external memory: algorithms and data structures". Chapman & Hall/CRC, Florida (2005)
5. Ferragina, P., Grossi, R.: The string B-tree: A new data structure for string search in external memory and its applications. J. ACM 46, 236-280 (1999)
6. Gusfield, D.: Algorithms on Strings,Trees and Sequences: Computer Science and Computational Biology. Cambridge University Press, Cambridge (1997)
7. Hon, W., Sadakane, K., Sung, W.: Breaking a time-and-space barrier in constructing full-text indices. In: IEEE Symposium on Foundations of Computer Science (FOCS), 2003, pp. 251 -260
8. Hunt, E., Atkinson, M., Irving, R.: Database indexing for large DNA and protein sequence collections. Int. J. Very Large Data Bases 11, 256-271 (2002)
9. Karkkainen, J., Sanders, P., Burkhardt, S.: Linear work suffix array construction. J. ACM 53,918-936 (2006)
10. Ko, P., Aluru, S.: Optimal self-adjusting trees for dynamic string data in secondary storage. In: Symposium on String Processing and Information Retrieval (SPIRE). LNCS, vol.4726, pp. 184-194. Springer, Berlin (2007)
11. Makinen, V., Navarro, G.: Dynamic Entropy-Compressed Sequences and Full-Text Indexes. In: Proc. 17th Symposium on Combinatorial Pattern Matching (CPM). LNCS, vol. 4009, pp. 307-318. Springer, Berlin (2006)
12. Manber, U., Myers, G.: Suffix arrays: a new method for on-line string searches. SIAM J. Comput. 22,935-948 (1993)
13. Navarro, G., Baeza-Yates, R.: A hybrid indexing method for approximate string matching. J. Discret. Algorithms 1, 21-49 (2000)
14. Navarro, G., Makinen, V.: Compressed full text indexes. ACM Comput. Surv.39(1) (2007)
15. Tata, S., Hankins, R.A., Patel, J.M.: Practical suffix tree construction. In: Proc. 13th International Conference on Very Large Data Bases (VLDB), pp. 36^7, Toronto, Canada (2004)
16. Vitter, J.: External memory algorithms and data structures: Dealing with MASSIVE DATA. ACM Comput. Surv. 33, 209-271 (2002)