R-дерево: различия между версиями
Irina (обсуждение | вклад) |
KVN (обсуждение | вклад) |
||
| (не показано 8 промежуточных версий 1 участника) | |||
| Строка 13: | Строка 13: | ||
== R-деревья == | == R-деревья == | ||
R-дерево, введенное Гуттманом [9], представляет собой многовариантное дерево <math>\mathcal{T} \;</math>, очень похожее на [[B-дерево]], использующееся для хранения множества S, благодаря чему на оконные запросы можно эффективно получать ответы. Каждая вершина <math>\mathcal{T} \;</math> помещается в один блок диска. Гиперкубы из S хранятся только в листьях <math>\mathcal{T} \;</math>. Все листья <math>\mathcal{T} \;</math> находятся на одном и том же уровне, в каждом из них хранится | R-дерево, введенное Гуттманом [9], представляет собой многовариантное дерево <math>\mathcal{T} \;</math>, очень похожее на [[B-дерево (дерево многоканального поиска)|B-дерево]], использующееся для хранения множества S, благодаря чему на оконные запросы можно эффективно получать ответы. Каждая вершина <math>\mathcal{T} \;</math> помещается в один блок диска. Гиперкубы из S хранятся только в листьях <math>\mathcal{T} \;</math>. Все листья <math>\mathcal{T} \;</math> находятся на одном и том же уровне, в каждом из них хранится <math>\Theta(B) \;</math> гиперкубов из S; каждая внутренняя вершина, кроме корня, имеет <math>\Theta(B) \;</math> инцидентных ей исходящих дуг. Корень <math>\mathcal{T} \;</math> имеет только две исходящих дуги. Для любой вершины <math>u \in \mathcal{T} \;</math> обозначим за R(u) наименьший параллельный осям гиперкуб, называемый [[минимальный ограничивающий прямоугольник|минимальным ограничивающим прямоугольником]], который включает все гиперкубы, хранящиеся ниже u. В каждой внутренней вершине <math>v \in \mathcal{T} \;</math> с детьми <math>v_1, ..., v_b \;</math> ограничивающий прямоугольник <math>R(v_i) \;</math> хранится вместе с указателем на <math>v_i \;</math> для i = 1, ..., k. Заметим, что эти ограничивающие прямоугольники могут перекрываться. На рис. 1 представлен пример R-дерева в двух измерениях. | ||
| Строка 24: | Строка 24: | ||
Любое R-дерево занимает линейное число O(N/B) блоков на диске, однако у разных R-деревьев может быть разная стоимость запроса, обновления и построения. При анализе сложности оконных запросов наряду со значениями N, M и B также учитывается размер выходных данных | Любое R-дерево занимает линейное число O(N/B) блоков на диске, однако у разных R-деревьев может быть разная стоимость запроса, обновления и построения. При анализе сложности оконных запросов наряду со значениями N, M и B также учитывается размер выходных данных T. | ||
== Основные результаты == | == Основные результаты == | ||
Хотя структура R-дерева ограничена, группировка гиперкубов в листья и группировка поддеревьев в поддеревья большей величины допускает немалую долю свободы. Различные стратегии группировки приводят к созданию различных вариантов R-деревьев. Большинство существующих R-деревьев используют различные эвристики для группировки гиперкубов, «близких» друг к другу в пространственном отношении, так что оконному запросу не придется посещать слишком много «лишних» вершин. В общем случае имеются два способа построения R-дерева: повторная вставка и массовая загрузка. К первому типу алгоритмов относятся исходное R-дерево [9], R+-дерево [15], R*-дерево [6] и т.п. Эти алгоритмы используют O( | Хотя структура R-дерева ограничена, группировка гиперкубов в листья и группировка поддеревьев в поддеревья большей величины допускает немалую долю свободы. Различные стратегии группировки приводят к созданию различных вариантов R-деревьев. Большинство существующих R-деревьев используют различные эвристики для группировки гиперкубов, «близких» друг к другу в пространственном отношении, так что оконному запросу не придется посещать слишком много «лишних» вершин. В общем случае имеются два способа построения R-дерева: повторная вставка и массовая загрузка. К первому типу алгоритмов относятся исходное R-дерево [9], R+-дерево [15], R*-дерево [6] и т.п. Эти алгоритмы используют <math>O(log_B \; N)</math> операций ввода-вывода для вставки объекта и, следовательно, <math>O(N log \; B \; N)</math> операций ввода-вывода для построения R-дерева на множестве S, что плохо масштабируется для больших значений N. Если множество S известно заранее, намного эффективнее оказывается организовать массовую загрузку всего R-дерева за один проход. Существует множество алгоритмов массовой загрузки – с ними можно ознакомиться, например, в [7, 8, 10, 11, 13]. Большинство этих алгоритмов строит R-дерево за <math>O(N/B \; log_{M/B} \; N/B)</math> операций ввода-вывода (именно столько их требуется для сортировки N элементов); полученные в результате R-деревья обычно оказываются лучше созданных при помощи повторной вставки. За прошедшие десятилетия специалистами по работе с базами данных было опубликовано много работ, посвященных R-деревьям, полный список которых был бы слишком обширным. Манопулос и др. [14] приводят великолепный обзор литературы по данному вопросу. Однако ни один из вышеупомянутых вариантов R-деревьев не гарантирует нужной сложности выполнения запроса; Ардж и др. [3] построили пример, демонстрирующий, что в случае некоторых из наиболее популярных R-деревьев приходится посещать все вершины, не дав ни одного ответа. | ||
| Строка 33: | Строка 34: | ||
Теорема 1 ([1, 12]). Имеется множество из N точек в пространстве <math>\mathbb{R}_d \;</math>, такое, что для любого R-дерева <math>\mathcal{T} \;</math>, построенного на этих точках, существует пустой оконный запрос, для выполнения которого алгоритм запроса должен посетить | '''Теорема 1 ([1, 12]). Имеется множество из N точек в пространстве <math>\mathbb{R}_d \;</math>, такое, что для любого R-дерева <math>\mathcal{T} \;</math>, построенного на этих точках, существует пустой оконный запрос, для выполнения которого алгоритм запроса должен посетить <math>\Omega((N/B)^{1 - 1/d}) \;</math> вершин <math>\mathcal{T} \;</math>.''' | ||
| Строка 39: | Строка 40: | ||
Теорема 2 ([3]). Для любого множества S, содержащего N параллельных осям гиперкубов в пространстве <math>\mathbb{R}_d \;</math>, R-дерево с приоритетами отвечает на оконный запрос при помощи O{ | '''Теорема 2 ([3]). Для любого множества S, содержащего N параллельных осям гиперкубов в пространстве <math>\mathbb{R}_d \;</math>, R-дерево с приоритетами отвечает на оконный запрос при помощи <math>O((N/B)^{1 - 1/d} + T/B) \;</math> операций ввода-вывода и может быть построено при помощи <math>O(N/B \; log_{M/B} \; N/B)</math> операций ввода-вывода.''' | ||
Было также отмечено, что R-деревья с приоритетами на практике работают весьма успешно [3]. Однако неизвестно, как эффективно обновлять их с сохранением границы для наихудшего случая. Для поддержки операций вставки и удаления был предложен логарифмический метод [3], однако получающаяся структура уже не будет R-деревом. Заметим, однако, что нижняя граница из теоремы 1 относится только к R-деревьям. Если структура данных не ограничена определением R-дерева, в процессе выполнения оконных запросов можно получить более подходящие границы; см., например, [4]. | Было также отмечено, что R-деревья с приоритетами на практике работают весьма успешно [3]. Однако неизвестно, как эффективно обновлять их с сохранением границы для наихудшего случая. Для поддержки операций вставки и удаления был предложен логарифмический метод [3], однако получающаяся структура уже не будет R-деревом. Заметим, однако, что нижняя граница из теоремы 1 относится только к R-деревьям. Если структура данных не ограничена определением R-дерева, в процессе выполнения оконных запросов можно получить более подходящие границы; см., например, [4]. | ||
== Применение == | == Применение == | ||
R-деревья широко использовались на практике благодаря своей простоте, возможности хранения пространственных объектов различных форм и способности отвечать на различные запросы. Они применяются в таких областях, как географические информационные системы (ГИС), САПР, машинное зрение и робототехника. Если объекты не являются параллельными осям гиперкубами, их часто можно аппроксимировать минимальными ограничивающими прямоугольниками и затем построить R-дерево на основе этих прямоугольников. При поиске ответа на оконный запрос вначале R-дерево используется для локализации всех пересекающихся ограничивающих прямоугольников, после чего следует этап фильтрации с точной проверкой объектов. R-дерево также можно использовать для выполнения запросов других типов – например, объединенных запросов по шаблону, запросов о ближайших соседях и т.п. В объединенных запросах каждый объект o множества S ассоциирован с весом w(o) | R-деревья широко использовались на практике благодаря своей простоте, возможности хранения пространственных объектов различных форм и способности отвечать на различные запросы. Они применяются в таких областях, как географические информационные системы (ГИС), САПР, машинное зрение и робототехника. Если объекты не являются параллельными осям гиперкубами, их часто можно аппроксимировать минимальными ограничивающими прямоугольниками и затем построить R-дерево на основе этих прямоугольников. При поиске ответа на оконный запрос вначале R-дерево используется для локализации всех пересекающихся ограничивающих прямоугольников, после чего следует этап фильтрации с точной проверкой объектов. R-дерево также можно использовать для выполнения запросов других типов – например, объединенных запросов по шаблону, запросов о ближайших соседях и т.п. В объединенных запросах каждый объект o множества S ассоциирован с весом <math>w(o) \in \mathbb{R} \;</math>; задача состоит в вычислении <math>\sum w(o) \;</math>, где сумма берется по всем объектам, пересекающим диапазон вопроса Q. Алгоритм запроса точно тот же, что и раньше, за тем исключением, что он подсчитывает сумму при обходе R-дерева и может пропускать целое поддерево с корнем в вершине u, если R(u) полностью содержится в Q. Для нахождения ближайшего соседа точки запроса q поддерживается очередь приоритетов; в ней хранятся все вершины u, которые могут содержать объект, находящийся ближе к найденному до настоящего момента ближайшему соседу. Приоритетом u в очереди является расстояние между q и R(u). Поиск прекращается, когда текущий ближайший сосед оказывается ближе самого высокого элемента в очереди приоритетов. Однако пока неизвестны границы для наихудшего случая для ответа на подобные вопросы при помощи R-деревьев, хотя на практике они работают очень хорошо. | ||
== Открытые вопросы == | == Открытые вопросы == | ||
Несколько интересных вопросов, касающихся R-деревьев, остаются нерешенными. Среди них можно выделить следующие. | Несколько интересных вопросов, касающихся R-деревьев, остаются нерешенными. Среди них можно выделить следующие. | ||
• Возможно ли разработать R-дерево с оптимальной границей запросов O(( | • Возможно ли разработать R-дерево с оптимальной границей запросов <math>O((N/B)^{1 - 1/d} + T/B) \;</math> и возможностью эффективного обновления или доказать значение нижней границы стоимости обновления у такого R-дерева? | ||
• Существует ли R-дерево, поддерживающее объединенные запросы для параллельных осям гиперкубов за | • Существует ли R-дерево, поддерживающее объединенные запросы для параллельных осям гиперкубов за <math>O((N/B)^{1 - 1/d}) \;</math> операций ввода-вывода? Это было бы оптимально, поскольку нижняя граница из теоремы 1 также верна для объединенных запросов на R-деревьях. Впрочем, стоит отметить, что для запросов о ближайших соседях не существует сублинейной границы в наихудшем случае, поскольку несложно разработать пример для наихудшего случая, в котором расстояние между точкой запроса q и любым ограничивающим прямоугольником будет меньше расстояния между q и его истинным ближайшим соседом. | ||
• Когда оконный запрос Q стягивается в точку, иначе говоря, когда требуется найти все гиперкубы из S, содержащие точку запроса, такую задачу часто называют прокалывающим запросом или запросом с замыканием на точку. Нижняя граница из теоремы 1 для этого специального случая не действует; для модели сильной индексируемости в [5] была доказана нижняя граница | • Когда оконный запрос Q стягивается в точку, иначе говоря, когда требуется найти все гиперкубы из S, содержащие точку запроса, такую задачу часто называют ''прокалывающим запросом'' или ''запросом с замыканием на точку''. Нижняя граница из теоремы 1 для этого специального случая не действует; для модели сильной индексируемости в [5] была доказана нижняя граница <math>\Theta(log_2 \; N + T/B)</math>. Любопытно было бы узнать истинную сложность прокалывающих запросов при помощи R-деревьев, которая находится в интервале между <math>\Theta(log_2 \; N + T/B)</math> и <math>O((N/B)^{1 - 1/d} + T/B) \;</math>. | ||
| Строка 106: | Строка 107: | ||
15. Sellis, T., Roussopoulos, N., Faloutsos, C.: The R+-tree: A dynamic index for multi-dimensional objects. In: Proc. International Conference on Very Large Databases, 1987, pp. 507-518 | 15. Sellis, T., Roussopoulos, N., Faloutsos, C.: The R+-tree: A dynamic index for multi-dimensional objects. In: Proc. International Conference on Very Large Databases, 1987, pp. 507-518 | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 04:50, 22 ноября 2024
Ключевые слова и синонимы
Пространственные базы данных; структуры данных с внешней памятью
Постановка задачи
Формулировка задачи и модель ввода-вывода
Пусть S – множество из N гиперкубов, параллельных осям, в пространстве [math]\displaystyle{ \mathbb{R}_d \; }[/math]. Одной из простейших операций к пространственной базе данных является ответ на оконные запросы на множестве S. Оконный запрос Q также представляет собой параллельный осям гиперкуб в пространстве [math]\displaystyle{ \mathbb{R}_d \; }[/math], который предлагает вернуть все гиперкубы из S, имеющие пересечение с Q. Поскольку S, как правило, очень велико и пространственная база также имеет очень большой размер, задача состоит в разработке структуры данных с внешней памятью на дисках (в посвященной базам данных литературе такая структура часто называется индексом), позволяющей эффективно отвечать на подобные оконные запросы. Кроме того, при заданном множестве S структура данных должна быть эффективной в построении и поддерживать вставку и удаление объектов.
При рассмотрении структур данных с внешней памятью в качестве модели вычислений нередко используется стандартная модель внешней памяти [2], также называемая моделью ввода-вывода. В данной модели машина состоит из внешней памяти неограниченного объема (диска) и основной памяти размера M. Блок из В последовательных элементов может быть передан между основной и дисковой памятью за одну операцию ввода-вывода. Структура данных внешней памяти хранится на диске по блокам, но вычисление может производиться только над элементами в основной памяти, так что любая операция (такая как запрос, обновление и построение) на структуре данных должна включать некоторое число операций ввода-вывода; количеством операций ввода-вывода измеряется сложность основной операции.
R-деревья
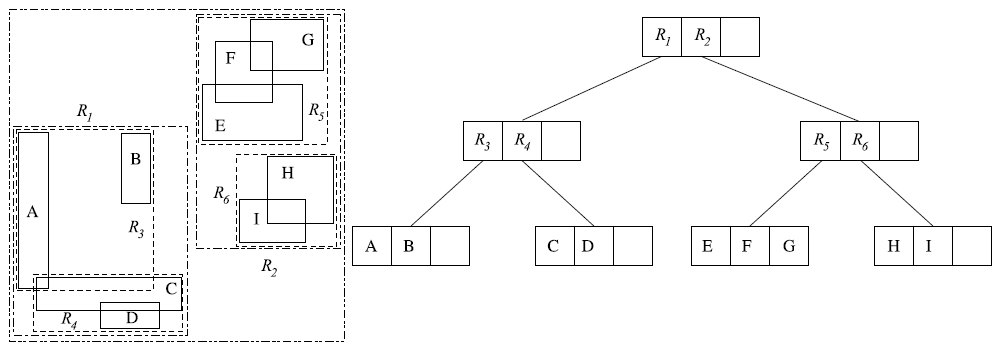
R-дерево, введенное Гуттманом [9], представляет собой многовариантное дерево [math]\displaystyle{ \mathcal{T} \; }[/math], очень похожее на B-дерево, использующееся для хранения множества S, благодаря чему на оконные запросы можно эффективно получать ответы. Каждая вершина [math]\displaystyle{ \mathcal{T} \; }[/math] помещается в один блок диска. Гиперкубы из S хранятся только в листьях [math]\displaystyle{ \mathcal{T} \; }[/math]. Все листья [math]\displaystyle{ \mathcal{T} \; }[/math] находятся на одном и том же уровне, в каждом из них хранится [math]\displaystyle{ \Theta(B) \; }[/math] гиперкубов из S; каждая внутренняя вершина, кроме корня, имеет [math]\displaystyle{ \Theta(B) \; }[/math] инцидентных ей исходящих дуг. Корень [math]\displaystyle{ \mathcal{T} \; }[/math] имеет только две исходящих дуги. Для любой вершины [math]\displaystyle{ u \in \mathcal{T} \; }[/math] обозначим за R(u) наименьший параллельный осям гиперкуб, называемый минимальным ограничивающим прямоугольником, который включает все гиперкубы, хранящиеся ниже u. В каждой внутренней вершине [math]\displaystyle{ v \in \mathcal{T} \; }[/math] с детьми [math]\displaystyle{ v_1, ..., v_b \; }[/math] ограничивающий прямоугольник [math]\displaystyle{ R(v_i) \; }[/math] хранится вместе с указателем на [math]\displaystyle{ v_i \; }[/math] для i = 1, ..., k. Заметим, что эти ограничивающие прямоугольники могут перекрываться. На рис. 1 представлен пример R-дерева в двух измерениях.
Рисунок 1. Пример R-дерева в двух измерениях
Пусть имеется оконный запрос Q. Процесс ответа на запрос начинает работу с корня дерева [math]\displaystyle{ \mathcal{T} \; }[/math] и посещает все вершины u, у которых R(u) пересекается с Q. Достигнув листа v, он проверяет каждый гиперкуб, хранящийся в v, решая, следует ли включить его в ответ. Корректность алгоритма очевидна, а его эффективность (количество операций ввода-вывода) определяется количеством посещенных вершин.
Любое R-дерево занимает линейное число O(N/B) блоков на диске, однако у разных R-деревьев может быть разная стоимость запроса, обновления и построения. При анализе сложности оконных запросов наряду со значениями N, M и B также учитывается размер выходных данных T.
Основные результаты
Хотя структура R-дерева ограничена, группировка гиперкубов в листья и группировка поддеревьев в поддеревья большей величины допускает немалую долю свободы. Различные стратегии группировки приводят к созданию различных вариантов R-деревьев. Большинство существующих R-деревьев используют различные эвристики для группировки гиперкубов, «близких» друг к другу в пространственном отношении, так что оконному запросу не придется посещать слишком много «лишних» вершин. В общем случае имеются два способа построения R-дерева: повторная вставка и массовая загрузка. К первому типу алгоритмов относятся исходное R-дерево [9], R+-дерево [15], R*-дерево [6] и т.п. Эти алгоритмы используют [math]\displaystyle{ O(log_B \; N) }[/math] операций ввода-вывода для вставки объекта и, следовательно, [math]\displaystyle{ O(N log \; B \; N) }[/math] операций ввода-вывода для построения R-дерева на множестве S, что плохо масштабируется для больших значений N. Если множество S известно заранее, намного эффективнее оказывается организовать массовую загрузку всего R-дерева за один проход. Существует множество алгоритмов массовой загрузки – с ними можно ознакомиться, например, в [7, 8, 10, 11, 13]. Большинство этих алгоритмов строит R-дерево за [math]\displaystyle{ O(N/B \; log_{M/B} \; N/B) }[/math] операций ввода-вывода (именно столько их требуется для сортировки N элементов); полученные в результате R-деревья обычно оказываются лучше созданных при помощи повторной вставки. За прошедшие десятилетия специалистами по работе с базами данных было опубликовано много работ, посвященных R-деревьям, полный список которых был бы слишком обширным. Манопулос и др. [14] приводят великолепный обзор литературы по данному вопросу. Однако ни один из вышеупомянутых вариантов R-деревьев не гарантирует нужной сложности выполнения запроса; Ардж и др. [3] построили пример, демонстрирующий, что в случае некоторых из наиболее популярных R-деревьев приходится посещать все вершины, не дав ни одного ответа.
С теоретической точки зрения можно сделать два основных вывода о сложности запросов к R-деревьям в наихудшем случае.
Теорема 1 ([1, 12]). Имеется множество из N точек в пространстве [math]\displaystyle{ \mathbb{R}_d \; }[/math], такое, что для любого R-дерева [math]\displaystyle{ \mathcal{T} \; }[/math], построенного на этих точках, существует пустой оконный запрос, для выполнения которого алгоритм запроса должен посетить [math]\displaystyle{ \Omega((N/B)^{1 - 1/d}) \; }[/math] вершин [math]\displaystyle{ \mathcal{T} \; }[/math].
R-дерево с приоритетами, предложенное Арджем и др. [3], соответствует вышеприведенной нижней границе.
Теорема 2 ([3]). Для любого множества S, содержащего N параллельных осям гиперкубов в пространстве [math]\displaystyle{ \mathbb{R}_d \; }[/math], R-дерево с приоритетами отвечает на оконный запрос при помощи [math]\displaystyle{ O((N/B)^{1 - 1/d} + T/B) \; }[/math] операций ввода-вывода и может быть построено при помощи [math]\displaystyle{ O(N/B \; log_{M/B} \; N/B) }[/math] операций ввода-вывода.
Было также отмечено, что R-деревья с приоритетами на практике работают весьма успешно [3]. Однако неизвестно, как эффективно обновлять их с сохранением границы для наихудшего случая. Для поддержки операций вставки и удаления был предложен логарифмический метод [3], однако получающаяся структура уже не будет R-деревом. Заметим, однако, что нижняя граница из теоремы 1 относится только к R-деревьям. Если структура данных не ограничена определением R-дерева, в процессе выполнения оконных запросов можно получить более подходящие границы; см., например, [4].
Применение
R-деревья широко использовались на практике благодаря своей простоте, возможности хранения пространственных объектов различных форм и способности отвечать на различные запросы. Они применяются в таких областях, как географические информационные системы (ГИС), САПР, машинное зрение и робототехника. Если объекты не являются параллельными осям гиперкубами, их часто можно аппроксимировать минимальными ограничивающими прямоугольниками и затем построить R-дерево на основе этих прямоугольников. При поиске ответа на оконный запрос вначале R-дерево используется для локализации всех пересекающихся ограничивающих прямоугольников, после чего следует этап фильтрации с точной проверкой объектов. R-дерево также можно использовать для выполнения запросов других типов – например, объединенных запросов по шаблону, запросов о ближайших соседях и т.п. В объединенных запросах каждый объект o множества S ассоциирован с весом [math]\displaystyle{ w(o) \in \mathbb{R} \; }[/math]; задача состоит в вычислении [math]\displaystyle{ \sum w(o) \; }[/math], где сумма берется по всем объектам, пересекающим диапазон вопроса Q. Алгоритм запроса точно тот же, что и раньше, за тем исключением, что он подсчитывает сумму при обходе R-дерева и может пропускать целое поддерево с корнем в вершине u, если R(u) полностью содержится в Q. Для нахождения ближайшего соседа точки запроса q поддерживается очередь приоритетов; в ней хранятся все вершины u, которые могут содержать объект, находящийся ближе к найденному до настоящего момента ближайшему соседу. Приоритетом u в очереди является расстояние между q и R(u). Поиск прекращается, когда текущий ближайший сосед оказывается ближе самого высокого элемента в очереди приоритетов. Однако пока неизвестны границы для наихудшего случая для ответа на подобные вопросы при помощи R-деревьев, хотя на практике они работают очень хорошо.
Открытые вопросы
Несколько интересных вопросов, касающихся R-деревьев, остаются нерешенными. Среди них можно выделить следующие.
• Возможно ли разработать R-дерево с оптимальной границей запросов [math]\displaystyle{ O((N/B)^{1 - 1/d} + T/B) \; }[/math] и возможностью эффективного обновления или доказать значение нижней границы стоимости обновления у такого R-дерева?
• Существует ли R-дерево, поддерживающее объединенные запросы для параллельных осям гиперкубов за [math]\displaystyle{ O((N/B)^{1 - 1/d}) \; }[/math] операций ввода-вывода? Это было бы оптимально, поскольку нижняя граница из теоремы 1 также верна для объединенных запросов на R-деревьях. Впрочем, стоит отметить, что для запросов о ближайших соседях не существует сублинейной границы в наихудшем случае, поскольку несложно разработать пример для наихудшего случая, в котором расстояние между точкой запроса q и любым ограничивающим прямоугольником будет меньше расстояния между q и его истинным ближайшим соседом.
• Когда оконный запрос Q стягивается в точку, иначе говоря, когда требуется найти все гиперкубы из S, содержащие точку запроса, такую задачу часто называют прокалывающим запросом или запросом с замыканием на точку. Нижняя граница из теоремы 1 для этого специального случая не действует; для модели сильной индексируемости в [5] была доказана нижняя граница [math]\displaystyle{ \Theta(log_2 \; N + T/B) }[/math]. Любопытно было бы узнать истинную сложность прокалывающих запросов при помощи R-деревьев, которая находится в интервале между [math]\displaystyle{ \Theta(log_2 \; N + T/B) }[/math] и [math]\displaystyle{ O((N/B)^{1 - 1/d} + T/B) \; }[/math].
Экспериментальные результаты
Почти все исследования на R-деревьях включают экспериментальные оценки, чаще всего в двух измерениях. В частности, R-дерево Гильберта [10, 11] продемонстрировало высокую эффективность разрешения запросов наряду с простотой построения. Алгоритм вставки для R*-деревьев [6] часто использовался для обновления R-деревьев. В книге Манопулоса и др. [14] можно ознакомиться с обширными дискуссиями о практической эффективности R-деревьев.
Наборы данных
Помимо некоторых синтетических наборов данных, данные системы TIGER/Line (http://www.census.gov/geo/www/tiger/) Бюро переписи населения США нередко использовались в качестве реальных данных для проверки R-деревьев. На портале R-деревьев (http://www.rtreeportal.org/) также можно найти немало интересных наборов данных.
Ссылка на код
Код для различных вариантов R-деревьев представлен на портале R-деревьев (http://www.rtreeportal.org/). Код для R-дерева с приоритетами доступен по адресу http://www.cse.ust.hk/~yike/prtree/.
См. также
Литература
1. Agarwal, P.K., de Berg, M., Gudmundsson, J., Hammar, M., Haverkort, H.J.: Box-trees and R-trees with near-optimal query time. Discret. Comput. Geom. 28, 291 -312 (2002)
2. Aggarwal, A., Vitter, J.S.: The input/output complexity of sorting and related problems. In: Communications of the ACM, vol. 31, pp. 1116-1127(1988)
3. Arge, L., de Berg, M., Haverkort, H.J., Yi, K.: The priority R-tree: A practically efficient and worst-case optimal R-tree. In: Proc. SIGMOD International Conference on Management of Data, 2004, pp. 347-358
4. Arge, L., Samoladas, V., Vitter, J.S.: On two-dimensional indexability and optimal range search indexing. In: Proc. ACM Symposium on Principles of Database Systems, 1999, pp. 346-357
5. Arge, L., Samoladas, V., Yi, K.: Optimal external memory planar point enclosure. In: Proc. European Symposium on Algorithms, 2004
6. Beckmann, N., Kriegel, H.-P., Schneider, R., Seeger, B.: The R*-tree: An efficient and robust access method for points and rectangles. In: Proc. SIGMOD International Conference on Management of Data, 1990, pp. 322-331
7. DeWitt, D.J., Kabra, N., Luo, J., Patel, J.M., Yu, J.-B.: Client-server paradise. In: Proc. International Conference on Very Large Databases, 1994, pp. 558-569
8. Garcfa, Y.J., Lopez, M.A., Leutenegger, S.T.: A greedy algorithm for bulk loading R-trees. In: Proc. 6th ACM Symposium on Advances in GIS, 1998, pp. 163-164
9. Guttman, A.: R-trees: A dynamic index structure for spatial searching. In: Proc. SIGMOD International Conference on Management of Data, 1984, pp. 47-57
10. Kamel, I., Faloutsos, C.: On packing R-trees. In: Proc. International Conference on Information and Knowledge Management, 1993, pp. 490-499
11. Kamel, I., Faloutsos, C.: Hilbert R-tree: An improved R-tree using fractals. In: Proc. International Conference on Very Large Databases, 1994, pp. 500-509
12. Kanth, K.V.R., Singh, A.K.: Optimal dynamic range searching in non-replicating index structures. In: Proc. International Conference on Database Theory. LNCS, vol. 1540, pp. 257-276 (1999)
13. Leutenegger, S.T., Lopez, M.A., Edington, J.: STR: A simple and efficient algorithm for R-tree packing. In: Proc. 13th IEEE International Conference on Data Engineering, 1997, pp. 497-506
14. Manolopoulos, Y., Nanopoulos, A., Papadopoulos, A.N., Theodoridis, Y.: R-trees: Theory and Applications. Springer, London (2005)
15. Sellis, T., Roussopoulos, N., Faloutsos, C.: The R+-tree: A dynamic index for multi-dimensional objects. In: Proc. International Conference on Very Large Databases, 1987, pp. 507-518