Параметризованные алгоритмы графического представления графов: различия между версиями
Irina (обсуждение | вклад) |
KVN (обсуждение | вклад) |
||
| (не показано 12 промежуточных версий 1 участника) | |||
| Строка 43: | Строка 43: | ||
== Основные результаты == | == Основные результаты == | ||
Для задач, для которых не предполагается существования полиномиальных алгоритмов, очень желательно найти точные алгоритмы с экспоненциальным временем | Для задач, для которых не предполагается существования полиномиальных алгоритмов, очень желательно найти точные алгоритмы с экспоненциальным временем выполнения. | ||
| Строка 62: | Строка 62: | ||
'''Теорема 4 ([9]). Если k – минимальное количество пересечений ребер в экземпляре задачи OSCM <math>(G = (V_1, | '''Теорема 4 ([9]). Если k – минимальное количество пересечений ребер в экземпляре задачи OSCM <math>(G = (V_1, V_2, E), <_1 )\;</math>, то <math>\sum_{u, v \in V_2, u \ne v} min \{ c_{uv}, v_{vu} \} \le k < 1,4664 \sum_{u, v \in V_2, u \ne v} min \{ c_{uv}, v_{vu} \} \;</math>'''. | ||
Нагамочи предложил алгоритм | Нагамочи предложил аппроксимационный алгоритм с коэффициентом меньше 1,4664. | ||
Далее, для | Далее, для любой вершины <math>u \in V_2 \;</math> с <math>deg(u) > 0 \;</math> обозначим за <math>l_u \;</math> самого левого соседа u в <math>L_1 \;</math>, а за <math>r_u \;</math> – самого правого. Две вершины <math>u, v \in V_2 \;</math> называются неподходящими, если существует некоторое <math>x \in N(u) \;</math>, такое, что <math>l_v <_1 x <_1 r_v \;</math>, либо существует некоторое <math>x \in N(v) \;</math>, такое, что <math>l_u <_1 x <_1 r_u \;</math>. В противном случае они называются подходящими. Заметим, что для подходящих <math>\{ u, v \} \;</math> верно <math>c_{uv} \cdot c_{vu} = 0 \;</math>. Джумович и Уайтсайдз показали: | ||
'''Лемма 5 ([5])'''. При любом оптимальном отношении порядка <math><_2 \;</math> на вершинах <math>V_2 \;</math>, <math>u <_2 v \;</math> найдено, если <math>r_u \le_1 l_v \;</math>. | '''Лемма 5 ([5])'''. При любом оптимальном отношении порядка <math><_2 \;</math> на вершинах <math>V_2 \;</math>, <math>u <_2 v \;</math> найдено, если <math>r_u \le_1 l_v \;</math>. | ||
Это означает, что все подходящие пары встречаются в своем естественном порядке. | Это означает, что все подходящие пары встречаются в своем ''естественном порядке''. | ||
| Строка 91: | Строка 91: | ||
Этот простой алгоритм поиска по дереву можно улучшить. Во-первых, отметим, что нет необходимости ветвления в {x, y} | Этот простой алгоритм поиска по дереву можно улучшить. Во-первых, отметим, что нет необходимости ветвления в <math>\{ x, y \} \subset V_2 \;</math>, если <math>c_{xy} = c_{yx} \;</math>. Это позволяет внести две модификации в Алгоритм 1: | ||
• На строке 5 следует исключить <math>c_{xy} = c_{yx} \;</math>. | • На строке 5 следует исключить равенство <math>c_{xy} = c_{yx} \;</math>. | ||
• На строке 12 следует произвольным образом включить некоторую пару <math>\{ x, y \} \subset V_2 \;</math>, которая еще не была включена, и рекурсивно повторять это действие; только если включены все пары <math>\{ x, y \} \subset V_2 \;</math>, следует вернуть значение ДА. | • На строке 12 следует произвольным образом включить некоторую пару <math>\{ x, y \} \subset V_2 \;</math>, которая еще не была включена, и рекурсивно повторять это действие; только если включены все пары <math>\{ x, y \} \subset V_2 \;</math>, следует вернуть значение ДА. | ||
| Строка 100: | Строка 100: | ||
В результате модификаций получен алгоритм решения задачи OSCM с параметром <math>O^*(1,6182^k) \;</math>. Он составляет ядро алгоритма Джумовича и Уайтсайдза [5]. В их работе более детально обсуждаются следующие вопросы: | В результате модификаций получен алгоритм решения задачи OSCM с параметром <math>O^*(1,6182^k) \;</math>. Он составляет ядро алгоритма Джумовича и Уайтсайдза [5]. В их работе более детально обсуждаются следующие вопросы: | ||
• Как эффективно вычислить все количества пересечений | • Как эффективно вычислить все количества пересечений <math>c_{xy} \;</math> на этапе предварительной обработки? | ||
• Как интегрировать в алгоритм элементы ветвления и обрезки, полезные с практической точки зрения? | • Как интегрировать в алгоритм элементы ветвления и обрезки, полезные с практической точки зрения? | ||
| Строка 110: | Строка 110: | ||
'''Теорема 7. Задачу односторонней минимизации пересечений можно решить за время <math>O^*( | '''Теорема 7. Задачу односторонней минимизации пересечений можно решить за время <math>O^*(1,4656^k) \;</math>.''' | ||
Возможный вариант | Возможный вариант выполнения улучшенного алгоритма поиска по дереву приведен на рис. 2, а его (оптимальный) результат – на рис. 3. | ||
| Строка 134: | Строка 134: | ||
'''Варианты этой задачи и родственные ей проблемы''' широко рассматривались в литературе. | '''Варианты этой задачи и родственные ей проблемы''' широко рассматривались в литературе. | ||
1. Изменение цели оптимизации: минимизация количества дуг, участвующих в пересечениях – одноуровневая планаризация. Как было отмечено в [7, 10], из теоремы 2 практически непосредственно следует идея алгоритма решения этой задачи с временем | 1. Изменение цели оптимизации: минимизация количества дуг, участвующих в пересечениях – одноуровневая планаризация. Как было отмечено в [7, 10], из теоремы 2 практически непосредственно следует идея алгоритма решения этой задачи с временем выполнения <math>O^*(3^k) \;</math>, которое впоследствии было улучшено в [10] до <math>O^*(2^k) \;</math>. | ||
2. Можно повысить число степеней свободы, рассматривая два или более уровня присваиваний в одно и то же время. Параметризованные алгоритмы для минимизации пересечений и для планаризации были предложены в [3, 7, 10]. | 2. Можно повысить число степеней свободы, рассматривая два или более уровня присваиваний в одно и то же время. Параметризованные алгоритмы для минимизации пересечений и для планаризации были предложены в [3, 7, 10]. | ||
| Строка 141: | Строка 141: | ||
== Применение == | == Применение == | ||
Помимо рассмотрения вопроса графического построения двудольных графов как задачи, интересной самой по себе ( | Помимо рассмотрения вопроса графического построения двудольных графов как задачи, интересной самой по себе (например, для качественного изображения диаграмм отношений), этот вопрос естественным образом возникает при применении так называемого подхода Судзиямы к построению иерархических графов [12]. Этот исключительно популярный подход решает задачу укладки иерархического графа в три этапа: (1) удаление циклов, (2) присваивание вершин уровням, (3) присваивание вершин уровням. Последний этап обычно реализуется посредством алгоритма с заметающей прямой, в процессе работы решающего несколько экземпляров задачи односторонней минимизации пересечений. Третий вариант задачи, упомянутый выше, находит множество важных вариантов применения в вычислительной биологии. | ||
== Открытые вопросы == | == Открытые вопросы == | ||
Как и для всех алгоритмов с экспоненциальным временем | Как и для всех алгоритмов с экспоненциальным временем выполнения, оказывается непросто улучшить это время или доказать определенную нижнюю границу времени выполнения при наличии разумных теоретико-сложностных предположений. Заметим, что негласные предположения, лежащие в основе подхода параметризованных алгоритмов, в данном сценарии полностью удовлетворяются: к примеру, графическое представление с большим количеством пересечений будет неприемлемым (если такая ситуация встретится на практике, придется прибегнуть к другому способу представления информации); таким образом, можно обоснованно предполагать, что параметр действительно окажется малым. | ||
| Строка 184: | Строка 183: | ||
12. Sugiyama, K., Tagawa, S., Toda, M.: Methods for visual understanding of hierarchical system structures. IEEE Trans. Syst. Man Cybernet. 11 (2), 109-125 (1981) | 12. Sugiyama, K., Tagawa, S., Toda, M.: Methods for visual understanding of hierarchical system structures. IEEE Trans. Syst. Man Cybernet. 11 (2), 109-125 (1981) | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 04:41, 22 ноября 2024
Постановка задачи
Задача односторонней минимизации пересечений (One-sided crossing minimization, OSCM) может рассматриваться как некоторая форма построения двудольного графа [math]\displaystyle{ G = (V_1, V_2, \; E) }[/math], у которого все вершины из разбиения [math]\displaystyle{ V_i \; }[/math] присвоены к одной и той же линии (также называемой уровнем) [math]\displaystyle{ L_i \; }[/math] на плоскости, при этом линии [math]\displaystyle{ L_1 \; }[/math] и [math]\displaystyle{ L_2 \; }[/math] параллельны. Присваивание вершин к линии [math]\displaystyle{ L_1 \; }[/math] фиксировано; присваивание к линии [math]\displaystyle{ L_2 \; }[/math] свободно и выбирается таким образом, чтобы минимизировать количество пересечений между ребрами, представленными в виде отрезков прямых.
Нотация
Граф G описывается множеством его вершин V и ребер E, т.е. G = (V, E), где [math]\displaystyle{ E \subseteq V \times V \; }[/math]. Обозначим за [math]\displaystyle{ N(v) \; }[/math] (открытую) окрестность вершины v, включающую все вершины, смежные с v; за [math]\displaystyle{ N[v] = N(v) \cup \{ v \} \; }[/math] – закрытую окрестность v; за [math]\displaystyle{ deg(v) = |N(v)| \; }[/math] – степень вершины v. Для множества вершин S, [math]\displaystyle{ N(S) = \bigcup_{v \in S} N(v) \; }[/math] и [math]\displaystyle{ N[S] = N(S) \cup S \; }[/math]. [math]\displaystyle{ G[S] \; }[/math] обозначает граф, порожденный множеством вершин S, т.е. [math]\displaystyle{ G[S] = (S, E \cap (S \times S)) \; }[/math]. Граф G = (V, E) с множеством вершин V и множеством дуг [math]\displaystyle{ E \subseteq V \times V \; }[/math] является двудольным, если существует разбиение [math]\displaystyle{ V \; }[/math] на два множества [math]\displaystyle{ V_1 \; }[/math] и [math]\displaystyle{ V_2 \; }[/math], такие, что [math]\displaystyle{ V = V_1 \cup V_2 \; }[/math], [math]\displaystyle{ V_1 \cap V_2 = \empty \; }[/math] и [math]\displaystyle{ E \subseteq V_1 \times V_2 \; }[/math]. Для наглядности запишем это в следующем виде: [math]\displaystyle{ G = (V_1, V_2, E) \; }[/math].
Двухуровневое графическое представление двудольного графа G = [math]\displaystyle{ (V_1, V_2, E) \; }[/math] может быть описано при помощи двух отношений линейного порядка: [math]\displaystyle{ \lt _1 \; }[/math] на [math]\displaystyle{ V_1 \; }[/math] и [math]\displaystyle{ \lt _2 \; }[/math] на [math]\displaystyle{ V_2 \; }[/math]. Это представление можно реализовать следующим образом: вершины из подмножества [math]\displaystyle{ V_1 \; }[/math] располагаются на линии [math]\displaystyle{ L_1 \; }[/math] (также называемой уровнем) в порядке, порождаемом отношением [math]\displaystyle{ \lt _1 \; }[/math], а вершины из [math]\displaystyle{ V_2 \; }[/math] располагаются на втором уровне [math]\displaystyle{ L_2 \; }[/math], параллельном первому, в порядке, порождаемом отношением [math]\displaystyle{ \lt _2 \; }[/math]; затем следует изобразить прямолинейный отрезок для каждого ребра [math]\displaystyle{ e = (u_1, u_2) \; }[/math] из E, соединяющий точки, представляющие [math]\displaystyle{ u_1 \; }[/math] и [math]\displaystyle{ u_2 \; }[/math], соответственно. Пересечение представляет собой пару ребер [math]\displaystyle{ e = (u_1, u_2) \; }[/math] и [math]\displaystyle{ f = (v_1, v_2) \; }[/math], имеющих общую точку в реализации двухуровневого графического представления [math]\displaystyle{ (G, \lt _1, \lt _2) \; }[/math]. Хорошо известно, что два ребра пересекаются в том и только том случае, если [math]\displaystyle{ u_1 \lt _1 v_1 \; }[/math] и [math]\displaystyle{ v_2 \lt _2 u_2 \; }[/math]; иными словами, это понятие несет чисто комбинаторный смысл, не зависящий от конкретной реализации двухуровневого графического представления. Обозначим за [math]\displaystyle{ cr(G, \lt _1, \lt _2) \; }[/math] количество пересечений в описываемом двухуровневом представлении. В контексте представления графов, разумеется, очень желательно получить минимальное число пересечений. В самой простой (и, вероятно, самой важной) форме это выглядит следующим образом: порядок вершин на одном уровне фиксируется, задача заключается в минимизации количества пересечений путем выбора порядка на втором уровне. Более формально:
Задача 1 (k-OSCM)
Дано: простой двудольный граф с n вершинами [math]\displaystyle{ G = (V_1, V_2, E) \; }[/math] и отношение линейного порядка [math]\displaystyle{ \lt _1 \; }[/math] на [math]\displaystyle{ V_1 \; }[/math]; неотрицательное целое число k (параметр).
Требуется: если это возможно, найти такой линейный порядок [math]\displaystyle{ \lt _2 \; }[/math] на [math]\displaystyle{ V_2 \; }[/math], что [math]\displaystyle{ cr(G, \lt _1, \lt _2) \le k \; }[/math]. Если такого линейного порядка не существует, алгоритм должен выдать соответствующее сообщение.
Возьмем для примера [math]\displaystyle{ G = (V_1, V_2, E) \; }[/math] и [math]\displaystyle{ \lt _1 \; }[/math] из задачи односторонней минимизации пересечений (OSCM) и две вершины [math]\displaystyle{ u, v \in V_2 \; }[/math],
[math]\displaystyle{ c_{uv} =cr(G[N[ \{ u, v \} ]], \lt _1 \cap (N( \{ u, v \} ) \times N( \{ u, v \} )), \{ (u, v) \} ) \;. }[/math]
Таким образом, при выборе упорядочения [math]\displaystyle{ u \lt _2 v \; }[/math] необходимо рассматривать замкнутые окрестности u и v.
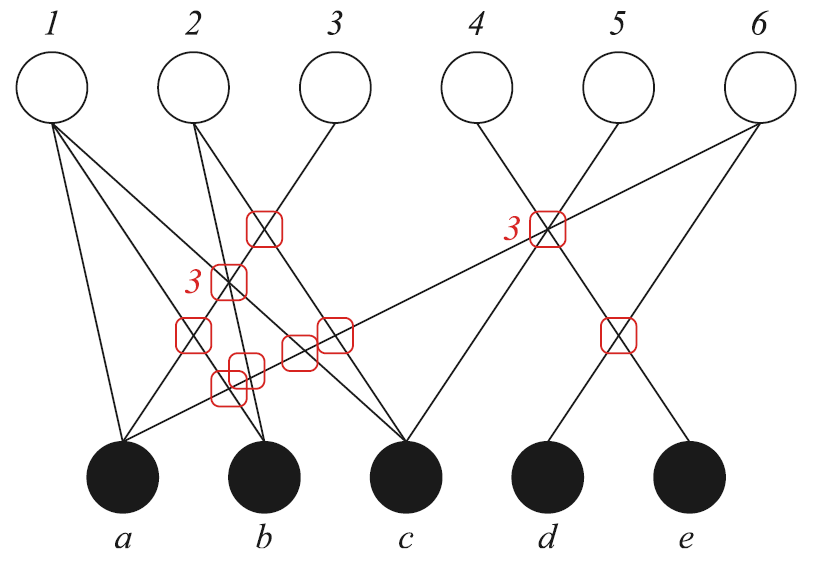
На рис. 1 приведен пример конкретного графического представления двудольного графа. Является ли это представление оптимальным в смысле количества пересечений, предполагая, что порядок верхнего уровня фиксирован? В случаях, когда пересекаются более двух ребер, на рисунке указано количество пересечений. Все пересечения отмечены красными квадратами.
Рис. 1. Пример графа из задачи односторонней минимизации пересечений.
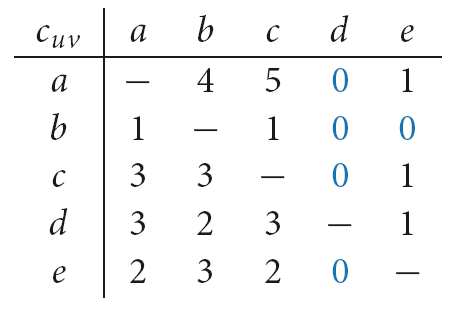
Вычислим матрицу количества пересечений ([math]\displaystyle{ c_{uv} \; }[/math]) для этого графа.
Количество пересечений в данном графическом представлении может быть вычислено следующим образом:
[math]\displaystyle{ c_{ab} + c_{ac} + c_{ad} + c_{ae} + c_{bc} + c_{bd} + c_{be} + c_{cd} + c_{ce} + c_{de} = 13 \; }[/math].
Основные результаты
Для задач, для которых не предполагается существования полиномиальных алгоритмов, очень желательно найти точные алгоритмы с экспоненциальным временем выполнения.
Теорема 1 ([6]). Задача разрешимости, соответствующая k-OSCM, является NP-полной.
Далее будем предполагать, что [math]\displaystyle{ G = (V_1, V_2, E) \; }[/math] – экземпляр задачи OSCM с фиксированным порядком [math]\displaystyle{ \lt _1 \; }[/math] на [math]\displaystyle{ V_1 \; }[/math].
Проверить, существует ли порядок на [math]\displaystyle{ V_2 \; }[/math], позволяющий избежать пересечений, можно за полиномиальное время. Это наблюдение основывается на одной из следующих теоретико-графовых характеристик:
Теорема 2 ([3]). [math]\displaystyle{ cr(G, \lt _1, \lt _2) = 0 \; }[/math] в том и только том случае, если G является ациклическим и для любого пути (x, a, y) в G, [math]\displaystyle{ x, y \in V_1 \; }[/math], выполняется следующее: для всех [math]\displaystyle{ u \in V_1 \; }[/math] при [math]\displaystyle{ x \lt _1 u \lt _1 y \; }[/math] единственным ребром, инцидентным u, если таковое существует, является (u, a).
Ранее введенное понятие является критически важным по следующим причинам:
Лемма 3. [math]\displaystyle{ \sum_{u, v \in V_2, u \lt _2 v} c_{uv} = cr(G, \lt _1, \lt _2) \; }[/math].
Теорема 4 ([9]). Если k – минимальное количество пересечений ребер в экземпляре задачи OSCM [math]\displaystyle{ (G = (V_1, V_2, E), \lt _1 )\; }[/math], то [math]\displaystyle{ \sum_{u, v \in V_2, u \ne v} min \{ c_{uv}, v_{vu} \} \le k \lt 1,4664 \sum_{u, v \in V_2, u \ne v} min \{ c_{uv}, v_{vu} \} \; }[/math].
Нагамочи предложил аппроксимационный алгоритм с коэффициентом меньше 1,4664.
Далее, для любой вершины [math]\displaystyle{ u \in V_2 \; }[/math] с [math]\displaystyle{ deg(u) \gt 0 \; }[/math] обозначим за [math]\displaystyle{ l_u \; }[/math] самого левого соседа u в [math]\displaystyle{ L_1 \; }[/math], а за [math]\displaystyle{ r_u \; }[/math] – самого правого. Две вершины [math]\displaystyle{ u, v \in V_2 \; }[/math] называются неподходящими, если существует некоторое [math]\displaystyle{ x \in N(u) \; }[/math], такое, что [math]\displaystyle{ l_v \lt _1 x \lt _1 r_v \; }[/math], либо существует некоторое [math]\displaystyle{ x \in N(v) \; }[/math], такое, что [math]\displaystyle{ l_u \lt _1 x \lt _1 r_u \; }[/math]. В противном случае они называются подходящими. Заметим, что для подходящих [math]\displaystyle{ \{ u, v \} \; }[/math] верно [math]\displaystyle{ c_{uv} \cdot c_{vu} = 0 \; }[/math]. Джумович и Уайтсайдз показали:
Лемма 5 ([5]). При любом оптимальном отношении порядка [math]\displaystyle{ \lt _2 \; }[/math] на вершинах [math]\displaystyle{ V_2 \; }[/math], [math]\displaystyle{ u \lt _2 v \; }[/math] найдено, если [math]\displaystyle{ r_u \le_1 l_v \; }[/math].
Это означает, что все подходящие пары встречаются в своем естественном порядке.
Теперь можно сформулировать первый параметризованный алгоритм односторонней минимизации пересечений (OSCM), представляющий собой простой алгоритм поиска по дереву. По мере выполнения этого алгоритма последовательно строится подходящий порядок [math]\displaystyle{ \lt _2 \; }[/math] на [math]\displaystyle{ V_2 \; }[/math]; при установлении отношения порядка между u и v на [math]\displaystyle{ V_2 \; }[/math] в него будет включено [math]\displaystyle{ u \lt _2 v \; }[/math] или [math]\displaystyle{ v \lt _2 u \; }[/math]. Таким образом, обобщенный экземпляр задачи OSCM помимо двудольного графа [math]\displaystyle{ G = (V_1, V_2, E) \; }[/math] содержит отношение частичного порядка [math]\displaystyle{ \lt _2 \; }[/math] на [math]\displaystyle{ V_2 \; }[/math]. Вершина [math]\displaystyle{ v \in V_2 \; }[/math] полностью включена, если для всех [math]\displaystyle{ u \in V_2 \backslash \{ u, v \} \; }[/math] пара [math]\displaystyle{ \{ u, v \} \; }[/math] включена.
Лемма 5 позволяет сформулировать следующее правило:
Правило RR1: Для каждой пары вершин {u, v} из [math]\displaystyle{ V_2 \; }[/math] с [math]\displaystyle{ c_{uv} = 0 \; }[/math] включить [math]\displaystyle{ u \lt _2 v \; }[/math]. В приведенном примере d будет полностью включено в результате применения правила RR1, поскольку столбец d в матрице пересечений заполнен нулями; следовательно, в последующих действиях d можно игнорировать.
Алгоритм 1 представляет собой простой алгоритм поиска по дереву для задачи OSCM, последовательно применяющий правило RR1.
Лемма 6. OSCM можно вычислить за время [math]\displaystyle{ 0^*(2^k) \; }[/math].
Доказательство. До того, как будет производиться какое-либо ветвление, выполняется редукция экземпляра графа таким образом, чтобы любая невключенная пара вершин {u, v} из [math]\displaystyle{ V_2 \; }[/math] удовлетворяла условию [math]\displaystyle{ min \{ c_{uv}, c_{vu} \} \ge 1 \; }[/math]. Следовательно, каждое рекурсивное ветвление уменьшает параметр как минимум на 1.□
Этот простой алгоритм поиска по дереву можно улучшить. Во-первых, отметим, что нет необходимости ветвления в [math]\displaystyle{ \{ x, y \} \subset V_2 \; }[/math], если [math]\displaystyle{ c_{xy} = c_{yx} \; }[/math]. Это позволяет внести две модификации в Алгоритм 1:
• На строке 5 следует исключить равенство [math]\displaystyle{ c_{xy} = c_{yx} \; }[/math].
• На строке 12 следует произвольным образом включить некоторую пару [math]\displaystyle{ \{ x, y \} \subset V_2 \; }[/math], которая еще не была включена, и рекурсивно повторять это действие; только если включены все пары [math]\displaystyle{ \{ x, y \} \subset V_2 \; }[/math], следует вернуть значение ДА.
В результате модификаций получен алгоритм решения задачи OSCM с параметром [math]\displaystyle{ O^*(1,6182^k) \; }[/math]. Он составляет ядро алгоритма Джумовича и Уайтсайдза [5]. В их работе более детально обсуждаются следующие вопросы:
• Как эффективно вычислить все количества пересечений [math]\displaystyle{ c_{xy} \; }[/math] на этапе предварительной обработки?
• Как интегрировать в алгоритм элементы ветвления и обрезки, полезные с практической точки зрения?
• Как обобщить алгоритм для экземпляров, допускающих наличие целочисленных весов у ребер (параллельных ребер)?
Дальнейшие улучшения возможны в результате более глубокого анализа локальных паттернов [math]\displaystyle{ \{ x, y \} \in V_2 \; }[/math], таких, что [math]\displaystyle{ c_{xy} c_{yx} \le 2 \; }[/math]. Таким образом было показано:
Теорема 7. Задачу односторонней минимизации пересечений можно решить за время [math]\displaystyle{ O^*(1,4656^k) \; }[/math].
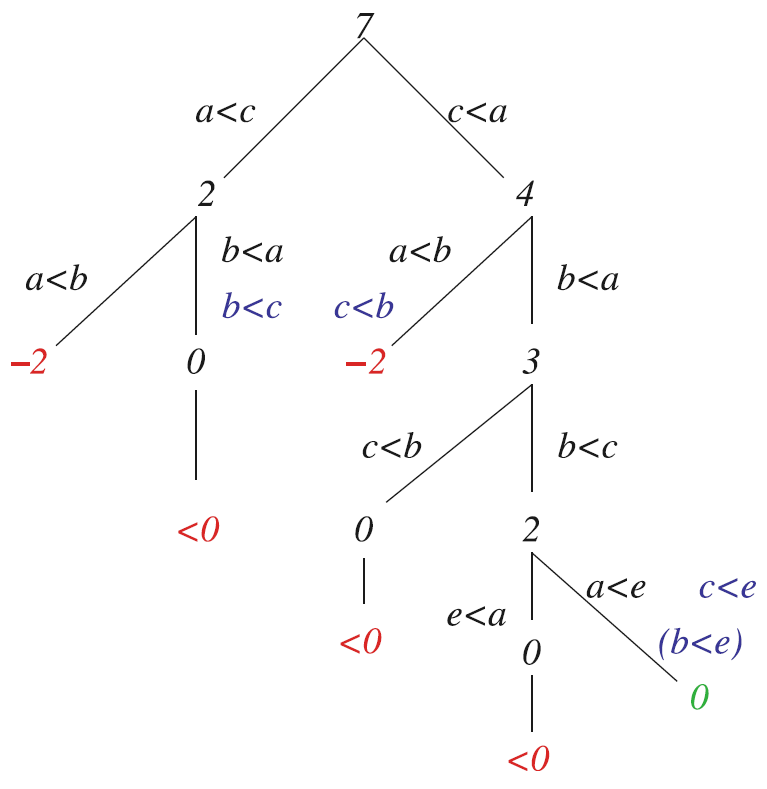
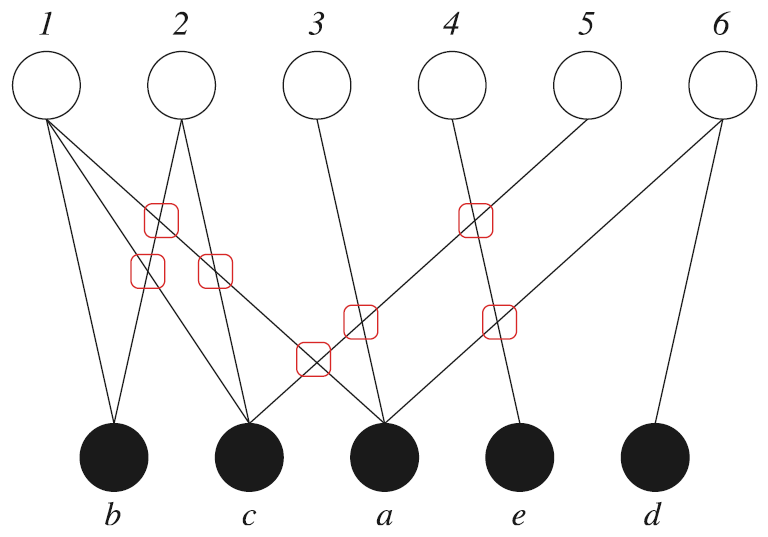
Возможный вариант выполнения улучшенного алгоритма поиска по дереву приведен на рис. 2, а его (оптимальный) результат – на рис. 3.
Алгоритм 1. Алгоритм OSCM-ST-simple поиска по дереву для задачи OSCM
Рис. 2. Пример дерева поиска для задачи OSCM
Рис. 3. Оптимальное решение для экземпляра задачи
Варианты этой задачи и родственные ей проблемы широко рассматривались в литературе.
1. Изменение цели оптимизации: минимизация количества дуг, участвующих в пересечениях – одноуровневая планаризация. Как было отмечено в [7, 10], из теоремы 2 практически непосредственно следует идея алгоритма решения этой задачи с временем выполнения [math]\displaystyle{ O^*(3^k) \; }[/math], которое впоследствии было улучшено в [10] до [math]\displaystyle{ O^*(2^k) \; }[/math].
2. Можно повысить число степеней свободы, рассматривая два или более уровня присваиваний в одно и то же время. Параметризованные алгоритмы для минимизации пересечений и для планаризации были предложены в [3, 7, 10].
3. Можно рассмотреть другие дополнительные ограничения на графическое построение или допустимые отношения порядка; так, в [8] были рассмотрены параметризованные алгоритмы для задачи двухуровневого присваивания, в которой допустимые отношения порядка были ограничены бинарными деревьями.
Применение
Помимо рассмотрения вопроса графического построения двудольных графов как задачи, интересной самой по себе (например, для качественного изображения диаграмм отношений), этот вопрос естественным образом возникает при применении так называемого подхода Судзиямы к построению иерархических графов [12]. Этот исключительно популярный подход решает задачу укладки иерархического графа в три этапа: (1) удаление циклов, (2) присваивание вершин уровням, (3) присваивание вершин уровням. Последний этап обычно реализуется посредством алгоритма с заметающей прямой, в процессе работы решающего несколько экземпляров задачи односторонней минимизации пересечений. Третий вариант задачи, упомянутый выше, находит множество важных вариантов применения в вычислительной биологии.
Открытые вопросы
Как и для всех алгоритмов с экспоненциальным временем выполнения, оказывается непросто улучшить это время или доказать определенную нижнюю границу времени выполнения при наличии разумных теоретико-сложностных предположений. Заметим, что негласные предположения, лежащие в основе подхода параметризованных алгоритмов, в данном сценарии полностью удовлетворяются: к примеру, графическое представление с большим количеством пересечений будет неприемлемым (если такая ситуация встретится на практике, придется прибегнуть к другому способу представления информации); таким образом, можно обоснованно предполагать, что параметр действительно окажется малым.
Это верно также для других NP-полных подзадач, относящихся к подходу Судзиямы. Однако на наличие простых решений рассчитывать не стоит. Например, для задачи построения множества ориентированных обратных дуг [1], эквивалентной первой фазе, неизвестно о существовании подходящего параметризованного алгоритма [2].
Экспериментальные результаты
Садермен [10] провел эксперименты практически со всеми вариантами данной задачи; в [11] некоторые из экспериментальных результатов представлены в более наглядной форме.
Ссылка на код
Несколько JAVA-апплетов для решения задач, упомянутых в данной статье, приведены Садерменом на http://cgm.cs.mcgill.ca/~msuder/.
См. также
Другие параметризованные алгоритмы поиска по дереву можно найти в совместной работе «Деревья поиска в задаче о вершинном покрытии» (Чен, Кань, Цзя).
Литература
1. Chen, J., Liu, Y., Lu, S., O'Sullivan, B., Razgon, I.: A Fixed-Parameter Algorithm for the Directed Feedback Vertex Set Problem. In: 40th ACM Symposium on Theory of Computing STOC 2008, May 17-20, Victoria (BC), Canada (2008)
2. Downey, R.G., Fellows, M.R.: Parameterized Complexity. Springer, Berlin (1999)
3. Dujmovic, V., Fellows, M.R., Hallett, M., Kitching, M., Liotta, G., McCartin, C., Nishimura, N., Ragde, P., Rosamond, F.A., Suderman, M., Whitesides, S., Wood, D.R.: A fixed-parameter approach to 2-layer planarization. Algorithmica 45, 159-182 (2006)
4. Dujmovic, V., Fernau, H., Kaufmann, M.: Fixed parameter algorithms for one-sided crossing minimization revisited. In: Liotta G. (ed.) Graph Drawing, 11th International Symposium GD 2003. LNCS, vol. 2912, pp. 332-344. Springer, Berlin (2004). A journal version has been accepted to J. Discret. Algorithms, see doi: 10.1016/j.jda.2006.12.008
5. Dujmovic, V., Whitesides, S.: An efficient fixed parameter tractable algorithm for 1-sided crossing minimization. Algorithmica 40,15-32 (2004)
6. Eades, P., Wormald, N.C.: Edge crossings in drawings of bipartite graphs. Algorithmica 11, 379^03 (1994)
7. Fernau, H.: Two-layer planarization: improving on parameterized algorithmics. J. Graph Algorithms Appl. 9, 205-238 (2005)
8. Fernau, H., Kaufmann, M., Poths, M.: Comparing trees via crossing minimization. In: Ramanujam R., Sen S. (eds.) Foundations of Software Technology and Theoretical Computer Science FSTTCS 2005. LNCS, vol. 3821, pp. 457-469. Springer, Berlin (2005)
9. Nagamochi, H.: An improved bound on the one-sided minimum crossing number in two-layered drawings. Discret. Comput. Geom. 33,569-591 (2005)
10. Suderman, M.: Layered Graph Drawing. Ph.D. thesis, McGill University, Montreal (2005)
11. Suderman, M., Whitesides, S.: Experiments with the fixed-parameter approach for two-layer planarization. J. Graph Algorithms Appl. 9(1), 149-163 (2005)
12. Sugiyama, K., Tagawa, S., Toda, M.: Methods for visual understanding of hierarchical system structures. IEEE Trans. Syst. Man Cybernet. 11 (2), 109-125 (1981)