Автоматическая генерация дерева поиска: различия между версиями
Irina (обсуждение | вклад) |
KVN (обсуждение | вклад) |
||
| (не показано 10 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
Ключевые слова и синонимы: [[Автоматическое доказательство для верхней границы времени | Ключевые слова и синонимы: [[Автоматическое доказательство для верхней границы времени выполнения алгоритмов расщепления]] | ||
== Постановка задачи == | == Постановка задачи == | ||
Эта задача связана с автоматической разработкой и анализом алгоритмов для дерева поиска. Алгоритмы поиска по дереву представляют собой популярный способ нахождения оптимальных решений для NP-полных задач (для простоты изложения рассматриваются только проблемы разрешимости; адаптация для решения задач оптимизации тривиальна). Суть этого подхода заключается в рекурсивном решении нескольких экземпляров меньшего размера таким образом, что хотя бы одна из ветвей содержит положительный ответ в том и только том случае, если его содержит исходный экземпляр. Обычно это достигается путем перебора всех возможных способов присвоить сертификат решения некоторой малой порции входных данных с получением небольшой локальной модификации на экземпляре каждой ветви. | Эта задача связана с автоматической разработкой и анализом алгоритмов для дерева поиска. Алгоритмы поиска по дереву представляют собой популярный способ нахождения оптимальных решений для NP-полных задач (для простоты изложения рассматриваются только проблемы разрешимости; адаптация для решения задач оптимизации тривиальна). Суть этого подхода заключается в рекурсивном решении нескольких экземпляров меньшего размера таким образом, что хотя бы одна из ветвей содержит положительный ответ в том и только том случае, если его содержит исходный экземпляр. Обычно это достигается путем перебора всех возможных способов присвоить сертификат решения некоторой малой порции входных данных с получением небольшой локальной модификации на экземпляре каждой ветви. | ||
Рассмотрим, к примеру, NP-полную задачу перевода в кластеры (CLUSTER EDITING): можно ли модифицировать некоторый граф путем добавления или удаления не более k | Рассмотрим, к примеру, NP-полную '''задачу перевода в кластеры''' (''CLUSTER EDITING problem''): можно ли модифицировать некоторый граф путем добавления или удаления не более k ребер таким образом, чтобы полученный граф был '''кластерным графом''' (''cluster graph'') , или несвязным объединением [[Клика|клик]]? Чтобы создать алгоритм поиска по дереву для CLUSTER EDITING, следует использовать тот факт, что кластерные графы представляют собой графы, не содержащие <math>P_3</math> (путей с 3 вершинами) в качестве порожденного подграфа. Таким образом, решить задачу CLUSTER EDITING можно путем нахождения <math>P_3</math> и разделения его на три ветви следующим способом: удалить первое ребро, удалить второе ребро или добавить недостающее ребро. Согласно этой трактовке в случае, если <math>P_3</math> не найдено, мы имеем кластерный граф. Исходный экземпляр имеет решение с k модификациями в том и только том случае, если по меньшей мере одна из ветвей имеет решение с k – 1 модификациями. | ||
== Анализ == | == Анализ == | ||
Для NP-полных задач время работы алгоритма поиска по дереву зависит только от размера дерева поиска с точностью до полиномиального множителя, который, в свою очередь, зависит от количества ветвей и сокращения размера каждой ветви. Если алгоритм решает задачу размера s и рекурсивно вызывает себя для задач с размерами s - <math>d_1</math>, ..., s - <math>d_i</math>, тогда вектор <math>(d_1, ..., d_i)</math> называется | Для NP-полных задач время работы алгоритма поиска по дереву зависит только от размера дерева поиска с точностью до полиномиального множителя, который, в свою очередь, зависит от количества ветвей и сокращения размера каждой ветви. Если алгоритм решает задачу размера s и рекурсивно вызывает себя для задач с размерами s - <math>d_1</math>, ..., s - <math>d_i</math>, тогда вектор <math>(d_1, ..., d_i)</math> называется '''вектором ветвления''' (''branching vector'') данной рекурсии. Известно, что размер дерева поиска в таком случае составляет <math>O(\alpha^s) \, </math>, где α – '''коэффициент ветвления''' (''branching number'') – единственный действительный корень '''характеристического многочлена ('''''characteristic polynomial''''')''' | ||
<math>z^d \, </math> – <math>z^{d-d_1}</math> – ... – <math>z^{d-d_i}</math> (1) | <math>z^d \, </math> – <math>z^{d-d_1}</math> – ... – <math>z^{d-d_i}</math> (1) | ||
где d = max{<math>d_1, ..., d_i</math>}. Для простого алгоритма поиска по дереву CLUSTER EDITING и размера k вектор ветвления имеет значение (1,1,1), а коэффициент ветвления равен 3, что означает, что время | где d = max{<math>d_1, ..., d_i</math>}. Для простого алгоритма поиска по дереву CLUSTER EDITING и размера k вектор ветвления имеет значение (1,1,1), а коэффициент ветвления равен 3, что означает, что время выполнения содержит полиномиальный коэффициент <math>O(3^k) \,</math>. | ||
== Различение вариантов == | == Различение вариантов == | ||
Нередко время | Нередко время выполнения можно улучшить, если различать разные варианты экземпляров и производить ветвление отдельно для каждого варианта. В таком случае время выполнения будет определяться коэффициентом ветвления наихудшего варианта. В нескольких публикациях такие алгоритмы были получены вручную (например, дерево поиска размера <math>O(2.27^k) \, </math> для CLUSTER EDITING [4]); однако эту задачу можно автоматизировать. Сформулируем ее следующим образом: | ||
'''Задача | '''Задача.''' ''Алгоритм быстрого поиска по дереву'' '''('''''Fast search tree algorithm''''')''' | ||
'''Дано: NP-полная задача P и мера величины s(I) экземпляра I задачи P, где экземпляры I с s(I) = 0 могут быть решены за полиномиальное время.''' | '''Дано:''' ''NP-полная задача P и мера величины s(I) экземпляра I задачи P, где экземпляры I с s(I) = 0 могут быть решены за полиномиальное время'''''.''' | ||
'''Требуется:''' ''Разбить множество экземпляров P на варианты и для каждого варианта найти такое ветвление, чтобы максимальный коэффициент ветвления среди всех ветвлений был минимальным из возможных.'' | |||
| Строка 28: | Строка 29: | ||
Грэмм и коллеги [3] описали метод получения алгоритмов быстрого поиска по дереву для CLUSTER EDITING и родственных задач, в которых мерой величины является количество операций редактирования k. Чтобы различать разные варианты, подграфы нумеруются таким образом, чтобы каждый экземпляр заведомо содержал не менее одного из этих подграфов. В рамках этого подхода можно найти ветвление для определенного варианта. | Грэмм и коллеги [3] описали метод получения алгоритмов быстрого поиска по дереву для CLUSTER EDITING и родственных задач, в которых мерой величины является количество операций редактирования k. Чтобы различать разные варианты, подграфы нумеруются таким образом, чтобы каждый экземпляр заведомо содержал не менее одного из этих подграфов. В рамках этого подхода можно найти ветвление для определенного варианта. | ||
Стандартным способом систематического получения специализированных ветвлений для вариантов экземпляров является использование сочетания базового ветвления и правил редукции данных. Базовое ветвление представляет собой простейшую технику ветвления; правило редукции данных заменяет экземпляр эквивалентным ему по решению экземпляром меньшего размера за полиномиальное время. Для применения этого подхода к CLUSTER EDITING прежде всего требуется небольшая модификация задачи: мы будем рассматривать аннотированную версию, в которой | Стандартным способом систематического получения специализированных ветвлений для вариантов экземпляров является использование сочетания базового ветвления и правил редукции данных. '''Базовое ветвление''' (''basic branching'') представляет собой простейшую технику ветвления; '''правило редукции данных''' (''data reduction rule'') заменяет экземпляр эквивалентным ему по решению экземпляром меньшего размера за полиномиальное время. Для применения этого подхода к CLUSTER EDITING прежде всего требуется небольшая модификация задачи: мы будем рассматривать ''аннотированную'' версию, в которой ребро может быть помечено как ''неизменное'', а отсутствующее ребро – как ''запрещенное''. Любая аннотированная подобным образом пара вершин не подлежит последующему редактированию. Для пары вершин базовое ветвление попадает в один из двух вариантов – неизменное либо запрещенное (для одного из вариантов потребуется операция редактирования). Правила редукции заключаются в следующем: если два неизменных ребра являются смежными, третье ребро порождаемого ими треугольника также должно быть неизменным; если смежными являются неизменное и запрещенное ребра, третье ребро порождаемого ими треугольника должно быть запрещенным. | ||
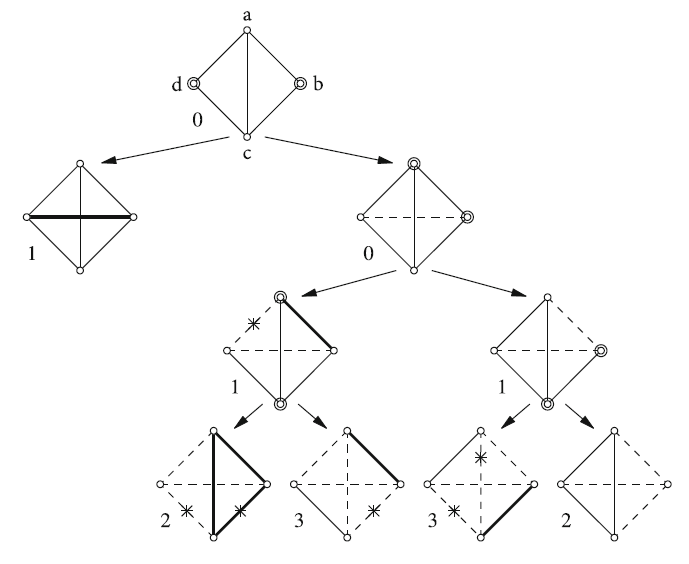
На рис. 1 представлен пример подобного ветвления. | На рис. 1 представлен пример подобного ветвления. | ||
Используя усовершенствованный метод поиска места для всех возможных вариантов и для различения всех ветвлений одного варианта, Грэмм и коллеги [3] разработали несколько алгоритмов поиска по дереву для задач модификации графов. | Используя усовершенствованный метод поиска места для всех возможных вариантов и для различения всех ветвлений одного варианта, Грэмм и коллеги [3] разработали несколько алгоритмов поиска по дереву для задач модификации графов. | ||
[[Файл:ASTG_pic1.png]] | |||
Автоматическая генерация дерева поиска, рис. 1 | Автоматическая генерация дерева поиска, рис. 1 | ||
Ветвление для варианта в алгоритме CLUSTER EDITING с использованием только базового ветвления на парах вершин (двойные круги) и применения правил редукции (звездочки). Неизменные ребра обозначены жирной линией, запрещенные – пунктирной. Числа около подграфов обозначают изменение размера задачи k. Вектор ветвления имеет значение (1,2,3,3,2), что соответствует размеру дерева поиска <math>O(2.27^k) \, </math> | |||
[[Файл:ASTG tab1.png]] | |||
Автоматическая генерация дерева поиска, таблица 1 | Автоматическая генерация дерева поиска, таблица 1 | ||
Сводные данные по размерам деревьев поиска, в которых автоматизация привела к улучшению. Сравниваются тривиальные, известные и новые алгоритмы. Под «известным» понимается лучшее из ранее опубликованных деревьев поиска, созданных вручную. Здесь m обозначает количество дизъюнктов, а l – длину формулы | |||
== Применение == | == Применение == | ||
| Строка 58: | Строка 53: | ||
== Открытые вопросы == | == Открытые вопросы == | ||
Анализ алгоритмов поиска по дереву можно значительно улучшить, если описывать «размер» экземпляра при помощи более чем одной переменной, что приводит к возникновению многовариантных рекуррентностей [1]. Использование этого подхода при автоматизированном написании алгоритмов пока еще является делом будущего. | Анализ алгоритмов поиска по дереву можно значительно улучшить, если описывать «размер» экземпляра при помощи более чем одной переменной, что приводит к возникновению многовариантных рекуррентностей [1]. Использование этого подхода при автоматизированном написании алгоритмов пока еще является делом будущего. | ||
Не раз отмечалось, что улучшенные временные границы, полученные в результате различения большего количества вариантов, не обязательно ускоряют | Не раз отмечалось, что улучшенные временные границы, полученные в результате различения большего количества вариантов, не обязательно ускоряют выполнение программы, но могут даже замедлить его. Тщательное изучение компромиссов, связанных с соответствующей адаптацией автоматизированных схем, еще ждет своих исследователей. | ||
Экспериментальные результаты | Экспериментальные результаты | ||
Грэмм и коллеги [3], а также Хиффнер [5] разработали алгоритмы поиска по дереву для нескольких NP-полных задач. Федин и Куликов [2] и Скъернаа [6] также добились результатов в нахождении удовлетворительных вариантов. Сводные данные приведены в таблице 1. | Грэмм и коллеги [3], а также Хиффнер [5] разработали алгоритмы поиска по дереву для нескольких NP-полных задач. Федин и Куликов [2] и Скъернаа [6] также добились результатов в нахождении удовлетворительных вариантов. Сводные данные приведены в таблице 1. | ||
== См. также == | |||
* ''[[Вершинное покрытие и деревья поиска]] | |||
== Литература == | == Литература == | ||
1. Eppstein, D.: Quasiconvex analysis of backtracking algorithms. In: Proc. 15th SODA, ACM/SIAM, pp. 788-797 (2004) | 1. Eppstein, D.: Quasiconvex analysis of backtracking algorithms. In: Proc. 15th SODA, ACM/SIAM, pp. 788-797 (2004) | ||
2. Fedin, S.S., Kulikov, A.S.: Automated proofs of upper bounds on the running time of splitting algorithms. J. Math. Sci. 134, 2383-2391 (2006). | 2. Fedin, S.S., Kulikov, A.S.: Automated proofs of upper bounds on the running time of splitting algorithms. J. Math. Sci. 134, 2383-2391 (2006). Улучшенные результаты можно найти по адресу по адресу http://logic.pdmi.ras.ru/~kulikov/autoproofs.html | ||
3. Gramm, J., Guo, J., HCiffner, F., Niedermeier, R.: Automated generation of search tree algorithms for hard graph modification problems. Algorithmica 39, 321-347 (2004) | 3. Gramm, J., Guo, J., HCiffner, F., Niedermeier, R.: Automated generation of search tree algorithms for hard graph modification problems. Algorithmica 39, 321-347 (2004) | ||
| Строка 79: | Строка 74: | ||
6. Skjernaa, B.: Exact Algorithms for Variants of Satisfiability and Colouring Problems. Ph. D. thesis, University of Aarhus, Department of Computer Science (2004) | 6. Skjernaa, B.: Exact Algorithms for Variants of Satisfiability and Colouring Problems. Ph. D. thesis, University of Aarhus, Department of Computer Science (2004) | ||
[[Категория: Совместное определение связанных терминов]] | |||
Текущая версия от 03:33, 22 ноября 2024
Ключевые слова и синонимы: Автоматическое доказательство для верхней границы времени выполнения алгоритмов расщепления
Постановка задачи
Эта задача связана с автоматической разработкой и анализом алгоритмов для дерева поиска. Алгоритмы поиска по дереву представляют собой популярный способ нахождения оптимальных решений для NP-полных задач (для простоты изложения рассматриваются только проблемы разрешимости; адаптация для решения задач оптимизации тривиальна). Суть этого подхода заключается в рекурсивном решении нескольких экземпляров меньшего размера таким образом, что хотя бы одна из ветвей содержит положительный ответ в том и только том случае, если его содержит исходный экземпляр. Обычно это достигается путем перебора всех возможных способов присвоить сертификат решения некоторой малой порции входных данных с получением небольшой локальной модификации на экземпляре каждой ветви.
Рассмотрим, к примеру, NP-полную задачу перевода в кластеры (CLUSTER EDITING problem): можно ли модифицировать некоторый граф путем добавления или удаления не более k ребер таким образом, чтобы полученный граф был кластерным графом (cluster graph) , или несвязным объединением клик? Чтобы создать алгоритм поиска по дереву для CLUSTER EDITING, следует использовать тот факт, что кластерные графы представляют собой графы, не содержащие [math]\displaystyle{ P_3 }[/math] (путей с 3 вершинами) в качестве порожденного подграфа. Таким образом, решить задачу CLUSTER EDITING можно путем нахождения [math]\displaystyle{ P_3 }[/math] и разделения его на три ветви следующим способом: удалить первое ребро, удалить второе ребро или добавить недостающее ребро. Согласно этой трактовке в случае, если [math]\displaystyle{ P_3 }[/math] не найдено, мы имеем кластерный граф. Исходный экземпляр имеет решение с k модификациями в том и только том случае, если по меньшей мере одна из ветвей имеет решение с k – 1 модификациями.
Анализ
Для NP-полных задач время работы алгоритма поиска по дереву зависит только от размера дерева поиска с точностью до полиномиального множителя, который, в свою очередь, зависит от количества ветвей и сокращения размера каждой ветви. Если алгоритм решает задачу размера s и рекурсивно вызывает себя для задач с размерами s - [math]\displaystyle{ d_1 }[/math], ..., s - [math]\displaystyle{ d_i }[/math], тогда вектор [math]\displaystyle{ (d_1, ..., d_i) }[/math] называется вектором ветвления (branching vector) данной рекурсии. Известно, что размер дерева поиска в таком случае составляет [math]\displaystyle{ O(\alpha^s) \, }[/math], где α – коэффициент ветвления (branching number) – единственный действительный корень характеристического многочлена (characteristic polynomial)
[math]\displaystyle{ z^d \, }[/math] – [math]\displaystyle{ z^{d-d_1} }[/math] – ... – [math]\displaystyle{ z^{d-d_i} }[/math] (1)
где d = max{[math]\displaystyle{ d_1, ..., d_i }[/math]}. Для простого алгоритма поиска по дереву CLUSTER EDITING и размера k вектор ветвления имеет значение (1,1,1), а коэффициент ветвления равен 3, что означает, что время выполнения содержит полиномиальный коэффициент [math]\displaystyle{ O(3^k) \, }[/math].
Различение вариантов
Нередко время выполнения можно улучшить, если различать разные варианты экземпляров и производить ветвление отдельно для каждого варианта. В таком случае время выполнения будет определяться коэффициентом ветвления наихудшего варианта. В нескольких публикациях такие алгоритмы были получены вручную (например, дерево поиска размера [math]\displaystyle{ O(2.27^k) \, }[/math] для CLUSTER EDITING [4]); однако эту задачу можно автоматизировать. Сформулируем ее следующим образом:
Задача. Алгоритм быстрого поиска по дереву (Fast search tree algorithm)
Дано: NP-полная задача P и мера величины s(I) экземпляра I задачи P, где экземпляры I с s(I) = 0 могут быть решены за полиномиальное время.
Требуется: Разбить множество экземпляров P на варианты и для каждого варианта найти такое ветвление, чтобы максимальный коэффициент ветвления среди всех ветвлений был минимальным из возможных.
Это определение задачи не вполне конкретно; в частности, необходимо иметь возможность быстро распознать вариант, к которому принадлежит экземпляр. Также неясно, существует ли оптимальный алгоритм поиска по дереву; можно полагать, что коэффициент ветвления можно последовательно уменьшать, повышая сложность различения вариантов.
Основные результаты
Грэмм и коллеги [3] описали метод получения алгоритмов быстрого поиска по дереву для CLUSTER EDITING и родственных задач, в которых мерой величины является количество операций редактирования k. Чтобы различать разные варианты, подграфы нумеруются таким образом, чтобы каждый экземпляр заведомо содержал не менее одного из этих подграфов. В рамках этого подхода можно найти ветвление для определенного варианта.
Стандартным способом систематического получения специализированных ветвлений для вариантов экземпляров является использование сочетания базового ветвления и правил редукции данных. Базовое ветвление (basic branching) представляет собой простейшую технику ветвления; правило редукции данных (data reduction rule) заменяет экземпляр эквивалентным ему по решению экземпляром меньшего размера за полиномиальное время. Для применения этого подхода к CLUSTER EDITING прежде всего требуется небольшая модификация задачи: мы будем рассматривать аннотированную версию, в которой ребро может быть помечено как неизменное, а отсутствующее ребро – как запрещенное. Любая аннотированная подобным образом пара вершин не подлежит последующему редактированию. Для пары вершин базовое ветвление попадает в один из двух вариантов – неизменное либо запрещенное (для одного из вариантов потребуется операция редактирования). Правила редукции заключаются в следующем: если два неизменных ребра являются смежными, третье ребро порождаемого ими треугольника также должно быть неизменным; если смежными являются неизменное и запрещенное ребра, третье ребро порождаемого ими треугольника должно быть запрещенным. На рис. 1 представлен пример подобного ветвления. Используя усовершенствованный метод поиска места для всех возможных вариантов и для различения всех ветвлений одного варианта, Грэмм и коллеги [3] разработали несколько алгоритмов поиска по дереву для задач модификации графов.
Автоматическая генерация дерева поиска, рис. 1
Ветвление для варианта в алгоритме CLUSTER EDITING с использованием только базового ветвления на парах вершин (двойные круги) и применения правил редукции (звездочки). Неизменные ребра обозначены жирной линией, запрещенные – пунктирной. Числа около подграфов обозначают изменение размера задачи k. Вектор ветвления имеет значение (1,2,3,3,2), что соответствует размеру дерева поиска [math]\displaystyle{ O(2.27^k) \, }[/math]
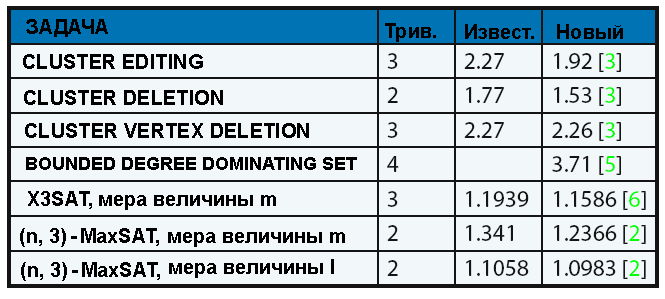
Автоматическая генерация дерева поиска, таблица 1
Сводные данные по размерам деревьев поиска, в которых автоматизация привела к улучшению. Сравниваются тривиальные, известные и новые алгоритмы. Под «известным» понимается лучшее из ранее опубликованных деревьев поиска, созданных вручную. Здесь m обозначает количество дизъюнктов, а l – длину формулы
Применение
Грамметал [3] применял автоматизированное создание алгоритмов поиска по дереву для нескольких задач модификации графов (см. также таблицу 1). Хиффнер [5] продемонстрировал применение алгоритма DOMINATING SET на графах степенью не выше 4, при этом мерой величины является размер доминирующего множества.
Федин и Куликов [2] исследовали варианты алгоритма SAT; однако в их работе была доказана только верхняя граница для фиксированного алгоритма, сами же алгоритмы не строились. Скьернаа [6] также представил результаты различных вариантов алгоритма SAT; его подход не требует введения пользователем правил редукции данных – они определяются автоматически.
Открытые вопросы
Анализ алгоритмов поиска по дереву можно значительно улучшить, если описывать «размер» экземпляра при помощи более чем одной переменной, что приводит к возникновению многовариантных рекуррентностей [1]. Использование этого подхода при автоматизированном написании алгоритмов пока еще является делом будущего. Не раз отмечалось, что улучшенные временные границы, полученные в результате различения большего количества вариантов, не обязательно ускоряют выполнение программы, но могут даже замедлить его. Тщательное изучение компромиссов, связанных с соответствующей адаптацией автоматизированных схем, еще ждет своих исследователей.
Экспериментальные результаты Грэмм и коллеги [3], а также Хиффнер [5] разработали алгоритмы поиска по дереву для нескольких NP-полных задач. Федин и Куликов [2] и Скъернаа [6] также добились результатов в нахождении удовлетворительных вариантов. Сводные данные приведены в таблице 1.
См. также
Литература
1. Eppstein, D.: Quasiconvex analysis of backtracking algorithms. In: Proc. 15th SODA, ACM/SIAM, pp. 788-797 (2004)
2. Fedin, S.S., Kulikov, A.S.: Automated proofs of upper bounds on the running time of splitting algorithms. J. Math. Sci. 134, 2383-2391 (2006). Улучшенные результаты можно найти по адресу по адресу http://logic.pdmi.ras.ru/~kulikov/autoproofs.html
3. Gramm, J., Guo, J., HCiffner, F., Niedermeier, R.: Automated generation of search tree algorithms for hard graph modification problems. Algorithmica 39, 321-347 (2004)
4. Gramm, J., Guo, J., HCiffner, F., Niedermeier, R.: Graph-modeled data clustering: Exact algorithms for clique generation. Theor. Comput. Syst. 38, 373-392 (2005)
5. HCiffner, F.: Graph Modification Problems and Automated Search Tree Generation. Diplomarbeit, Wilhelm-Schickard-Institut fur Informatik, Universitat Tubingen (2003)
6. Skjernaa, B.: Exact Algorithms for Variants of Satisfiability and Colouring Problems. Ph. D. thesis, University of Aarhus, Department of Computer Science (2004)