Конечный автомат: различия между версиями
KVN (обсуждение | вклад) м (Защищена страница «Конечный автомат» ([edit=autoconfirmed] (бессрочно) [move=autoconfirmed] (бессрочно))) |
KVN (обсуждение | вклад) Нет описания правки |
||
| Строка 22: | Строка 22: | ||
<math>M=(Q,\Sigma,\delta,q_0,F)</math>, в которой | <math>M=(Q,\Sigma,\delta,q_0,F)</math>, в которой | ||
(1) <math>Q</math> --- конечное множество ''состояний''; | (1) <math>Q</math> --- конечное множество [[Состояние автомата|''состояний'']]; | ||
(2) <math>\Sigma</math> --- конечное множество допустимых ''входных | (2) <math>\Sigma</math> --- конечное множество допустимых ''входных | ||
| Строка 30: | Строка 30: | ||
множество подмножеств <math>Q</math>, называемое ''функцией переходов''; | множество подмножеств <math>Q</math>, называемое ''функцией переходов''; | ||
(4) <math>q_0\in Q</math> --- выделенное ''начальное состояние''; | (4) <math>q_0\in Q</math> --- выделенное [[Начальное состояние автомата|''начальное состояние'']]; | ||
(5) <math>F\subseteq Q</math> --- множество ''заключительных состояний''. | (5) <math>F\subseteq Q</math> --- множество [[аключительное состояние автомата|''заключительных состояний'']]. | ||
'''Конечный автомат''' <math>M</math> называется ''детерминированным'', | '''Конечный автомат''' <math>M</math> называется [[Детерминированный конечный автомат|''детерминированным'']], | ||
если множество <math>\delta(q,a)</math> содержит не более одного | если множество <math>\delta(q,a)</math> содержит не более одного | ||
состояния для любых <math>q\in Q</math> и <math>a\in\Sigma</math>. Если | состояния для любых <math>q\in Q</math> и <math>a\in\Sigma</math>. Если | ||
<math>\delta(q,a)</math> всегда содержит точно одно состояние, то | <math>\delta(q,a)</math> всегда содержит точно одно состояние, то | ||
автомат <math>M</math> называется ''полностью определенным''. | автомат <math>M</math> называется [[Полностью определенный конечный автомат|''полностью определенным'']]. | ||
Любая пара <math>(q,\omega)\in Q\times\Sigma^*</math> | Любая пара <math>(q,\omega)\in Q\times\Sigma^*</math> | ||
[[Конфигурация конечного автомата|''конфигурацией'']] автомата <math>M</math>. Конфигурация | |||
<math>(q_0,\omega)</math> называется ''начальной'', а пара <math>(q,e)</math>, | <math>(q_0,\omega)</math> называется [[Начальная конфигурация конечного автомата|''начальной'']], а пара <math>(q,e)</math>, | ||
где <math>q\in F</math>, называется ''заключительной'' (или ''допускающей''). | где <math>q\in F</math>, называется [[Заключительная конфигурация конечного автомата|''заключительной'']] (или [[Допускающая конфигурация конечного автомата|''допускающей'']]). | ||
Tакт работы автомата <math>M</math> представляется бинарным отношением | Tакт работы автомата <math>M</math> представляется бинарным отношением | ||
| Строка 63: | Строка 63: | ||
Часто бывает удобно использовать графическое представление | Часто бывает удобно использовать графическое представление | ||
'''конечного автомата''' в виде так называемой ''диаграммы'' | '''конечного автомата''' в виде так называемой [[Диаграмма конечного автомата|''диаграммы'']] | ||
(или ''графа переходов'') автомата --- | (или [[Граф переходов автомата|''графа переходов'']]) автомата --- | ||
[[орграф|''орграфа'']], [[вершина|''вершины'']] которого помечены | [[орграф|''орграфа'']], [[вершина|''вершины'']] которого помечены | ||
символами состояний и в котором есть дуга <math>(p,q)</math>, если | символами состояний и в котором есть дуга <math>(p,q)</math>, если | ||
Версия от 02:06, 5 мая 2009
Конечный автомат (Finite-state automation)--- распознаватель, используемый для задания регулярных множеств. Конечный автомат состоит из входной ленты, входной головки и управляющего устройства. Входная лента --- это линейная последовательность клеток, или ячеек, каждая из которых может содержать любой символ из [math]\displaystyle{ \Sigma }[/math]. В каждый данный момент входная головка читает, или, как иногда говорят, обозревает одну входную ячейку, а управляющее устройство находится в одном состоянии из конечного множества Q, т.е. имеет конечную память.
Работа конечного автомата представляет собой некоторую последовательность шагов (или тактов). Каждый такт определяется текущим состоянием управляющего устройства и входным символом, обозреваемым в данный момент входной головкой. Сам шаг состоит из изменения состояния управляющего устройства и сдвига входной головки на одну ячейку вправо. Для каждой текущей конфигурации в общем случае существует конечное множество возможных следующих шагов, любой из которых конечный автомат может сделать, исходя из этой конфигурации.
Недетерминированный конечный автомат (или просто конечный автомат) --- это пятерка [math]\displaystyle{ M=(Q,\Sigma,\delta,q_0,F) }[/math], в которой
(1) [math]\displaystyle{ Q }[/math] --- конечное множество состояний;
(2) [math]\displaystyle{ \Sigma }[/math] --- конечное множество допустимых входных символов;
(3) [math]\displaystyle{ \delta }[/math] --- отображение множества [math]\displaystyle{ Q\times\Sigma }[/math] в множество подмножеств [math]\displaystyle{ Q }[/math], называемое функцией переходов;
(4) [math]\displaystyle{ q_0\in Q }[/math] --- выделенное начальное состояние;
(5) [math]\displaystyle{ F\subseteq Q }[/math] --- множество заключительных состояний.
Конечный автомат [math]\displaystyle{ M }[/math] называется детерминированным, если множество [math]\displaystyle{ \delta(q,a) }[/math] содержит не более одного состояния для любых [math]\displaystyle{ q\in Q }[/math] и [math]\displaystyle{ a\in\Sigma }[/math]. Если [math]\displaystyle{ \delta(q,a) }[/math] всегда содержит точно одно состояние, то автомат [math]\displaystyle{ M }[/math] называется полностью определенным.
Любая пара [math]\displaystyle{ (q,\omega)\in Q\times\Sigma^* }[/math] конфигурацией автомата [math]\displaystyle{ M }[/math]. Конфигурация [math]\displaystyle{ (q_0,\omega) }[/math] называется начальной, а пара [math]\displaystyle{ (q,e) }[/math], где [math]\displaystyle{ q\in F }[/math], называется заключительной (или допускающей).
Tакт работы автомата [math]\displaystyle{ M }[/math] представляется бинарным отношением [math]\displaystyle{ \vdash_M }[/math], определенным на конфигурациях. Если [math]\displaystyle{ \delta(q,a) }[/math] содержит [math]\displaystyle{ p }[/math], то [math]\displaystyle{ (q,a\omega)\vdash_M(p,\omega) }[/math] для всех [math]\displaystyle{ \omega\in\Sigma^* }[/math]. Отношения [math]\displaystyle{ \vdash_{M}^{+} }[/math] и [math]\displaystyle{ \vdash_{M}^{*} }[/math] являются соответственно транзитивным замыканием и рефлексивным и транзитивным замыканием отношения [math]\displaystyle{ \vdash_M }[/math].
Автомат [math]\displaystyle{ M }[/math] допускает цепочку [math]\displaystyle{ \omega\in\Sigma^* }[/math], если [math]\displaystyle{ (q_0,\omega)\vdash_{M}^{*}(q,e) }[/math] для некоторого [math]\displaystyle{ q\in F }[/math]. Языком, определяемым (распознаваемым, допускаемым) автоматом [math]\displaystyle{ M }[/math] (обозначается [math]\displaystyle{ L(M) }[/math]), называется множество входных цепочек, допускаемых автоматом [math]\displaystyle{ M }[/math], т.е. [math]\displaystyle{ L(M)=\{\omega:\omega\in\Sigma^* }[/math] и [math]\displaystyle{ (q_0,\omega)\vdash_{M}^{*}(q,e) }[/math] для некоторого [math]\displaystyle{ q\in F\} }[/math].
Часто бывает удобно использовать графическое представление
конечного автомата в виде так называемой диаграммы
(или графа переходов) автомата ---
орграфа, вершины которого помечены
символами состояний и в котором есть дуга [math]\displaystyle{ (p,q) }[/math], если
существует такой символ [math]\displaystyle{ a\in\Sigma }[/math], что [math]\displaystyle{ q\in\delta(p,a) }[/math].
Кроме того, дуга [math]\displaystyle{ (p,q) }[/math] помечается списком, состоящим из
таких [math]\displaystyle{ a }[/math], что [math]\displaystyle{ q\in\delta(p,a) }[/math].
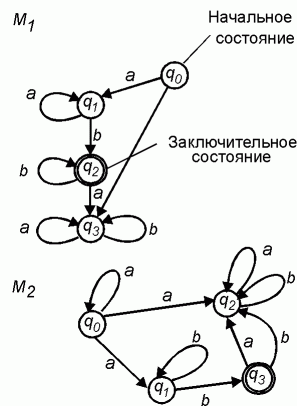
На рисунке приведены два конечных автомата, допускающих язык [math]\displaystyle{ \{a^n b^m: n\gt 0, m\gt 0\} }[/math]: [math]\displaystyle{ M_1 }[/math] --- недетерминированный, [math]\displaystyle{ M_2 }[/math] --- детерминированный полностью определенный.
См. также
Литература
[Ахо-Ульман],
[Касьянов/95],
[Касьянов-Поттосин]