Код Гапта для 2-3-деревьев: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''Код Гапта для 2-3-деревьев''' (''Gupta scheme'') - Последовательность чисел <math>a_1,a_2,\l...) |
KVN (обсуждение | вклад) Нет описания правки |
||
| (не показаны 4 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
'''Код Гапта для 2-3-деревьев''' (''Gupta scheme'') | '''Код Гапта для 2-3-деревьев''' (''[[Gupta scheme]]'') — Последовательность чисел | ||
Последовательность чисел | <math>a_1,a_2,\ldots,a_k</math> называется '''кодом Гапта''' [[2-3-Дерево|2-3-дерева]] <math>\,T</math> с [[внутренняя вершина|внутренними вершинами]] (ключами), если ее можно получить при [[обход графа|обходе]] внутренних вершин [[дерево|дерева]] <math>\,T</math> по [[уровень вершины|уровням]] снизу вверх, начиная с самого нижнего и кончая [[корень|корнем]], путем выписывания количества [[сын|сыновей]] вершин, составляющих каждый уровень, в порядке их расположения слева направо. | ||
<math>a_1,a_2,\ldots,a_k</math> называется ''' | |||
<math>T</math> с внутренними вершинами (ключами), если ее можно | [[Файл:Gupta scheme.png|700px]] | ||
получить при обходе внутренних вершин дерева <math>T</math> по уровням | |||
снизу вверх, начиная с самого нижнего и кончая корнем, путем | |||
выписывания количества сыновей вершин, составляющих каждый | |||
уровень, в порядке их расположения слева направо. | |||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
[[Категория: Коды деревьев]] | |||
Текущая версия от 08:12, 9 октября 2019
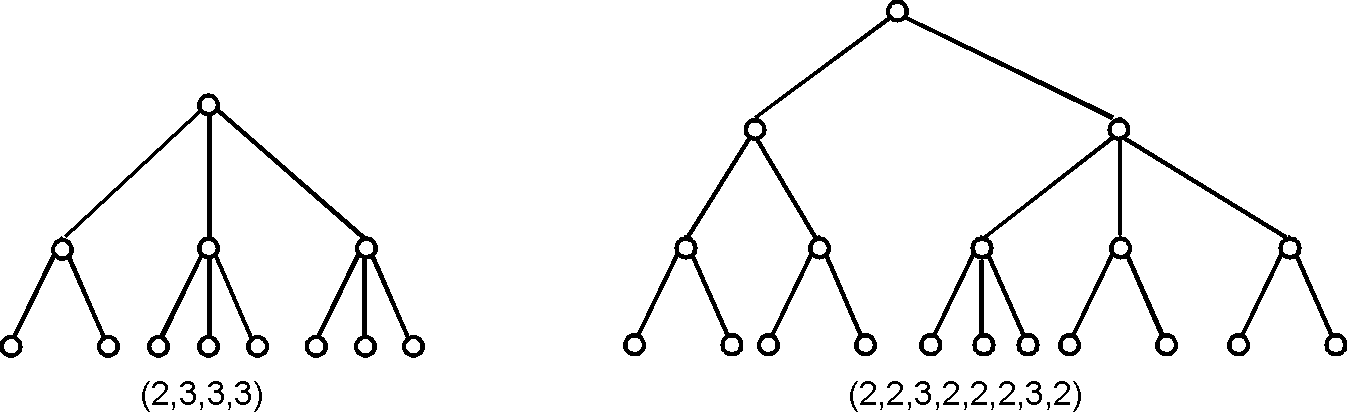
Код Гапта для 2-3-деревьев (Gupta scheme) — Последовательность чисел [math]\displaystyle{ a_1,a_2,\ldots,a_k }[/math] называется кодом Гапта 2-3-дерева [math]\displaystyle{ \,T }[/math] с внутренними вершинами (ключами), если ее можно получить при обходе внутренних вершин дерева [math]\displaystyle{ \,T }[/math] по уровням снизу вверх, начиная с самого нижнего и кончая корнем, путем выписывания количества сыновей вершин, составляющих каждый уровень, в порядке их расположения слева направо.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.