Фактор-уграф: различия между версиями
Перейти к навигации
Перейти к поиску
KEV (обсуждение | вклад) Нет описания правки |
KVN (обсуждение | вклад) Нет описания правки |
||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 1: | Строка 1: | ||
'''Фактор-уграф''' (''[[Factor-control-flow-graph]]'') | '''Фактор-уграф''' (''[[Factor-control-flow-graph]]'') — | ||
''[[уграф]]'' <math>G'</math>, который получается из исходного уграфа <math>G</math> | ''[[уграф]]'' <math>G'</math>, который получается из исходного уграфа <math>G</math> | ||
стягиванием некоторого непустого множества попарно | стягиванием некоторого непустого множества попарно | ||
| Строка 11: | Строка 11: | ||
==См. также== | ==См. также== | ||
''[[Гамачное представление]], [[Зонно-интервальное представление]], [[Иерархия вложенных альтов]], [[Иерархия вложенных зон]].'' | * ''[[Гамачное представление]],'' | ||
* ''[[Зонно-интервальное представление]],'' | |||
* ''[[Иерархия вложенных альтов]],'' | |||
* ''[[Иерархия вложенных зон]].'' | |||
==Литература== | ==Литература== | ||
[ | * Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | ||
[[Категория: Сводимые и регуляризуемые графы]] | |||
Текущая версия от 14:26, 8 октября 2019
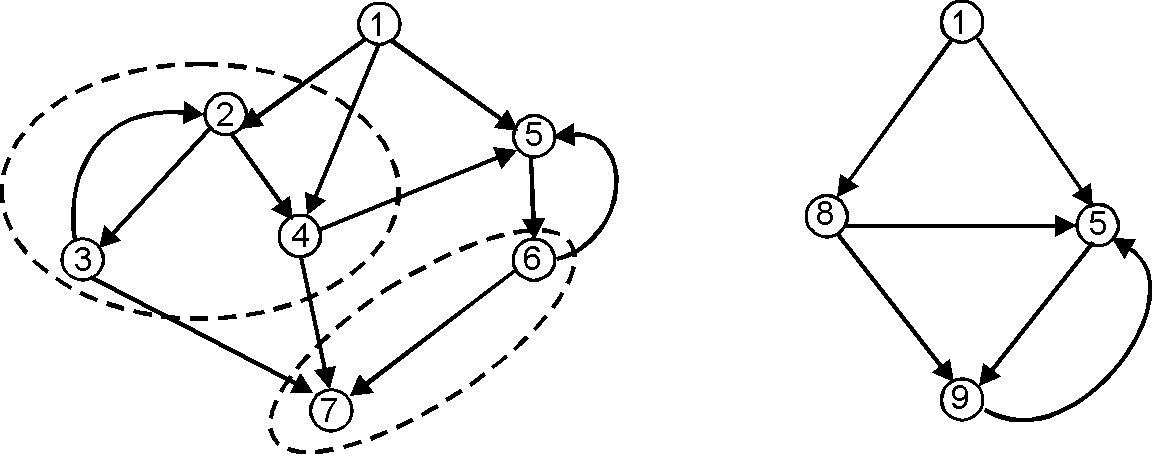
Фактор-уграф (Factor-control-flow-graph) — уграф [math]\displaystyle{ G' }[/math], который получается из исходного уграфа [math]\displaystyle{ G }[/math] стягиванием некоторого непустого множества попарно непересекающихся альтов [math]\displaystyle{ R }[/math] в вершины (обозначается [math]\displaystyle{ G'=R(G) }[/math]). Начальной (соответственно конечной) вершиной уграфа [math]\displaystyle{ G' }[/math] является либо начальная (соответственно конечная) вершина уграфа [math]\displaystyle{ G }[/math], либо тот альт из [math]\displaystyle{ R }[/math], который содержит начальную (соответственно) конечную вершину исходного уграфа.
См. также
- Гамачное представление,
- Зонно-интервальное представление,
- Иерархия вложенных альтов,
- Иерархия вложенных зон.
Литература
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.