Запрещенный подграф: различия между версиями
Перейти к навигации
Перейти к поиску
KVN (обсуждение | вклад) Нет описания правки |
KVN (обсуждение | вклад) |
||
| Строка 7: | Строка 7: | ||
* ''[[Аранжируемый граф]],'' | * ''[[Аранжируемый граф]],'' | ||
* ''[[Одновходовый граф]],'' | * ''[[Одновходовый граф]],'' | ||
* ''[[Каркас уграфа]],'' | |||
* ''[[Разборный граф]],'' | * ''[[Разборный граф]],'' | ||
* ''[[Сводимый управляющий граф]].'' | * ''[[Сводимый управляющий граф]].'' | ||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | * Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | ||
Текущая версия от 04:54, 4 сентября 2019
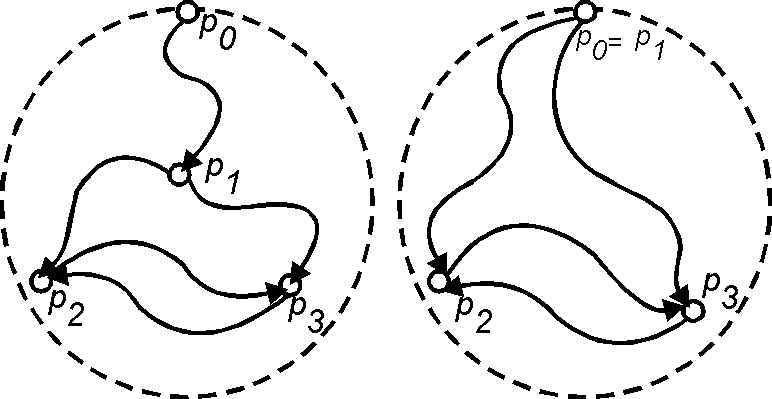
Запрещенный подграф (Forbidden subgraph) — Говорят, что уграф содержит запрещенный подграф, если в нем существуют различные вершины [math]\displaystyle{ p_1 }[/math], [math]\displaystyle{ p_2 }[/math] и [math]\displaystyle{ p_3 }[/math], что найдутся непересекающиеся по внутренним вершинам простые пути [math]\displaystyle{ P_{0,1} }[/math], [math]\displaystyle{ P_{1,2} }[/math], [math]\displaystyle{ P_{1,3} }[/math], [math]\displaystyle{ P_{2,3} }[/math], [math]\displaystyle{ P_{3,2} }[/math], где [math]\displaystyle{ P_{i,j} }[/math] обозначает путь от вершины [math]\displaystyle{ p_i }[/math] до [math]\displaystyle{ p_j }[/math]. Отсутствие в уграфе запрещенного подграфа равносильно регуляризуемости уграфа.
См. также
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.
- Касьянов В.Н., Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение. — СПб.: БХВ-Петербург, 2003.