Последовательное сравнение нескольких строк: различия между версиями
Irina (обсуждение | вклад) |
Irina (обсуждение | вклад) |
||
| Строка 9: | Строка 9: | ||
== Основные результаты == | == Основные результаты == | ||
Первое решение задачи сравнения нескольких строк заключается в применении алгоритма точного сравнения строк для локализации каждого шаблона в P. Сложность этого алгоритма составляет O(kn) в наихудшем случае. Существуют более эффективные решения, основанные на двух подходах. Первый подход, предложенный Ахо и Корасик [ ], представляет собой расширение алгоритма сравнения с одним шаблоном с помощью конечного автомата. Второй подход, реализованный Комменц-Уолтер [ ], расширяет алгоритм Бойера-Мура на случай нескольких шаблонов. | Первое решение задачи сравнения нескольких строк заключается в применении алгоритма точного сравнения строк для локализации каждого шаблона в <math>\mathcal{P}</math>. Сложность этого алгоритма составляет O(kn) в наихудшем случае. Существуют более эффективные решения, основанные на двух подходах. Первый подход, предложенный Ахо и Корасик [ ], представляет собой расширение алгоритма сравнения с одним шаблоном с помощью конечного автомата. Второй подход, реализованный Комменц-Уолтер [ ], расширяет алгоритм Бойера-Мура на случай нескольких шаблонов. | ||
Алгоритм Ахо-Корасик вначале строит бор T(P) – цифровое дерево, распознающее шаблоны P. Бор T(P) представляет собой дерево, ребра которого помечены буквами, а вдоль ветвей можно прочесть шаблоны P. Вершина p бора T(P) ассоциируется с уникальным словом w, «написанным» по пути в T(P), ведущему из его корня в p. Сам корень идентифицируется с пустым словом ". Заметим, что если w является вершиной в T(P), то w является префиксом некоторого шаблона Pi 2 P. Если вдобавок к этому 2 £, то child(w, a) совпадает с wa, если wa является вершиной в T(P), и равно NIL в противном случае. | Алгоритм Ахо-Корасик вначале строит бор <math>T(\mathcal{P})</math> – цифровое дерево, распознающее шаблоны <math>\mathcal{P}</math>. Бор <math>T(\mathcal{P})</math> представляет собой дерево, ребра которого помечены буквами, а вдоль ветвей можно прочесть шаблоны <math>\mathcal{P}</math>. Вершина p бора <math>T(\mathcal{P})</math> ассоциируется с уникальным словом w, «написанным» по пути в <math>T(\mathcal{P})</math>, ведущему из его корня в p. Сам корень идентифицируется с пустым словом ". Заметим, что если w является вершиной в <math>T(\mathcal{P})</math>, то w является префиксом некоторого шаблона Pi 2 P. Если вдобавок к этому 2 £, то child(w, a) совпадает с wa, если wa является вершиной в <math>T(\mathcal{P})</math>, и равно NIL в противном случае. | ||
На втором этапе, когда шаблоны добавляются к бору, алгоритм инициализирует выходную функцию out. Он ассоциирует одноэлементное множество {Pi} с вершинами Pi (1 < i < k) и пустое множество – со всеми другими вершинами T(P). | На втором этапе, когда шаблоны добавляются к бору, алгоритм инициализирует выходную функцию out. Он ассоциирует одноэлементное множество {Pi} с вершинами Pi (1 < i < k) и пустое множество – со всеми другими вершинами <math>T(\mathcal{P})</math>. | ||
Наконец, последним этапом предварительной обработки является создание ссылок для случаев несовпадения для каждой вершины и одновременное завершение создания выходной функции. Функция несовпадения fail определяется на вершинах следующим образом (w является вершиной): fail(w) = u, где u – самый длинный подходящий суффикс w, принадлежащий к T(P). Вычисление ссылок для несовпадений выполняется в процессе обхода T(P) в ширину. Завершение выходной функции выполняется в ходе вычисления функции для несовпадения с использованием следующего правила: если fail(w) = u, то out(w) = out(w) [ out(u). | Наконец, последним этапом предварительной обработки является создание ссылок для случаев несовпадения для каждой вершины и одновременное завершение создания выходной функции. Функция несовпадения fail определяется на вершинах следующим образом (w является вершиной): fail(w) = u, где u – самый длинный подходящий суффикс w, принадлежащий к <math>T(\mathcal{P})</math>. Вычисление ссылок для несовпадений выполняется в процессе обхода <math>T(\mathcal{P})</math> в ширину. Завершение выходной функции выполняется в ходе вычисления функции для несовпадения с использованием следующего правила: если fail(w) = u, то out(w) = out(w) [ out(u). | ||
| Строка 29: | Строка 29: | ||
После завершения этапа предварительной обработки алгоритм переходит к этапу поиска, заключающемуся в разборе текста T при помощи T(P). Он начинается с корня T(P) и использует ссылки с несовпадениями в случаях, когда символ в T не совпадает ни с одной из меток исходящих ребер текущей вершины. Каждый раз, когда встречается вершина с непустым выходным значением, это значит, что в тексте были обнаружены шаблоны выходного текста, заканчивающиеся в текущей позиции. Эта позиция является выходной. | После завершения этапа предварительной обработки алгоритм переходит к этапу поиска, заключающемуся в разборе текста T при помощи <math>T(\mathcal{P})</math>. Он начинается с корня <math>T(\mathcal{P})</math> и использует ссылки с несовпадениями в случаях, когда символ в T не совпадает ни с одной из меток исходящих ребер текущей вершины. Каждый раз, когда встречается вершина с непустым выходным значением, это значит, что в тексте были обнаружены шаблоны выходного текста, заканчивающиеся в текущей позиции. Эта позиция является выходной. | ||
Теорема 1 (Ахо и Корасик [ ]). После предварительной обработки P, поиск вхождений строк из P в тексте T может быть выполнен за время O(n x log cr). Время выполнения соответствующего этапа предварительной обработки составляет O(|P| x log cr). Обе операции требуют дополнительной памяти в объеме O(|P|). | Теорема 1 (Ахо и Корасик [ ]). После предварительной обработки <math>\mathcal{P}</math>, поиск вхождений строк из <math>\mathcal{P}</math> в тексте T может быть выполнен за время O(n x log cr). Время выполнения соответствующего этапа предварительной обработки составляет O(|P| x log cr). Обе операции требуют дополнительной памяти в объеме O(|P|). | ||
| Строка 38: | Строка 38: | ||
Комменц-Уолтер [ ] обобщила алгоритм точного сравнения строк Бойера-Мура для случая нескольких строк. Ее алгоритм строит бор для обращенных шаблонов в P вместе с двумя таблицами сдвига и применяет стратегию сканирования справа налево. Однако он довольно сложен в реализации и имеет квадратичную временную сложность в наихудшем случае. | Комменц-Уолтер [ ] обобщила алгоритм точного сравнения строк Бойера-Мура для случая нескольких строк. Ее алгоритм строит бор для обращенных шаблонов в <math>\mathcal{P}</math> вместе с двумя таблицами сдвига и применяет стратегию сканирования справа налево. Однако он довольно сложен в реализации и имеет квадратичную временную сложность в наихудшем случае. | ||
Алгоритм сравнения с помощью ОАГС (DAWG) является обобщением алгоритма BDM для точного сравнения строк. Он включает построение точной индексной структуры для обращенных строк P, такой как фактор-автомат или обобщенное суффиксное дерево, вместо протого бора, как в предыдущем варианте (см. рис. 2). Алгоритм в целом может быть сделан оптимальным за счет использования как индексной структуры для обращенных шаблонов, так и конечного автомата Ахо-Корасик для шаблонов. Поиск в этом случае включает сканирование некоторых фрагментов текста слева направо, а некоторых – справа налево. Это позволяет пропускать большие фрагменты текста T. | Алгоритм сравнения с помощью ОАГС (DAWG) является обобщением алгоритма BDM для точного сравнения строк. Он включает построение точной индексной структуры для обращенных строк <math>\mathcal{P}</math>, такой как фактор-автомат или обобщенное суффиксное дерево, вместо протого бора, как в предыдущем варианте (см. рис. 2). Алгоритм в целом может быть сделан оптимальным за счет использования как индексной структуры для обращенных шаблонов, так и конечного автомата Ахо-Корасик для шаблонов. Поиск в этом случае включает сканирование некоторых фрагментов текста слева направо, а некоторых – справа налево. Это позволяет пропускать большие фрагменты текста T. | ||
| Строка 49: | Строка 49: | ||
Теорема 2 (Крочмор и др., [ ]). Алгоритм сравнения с помощью ОАГС выполняет не более 2n сравнений символов. Предполагая, что сумма длин шаблонов в P меньше lmink, алгоритм сравнения с помощью ОАГС производит в среднем O((n\oglmin)/lmin) проверок символов текста. | Теорема 2 (Крочмор и др., [ ]). Алгоритм сравнения с помощью ОАГС выполняет не более 2n сравнений символов. Предполагая, что сумма длин шаблонов в <math>\mathcal{P}</math> меньше lmink, алгоритм сравнения с помощью ОАГС производит в среднем O((n\oglmin)/lmin) проверок символов текста. | ||
| Строка 55: | Строка 55: | ||
Техника битового параллелизма может применяться для моделирования ОАГС-алгоритма. В результате получается алгоритм Наварро и Раффино MultiBNDM [ ]. Эта стратегия эффективно работает в случае, когда /ex imin бит помещаются в нескольких машинных словах. Префиксы строк P длины Imin упаковываются в один битовый вектор. После этого поиск выполняется так же, как в алгоритме точного сравнения строк BNDM, и осуществляется для всех префиксов в одно и то же время. | Техника битового параллелизма может применяться для моделирования ОАГС-алгоритма. В результате получается алгоритм Наварро и Раффино MultiBNDM [ ]. Эта стратегия эффективно работает в случае, когда /ex imin бит помещаются в нескольких машинных словах. Префиксы строк <math>\mathcal{P}</math> длины Imin упаковываются в один битовый вектор. После этого поиск выполняется так же, как в алгоритме точного сравнения строк BNDM, и осуществляется для всех префиксов в одно и то же время. | ||
Обобщение подхода со сдвигом плохого символа, как в алгоритме точного сравнения строк Хорспула, оказывается неэффективным для задачи MSM из-за высокой вероятности нахождения каждого символа алфавита в одной из строк P. | Обобщение подхода со сдвигом плохого символа, как в алгоритме точного сравнения строк Хорспула, оказывается неэффективным для задачи MSM из-за высокой вероятности нахождения каждого символа алфавита в одной из строк <math>\mathcal{P}</math>. | ||
Алгоритм Ву и Манбера [ ] рассматривает блоки длины i. Блоки такой длинны хэшируются при помощи функции h в значения меньше maxvalue. Функция сдвига shift[h(B)] определяется как минимальное | Алгоритм Ву и Манбера [ ] рассматривает блоки длины i. Блоки такой длинны хэшируются при помощи функции h в значения меньше maxvalue. Функция сдвига shift[h(B)] определяется как минимальное значение из \P'\— j и imin - I + 1 с B = p'_l+1 : : : pij для 1 < i < k и 1 < j < jPi j. Значение I варьируется в зависимости от минимальной длины строк в <math>\mathcal{P}</math> и размера алфавита. Значение maxvalue варьируется в зависимости от объема доступной памяти. | ||
Версия от 07:11, 6 мая 2019
Ключевые слова и синонимы
Сравнение со словарем
Постановка задачи
Пусть даны конечное множество строк шаблона [math]\displaystyle{ \mathcal{P} = \{P^1, P^2, ..., Pk \} }[/math] и текстовая строка [math]\displaystyle{ T = t_1 t_2 ... t_n }[/math], где [math]\displaystyle{ T }[/math] и [math]\displaystyle{ P^i }[/math] представляют собой последовательности над алфавитом [math]\displaystyle{ \Sigma }[/math] размера [math]\displaystyle{ \sigma }[/math]. Задача сравнения нескольких строк (multiple string matching, MSM) заключается в нахождении одной или, в общем случае, всех текстовых позиций, начиная с которых [math]\displaystyle{ P^i }[/math] входит в [math]\displaystyle{ T }[/math]; или, говоря более точно, в вычислении множества [math]\displaystyle{ \{ j | \exists i, P^i = t_j t_{j + 1} ... t_{j + |P^i| - 1} \} }[/math], или эквивалентного множества [math]\displaystyle{ \{ j | \exists i, P^i = t_{j - |P^i| + 1} t_{j - |P^i| + 2} ... t_j \} }[/math]. Отметим, что в случае выдачи всех вхождений шаблонов размер выходных данных может стать квадратичным (например, в случае, когда [math]\displaystyle{ P^i }[/math] и [math]\displaystyle{ T }[/math] берутся из однобуквенного алфавита). Обозначим длину самого короткого шаблона в [math]\displaystyle{ \mathcal{P} }[/math] за [math]\displaystyle{ \ell min }[/math]. Предполагается, что шаблоны задаются в самом начале, после чего производится поиск их вхождения в нескольких текстах. Данная задача является расширением задачи точного сравнения строк.
Рассматриваются сложность в наихудшем и в среднем случаях. Во втором варианте предполагается, что шаблон и текст генерируются случайным образом посредством равномерного и независимого выбора из [math]\displaystyle{ \Sigma }[/math]. Для простоты и практичности будем далее полагать [math]\displaystyle{ |P^i| = o(n), 1 \le i \le k }[/math].
Основные результаты
Первое решение задачи сравнения нескольких строк заключается в применении алгоритма точного сравнения строк для локализации каждого шаблона в [math]\displaystyle{ \mathcal{P} }[/math]. Сложность этого алгоритма составляет O(kn) в наихудшем случае. Существуют более эффективные решения, основанные на двух подходах. Первый подход, предложенный Ахо и Корасик [ ], представляет собой расширение алгоритма сравнения с одним шаблоном с помощью конечного автомата. Второй подход, реализованный Комменц-Уолтер [ ], расширяет алгоритм Бойера-Мура на случай нескольких шаблонов.
Алгоритм Ахо-Корасик вначале строит бор [math]\displaystyle{ T(\mathcal{P}) }[/math] – цифровое дерево, распознающее шаблоны [math]\displaystyle{ \mathcal{P} }[/math]. Бор [math]\displaystyle{ T(\mathcal{P}) }[/math] представляет собой дерево, ребра которого помечены буквами, а вдоль ветвей можно прочесть шаблоны [math]\displaystyle{ \mathcal{P} }[/math]. Вершина p бора [math]\displaystyle{ T(\mathcal{P}) }[/math] ассоциируется с уникальным словом w, «написанным» по пути в [math]\displaystyle{ T(\mathcal{P}) }[/math], ведущему из его корня в p. Сам корень идентифицируется с пустым словом ". Заметим, что если w является вершиной в [math]\displaystyle{ T(\mathcal{P}) }[/math], то w является префиксом некоторого шаблона Pi 2 P. Если вдобавок к этому 2 £, то child(w, a) совпадает с wa, если wa является вершиной в [math]\displaystyle{ T(\mathcal{P}) }[/math], и равно NIL в противном случае.
На втором этапе, когда шаблоны добавляются к бору, алгоритм инициализирует выходную функцию out. Он ассоциирует одноэлементное множество {Pi} с вершинами Pi (1 < i < k) и пустое множество – со всеми другими вершинами [math]\displaystyle{ T(\mathcal{P}) }[/math].
Наконец, последним этапом предварительной обработки является создание ссылок для случаев несовпадения для каждой вершины и одновременное завершение создания выходной функции. Функция несовпадения fail определяется на вершинах следующим образом (w является вершиной): fail(w) = u, где u – самый длинный подходящий суффикс w, принадлежащий к [math]\displaystyle{ T(\mathcal{P}) }[/math]. Вычисление ссылок для несовпадений выполняется в процессе обхода [math]\displaystyle{ T(\mathcal{P}) }[/math] в ширину. Завершение выходной функции выполняется в ходе вычисления функции для несовпадения с использованием следующего правила: если fail(w) = u, то out(w) = out(w) [ out(u).
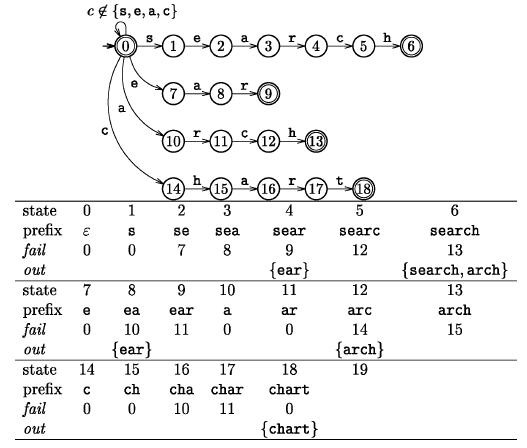
Чтобы избежать возвратов по ссылкам для несовпадений при вычислении этих ссылок, а также для обхода символов текста, для которых не был определен переход от корны на этапе поиска, к корню бора добавляется цикл для этих символов. В результате получаем механизм поиска совпадений с шаблонами или конечный автомат Ахо-Корасик (см. рис. 1).
Рисунок 1. Механизм поиска совпадений с шаблонами или конечный автомат Ахо-Корасик для множества строк {search, ear, arch, chart}
После завершения этапа предварительной обработки алгоритм переходит к этапу поиска, заключающемуся в разборе текста T при помощи [math]\displaystyle{ T(\mathcal{P}) }[/math]. Он начинается с корня [math]\displaystyle{ T(\mathcal{P}) }[/math] и использует ссылки с несовпадениями в случаях, когда символ в T не совпадает ни с одной из меток исходящих ребер текущей вершины. Каждый раз, когда встречается вершина с непустым выходным значением, это значит, что в тексте были обнаружены шаблоны выходного текста, заканчивающиеся в текущей позиции. Эта позиция является выходной.
Теорема 1 (Ахо и Корасик [ ]). После предварительной обработки [math]\displaystyle{ \mathcal{P} }[/math], поиск вхождений строк из [math]\displaystyle{ \mathcal{P} }[/math] в тексте T может быть выполнен за время O(n x log cr). Время выполнения соответствующего этапа предварительной обработки составляет O(|P| x log cr). Обе операции требуют дополнительной памяти в объеме O(|P|).
Алгоритм Ахо-Корасик, в сущности, представляет собой расширение алгоритма Морриса-Пратта для точного сравнения конечного множества строк.
Комменц-Уолтер [ ] обобщила алгоритм точного сравнения строк Бойера-Мура для случая нескольких строк. Ее алгоритм строит бор для обращенных шаблонов в [math]\displaystyle{ \mathcal{P} }[/math] вместе с двумя таблицами сдвига и применяет стратегию сканирования справа налево. Однако он довольно сложен в реализации и имеет квадратичную временную сложность в наихудшем случае.
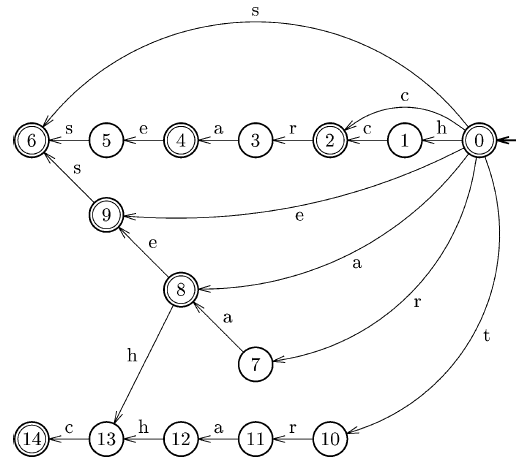
Алгоритм сравнения с помощью ОАГС (DAWG) является обобщением алгоритма BDM для точного сравнения строк. Он включает построение точной индексной структуры для обращенных строк [math]\displaystyle{ \mathcal{P} }[/math], такой как фактор-автомат или обобщенное суффиксное дерево, вместо протого бора, как в предыдущем варианте (см. рис. 2). Алгоритм в целом может быть сделан оптимальным за счет использования как индексной структуры для обращенных шаблонов, так и конечного автомата Ахо-Корасик для шаблонов. Поиск в этом случае включает сканирование некоторых фрагментов текста слева направо, а некоторых – справа налево. Это позволяет пропускать большие фрагменты текста T.
Рисунок 2. Пример ОАГС, индексной структуры, используемой для сравнения множества строк {search, ear, arch, chart}. Конечный автомат принимает обращенные префиксы строк
Теорема 2 (Крочмор и др., [ ]). Алгоритм сравнения с помощью ОАГС выполняет не более 2n сравнений символов. Предполагая, что сумма длин шаблонов в [math]\displaystyle{ \mathcal{P} }[/math] меньше lmink, алгоритм сравнения с помощью ОАГС производит в среднем O((n\oglmin)/lmin) проверок символов текста.
Узким местом ОАГС-алгоритма является объем времени и памяти, затрачиваемых на построение точной индексной структуры. Этого можно избежать, заменив точную индексную структуру оракулом фактора для множества строк. При использовании только оракула фактора получается алгоритм сопоставления с обращенным оракулом множества (Set Backward Oracle Matching, SBOM). Этот точный алгоритм демонстрирует почти такое же хорошее поведение, как и алгоритм сравнения с помощью ОАГС.
Техника битового параллелизма может применяться для моделирования ОАГС-алгоритма. В результате получается алгоритм Наварро и Раффино MultiBNDM [ ]. Эта стратегия эффективно работает в случае, когда /ex imin бит помещаются в нескольких машинных словах. Префиксы строк [math]\displaystyle{ \mathcal{P} }[/math] длины Imin упаковываются в один битовый вектор. После этого поиск выполняется так же, как в алгоритме точного сравнения строк BNDM, и осуществляется для всех префиксов в одно и то же время.
Обобщение подхода со сдвигом плохого символа, как в алгоритме точного сравнения строк Хорспула, оказывается неэффективным для задачи MSM из-за высокой вероятности нахождения каждого символа алфавита в одной из строк [math]\displaystyle{ \mathcal{P} }[/math].
Алгоритм Ву и Манбера [ ] рассматривает блоки длины i. Блоки такой длинны хэшируются при помощи функции h в значения меньше maxvalue. Функция сдвига shift[h(B)] определяется как минимальное значение из \P'\— j и imin - I + 1 с B = p'_l+1 : : : pij для 1 < i < k и 1 < j < jPi j. Значение I варьируется в зависимости от минимальной длины строк в [math]\displaystyle{ \mathcal{P} }[/math] и размера алфавита. Значение maxvalue варьируется в зависимости от объема доступной памяти.
На этапе поиска этого алгоритма производится чтение блоков B длины i. Если shift[h(B)] > 0, то выполняется сдвиг на длину shift[h(B)]. В противном случае при shift[h(B)] = 0 шаблоны, оканчивающиеся на блок B, проверяются в тексте один за другим. Первым сканируется блок timjn-i+i timjn. Данный метод встроен в команду agrep [10].