Геометрическая протяженность геометрических сетей

Ключевые слова и синонимы

Обход; коэффициент растяжения; показатель растяжения

Постановка задачи

Городские системы улично-дорожной сети можно моделировать плоскими геометрическими сетями G = (V, E), ребра которых [math]\displaystyle{ e \in E \; }[/math] представляют собой кусочно гладкие кривые, соединяющие вершины [math]\displaystyle{ v \in V \subset \mathbb{R}^2 \; }[/math].

Ребра не пересекаются нигде, кроме общих конечных точек в V. Поскольку вдоль улиц стоят дома, качество подобной сети может измеряться в длине путей между любыми двумя произвольными точками p и q в G.

Обозначим за [math]\displaystyle{ \xi_G (p, q) \; }[/math] кратчайший путь из p в q по G. Тогда

(1) [math]\displaystyle{ \delta(p, q) := \frac{| \xi_G (p, q) |}{|pq|} }[/math]

представляет собой обход, по которому необходимо идти при перемещении по сети G из точки p в точку q, вместо того чтобы пройти напрямую. Здесь |.| обозначает евклидову длину. Геометрическая протяженность сети G задается соотношением

(2) [math]\displaystyle{ \delta(G) := sup_{p \ne q \in G} \; \delta(p, q) }[/math].

Это определение отличается от понятия коэффициента растяжения, использовавшегося в контексте остовных деревьев; подробнее об этом – в монографиях Эпштейна [6] или Нарасимхана и Смида [11]. В последней рассматриваются только пути между вершинами [math]\displaystyle{ p, q \in V \; }[/math], тогда как понятие геометрической протяженности включает также все точки на ребрах. Таким образом, коэффициент растяжения треугольника T равен 1, однако его геометрическая протяженность задается формулой [math]\displaystyle{ \delta(T) = \sqrt{2 / (1 - cos \; \alpha)} \ge 2 }[/math], где [math]\displaystyle{ \alpha \le 60^\circ \; }[/math] - самый острый угол T.

Пусть дано конечное множество S точек на плоскости. Требуется найти конечную геометрическую сеть, содержащую S, геометрическая протяженность которой насколько возможно мала. Значение

[math]\displaystyle{ \Delta(S) := inf \{ \delta(G); G \; }[/math] – конечная плоская геометрическая сеть, содержащая [math]\displaystyle{ S \} \; }[/math]

называется геометрической протяженностью множества точек S. Задача заключается в вычислении или ограничении [math]\displaystyle{ \Delta(S) \; }[/math] для данного множества S.

Основные результаты

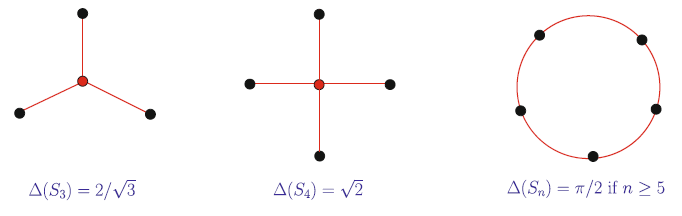
Теорема 1 [4]. Обозначим за [math]\displaystyle{ S_n \; }[/math] множество вершин правильного n-угольника. Тогда [math]\displaystyle{ \Delta(S_3) = 2 / \sqrt{3}, \Delta(S_4) = \sqrt{2}, \Delta(S_n) = \pi / 2 \; }[/math] для всех [math]\displaystyle{ n \ge 5 \; }[/math].

Сети, в которых достигаются такие минимальные значения, изображены на рис. 1. В доказательстве минимальности используются следующие две леммы, которые интересны и сами по себе. Лемма 1 была независимо получена Ароновым и др. [1].

Рисунок 1. Вложения с минимальной протяженностью для регулярных множеств точек

Лемма 1. Пусть T – дерево, содержащее [math]\displaystyle{ S_n \; }[/math]. Тогда [math]\displaystyle{ \delta(T) \ge n / \pi }[/math].

Лемма 2 следует из результата, полученного Громовым [7]. Ее проще доказать при помощи формулы Коши для расчета площади поверхности [4].

Лемма 2. Обозначим за C простую замкнутую кривую на плоскости. Тогда [math]\displaystyle{ \delta(C) \ge \pi / 2 }[/math].

Очевидно, для круга лемма 2 выполняется со знаком равенства. Из следующей леммы следует, что круг – единственная замкнутая кривая, имеющая минимальную геометрическую протяженность [math]\displaystyle{ \pi / 2 \; }[/math].

Лемма 3 [3]. Обозначим за C простую замкнутую кривую на плоскости с геометрической протяженностью, меньшей [math]\displaystyle{ \pi / 2 + \epsilon (\delta) }[/math]. В таком случае C содержится в кольце ширины [math]\displaystyle{ \delta \; }[/math].

Для точек, имеющих общее положение, вычисление геометрической протяженности оказывается весьма сложным. Решение этой задачи полностью известно только для множеств S = {A, B, C} величины 3.

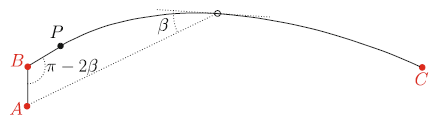
Теорема 2 [5]. Плоская геометрическая сеть с минимальной геометрической протяженностью, содержащая три заданные точки {A, B, C}, представляет собой либо отрезок прямой, либо дерево Штейнера, представленное на рис. 1, либо простой путь, состоящий из двух отрезков прямых и одного сегмента экспоненциальной спирали, см. рис. 2.

Оптимальный путь, представленный на рис. 2, содержит вершину Штейнера степени 2, P, расположенную на расстоянии |AB| от B. Путь от A к B и от B к P идет по прямой. От P к C он идет по экспоненциальной спирали с центром в A.

Рисунок 2. Вложение с минимальной протяженностью для точек A, B и C

Следующий результат задает верхнюю и нижнюю границы [math]\displaystyle{ \Delta (S) \; }[/math].

Теорема 3 [4]. Для каждого конечного множества точек S выполняется соотношение [math]\displaystyle{ \Delta(S) \lt 1,678 \; }[/math].

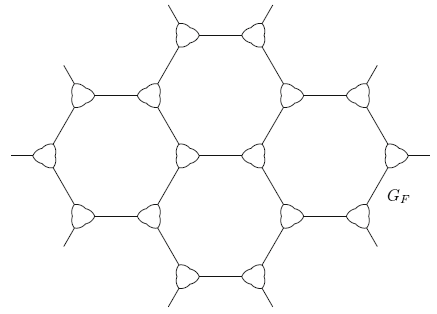
Для доказательства верхней границы заменим каждую вершину шестиугольного черепичного разбиения [math]\displaystyle{ \mathbb{R}^2 \; }[/math] определенной замкнутой кривой Зиндлера (по определению, все пары точек, делящие пополам периметр кривой Зиндлера, находятся на одинаковом расстоянии). В результате получаем сеть [math]\displaystyle{ G_F \; }[/math] с геометрической протяженностью, приблизительно равной 1,6778, см. рис. 3. Пусть дано конечное множество точек S. Применим небольшую деформацию к масштабированной версии [math]\displaystyle{ G_F \; }[/math], такую, чтобы все точки S лежали в конечной части, G, деформированного множества. Согласно теореме Дирихле о приближении действительных чисел рациональными, достаточно выполнить деформацию, малую относительно размера ячейки, так что на протяженность она не повлияет. Определение и свойства кривых Зиндлера см. в [8].

Рисунок 3. Сеть с геометрической протяженностью, приблизительно равной 1,6778

Теорема 4 [3]. Существует конечное множество точек S, такое, что [math]\displaystyle{ \Delta(S) \gt (1 + 10^{-11}) \; \pi / 2 }[/math].

Теорема 4 выполняется для множества точек S размером 19 x 19 вершин целочисленной решетки. Грубо говоря, если S заключено в геометрическую сеть G с протяженностью, близкой к [math]\displaystyle{ \pi / 2 \; }[/math], то, согласно лемме 3, границы граней G должны быть заключены в небольшом кольце. Для получения внутреннего и внешнего кругов этого кольца следует воспользоваться утверждением Купербергов и др. [9], гласящим, что расширение упаковки дисков радиуса [math]\displaystyle{ \le 1 \; }[/math] на определенный коэффициент не может покрыть квадрат со стороной 4.

Применение

Понятие геометрической протяженности применяется в теории узлов; см, например, Куснер и Салливан [10], Денн и Салливан [2]. Применительно к градостроительному проектированию вышеприведенные соображения задают основные границы протяженности при соединении заданных площадок при помощи плоских геометрических сетей.

Открытые вопросы

Для практического применения в дополнение к верхним границам геометрической протяженности пригодились бы верхние границы веса (т.е. общей длины ребер) геометрической сети. Некоторые теоретические вопросы также требуют дополнительного исследования. Всегда ли [math]\displaystyle{ \Delta(S) \; }[/math] достигается для конечной сети? Как вычислить (точно или приближенно) [math]\displaystyle{ \Delta(S) \; }[/math] для заданного конечного множества S? Чему равняется точное значение sup{[math]\displaystyle{ \Delta(S) \; }[/math]; S finite}?

См. также

• Протяженность геометрических сетей

Литература

1. Aronov, B., de Berg, M., Cheong, O., Gudmundsson, J., Haverkort, H., Vigneron, A.: Sparse Geometric Graphs with Small Dilation. 16th International Symposium ISAAC 2005, Sanya. In: Deng, X., Du, D. (eds.) Algorithms and Computation, Proceedings. LNCS, vol. 3827, pp. 50-59. Springer, Berlin (2005)

2. Denne, E., Sullivan, J.M.: The Distortion of a Knotted Curve. http://www.arxiv.org/abs/math.GT/0409438 (2004)

3. Dumitrescu, A., Ebbers-Baumann, A., GrCine, A., Klein, R., Rote, G.: On the Geometric Dilation of Closed Curves, Graphs, and Point Sets. Comput. Geom. Theory Appl. 36(1), 16-38(2006)

4. Ebbers-Baumann, A., GrCine, A., Klein, R.: On the Geometric Dilation of Finite Point Sets. Algorithmica 44(2), 137-149 (2006)

5. Ebbers-Baumann, A., Klein, R., Knauer, C., Rote, G.: The Geometric Dilation of Three Points. Manuscript (2006)

6. Eppstein, D.: Spanning Trees and Spanners. In: Sack, J.-R., Urrutia, J. (eds.) Handbook of Computational Geometry, pp. 425-461. Elsevier, Amsterdam (1999)

7. Gromov, M.: Structures Metriques desVarietes Riemanniennes. Textes Math. CEDIX, vol. 1. F. Nathan, Paris (1981)

8. GrCine, A.: Geometric Dilation and Halving Distance. Ph. D. thesis, Institut fur Informatik I, Universitat Bonn (2006)

9. Kuperberg, K., Kuperberg, W., Matousek, J., Valtr, P.: Almost Tiling the Plane with Ellipses. Discrete Comput. Geom. 22(3), 367-375(1999)

10. Kusner, R.B., Sullivan, J.M.: On Distortion and Thickness of Knots. In: Whittington, S.G. et al. (eds.) Topology and Geometry in Polymer Science. IMA Volumes in Math. and its Applications, vol. 103, pp. 67-78. Springer, New York (1998)

11. Narasimhan, G., Smid, M.: Geometric Spanner Networks. Cambridge University Press(2007)