Обобщенная двухсерверная задача: различия между версиями
Irina (обсуждение | вклад) мНет описания правки |
Irina (обсуждение | вклад) мНет описания правки |
||
| Строка 13: | Строка 13: | ||
'''Задачи онлайн-маршрутизации''' | '''Задачи онлайн-маршрутизации''' | ||
Обобщенная двухсерверная задача относится к классу задач маршрутизации под названием ''систем | Обобщенная двухсерверная задача относится к классу задач маршрутизации под названием ''метрических систем сервисов'' [5, 10]. Подобную систему определяют метрическое пространство <math>\mathbb{M} \;</math> всех возможных конфигураций системы, начальная конфигурация <math>C_0 \;</math> и множество <math>\mathcal{R} \;</math> возможных запросов, в котором каждый запрос <math>r \in \mathcal{R} \;</math> является подмножеством <math>\mathbb{M} \;</math>. Пусть дана последовательность запросов <math>r_1, r_2, ..., r_n \;</math>. Допустимым решением является последовательность конфигураций <math>C_1, C_2, ..., C_n \;</math>, такая, что <math>C_i \in r_i \;</math> для всех <math>i \in \{ 1, ..., n \} \;</math>. | ||
При моделировании обобщенной двухсерверной задачи системой | При моделировании обобщенной двухсерверной задачи метрической системой сервисов мы получаем <math>\mathbb{M} = \mathbb{X} \times \mathbb{Y}</math> и <math>\mathcal{R} = \{ \{ x \times \mathbb{Y} \} \cup \{ \mathbb{X} \times y \} | x \in \mathbb{X}, y \in \mathbb{Y} \}</math>. В классической двухсерверной задаче оба сервера перемещаются в одном и том же пространстве и получают одни и те же запросы, т.е. <math>\mathbb{M} = \mathbb{X} \times \mathbb{X}</math> и <math>\mathcal{R} = \{ \{ x \times \mathbb{X} \} \cup \{ \mathbb{X} \times x \} | x \in \mathbb{X} \}</math>. | ||
| Строка 25: | Строка 25: | ||
== Основные результаты == | == Основные результаты == | ||
Основным результатом работы [11] является достаточное условие наличия константно-конкурентного алгоритма для системы | Основным результатом работы [11] является достаточное условие наличия константно-конкурентного алгоритма для метрической системы сервисов. Кроме того, авторы продемонстрировали, что это условие выполняется и для обобщенной двухсерверной задачи. | ||
Для фиксированной системы | Для фиксированной метрической системы сервисов S с метрическим пространством <math>\mathbb{M} \;</math> обозначим за <math>A(C, \sigma) \;</math> стоимость работы алгоритма A на входной последовательности <math>\sigma \;</math>, начинающего работу с конфигурации C. Пусть <math>OPT(C, \sigma) \;</math> – стоимость соответствующего оптимального решения. Мы говорим, что путь T в <math>\mathbb{M} \;</math> ''обслуживает'' последовательность <math>\sigma \;</math>, если он посещает все запросы по порядку. Следовательно, допустимым путем является такой путь, который обслуживает всю последовательность и начинается с исходной конфигурации. | ||
| Строка 34: | Строка 34: | ||
'''Теорема 1. Пусть S – система | '''Теорема 1. Пусть S – метрическая система сервисов с метрическим пространством <math>\mathbb{M} \;</math>. Предположим, что существует алгоритм A и константы <math>\alpha \ge 1, \beta \ge 0, m \ge 2 \;</math>, такие, что для любой точки <math>C \in \mathbb{M} \;</math>, последовательности <math>\sigma \;</math> и попарно независимых путей <math>T_1, T_2, ... , T_m \;</math>, обслуживающих <math>\sigma \;</math>, выполняется соотношение''' | ||
'''(1) <math>A(C, \sigma) \le \alpha OPT(C, \sigma) + \beta \sum^m_{i = 1} | T_i |</math>.''' | '''(1) <math>A(C, \sigma) \le \alpha OPT(C, \sigma) + \beta \sum^m_{i = 1} | T_i |</math>.''' | ||
| Строка 47: | Строка 47: | ||
== Применение == | == Применение == | ||
Множество систем | Множество метрических систем сервисов можно объединить, получив так называемую ''систему сумм'' [9]. Запрос к системе сумм включает по одному запросу к каждой системе, и для его обслуживания необходимо обслужить по меньшей мере один из отдельных запросов. Обобщенная двухсерверная задача может рассматриваться как одна из самых простых систем сумм, поскольку две отдельных задачи являются совершенно тривиальными: имеется один сервер, и каждый запрос состоит из одного пункта. | ||
Версия от 07:42, 18 декабря 2017
Ключевые слова и синонимы
CNN-задача
Постановка задачи
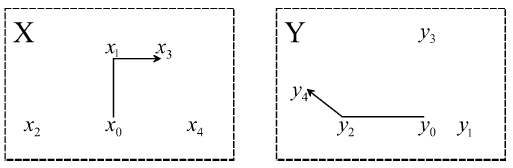
В обобщенной двухсерверной задаче имеются два сервера, один из которых перемещается в метрическом пространстве [math]\displaystyle{ \mathbb{X} \; }[/math], а другой – в метрическом пространстве [math]\displaystyle{ \mathbb{Y} \; }[/math]. Они обслуживают запросы [math]\displaystyle{ r \in \mathbb{X} \times \mathbb{Y} \; }[/math], которые поступают один за одним. Запрос r = (x, y) обслуживается посредством перемещения [math]\displaystyle{ \mathbb{X} }[/math]-сервера в точку x либо [math]\displaystyle{ \mathbb{Y} }[/math]-сервера в точку y. Решение, какой из двух серверов переместить при следующем запросе, не подлежит отмене и принимается в отсутствие каких-либо знаний о будущих запросах. Задача заключается в минимизации расстояния, пройденного обоими серверами.
Рис. 1. В этом примере оба сервера перемещаются по плоскости и начинают движение с конфигурации ([math]\displaystyle{ x_0, y_0 \; }[/math]). [math]\displaystyle{ \mathbb{X} }[/math]-сервер перемещается при выполнении запросов 1 и 3, [math]\displaystyle{ \mathbb{Y} }[/math]-сервер обслуживает запросы 2 и 4. Стоимость решения представляет собой сумму длин путей
Задачи онлайн-маршрутизации
Обобщенная двухсерверная задача относится к классу задач маршрутизации под названием метрических систем сервисов [5, 10]. Подобную систему определяют метрическое пространство [math]\displaystyle{ \mathbb{M} \; }[/math] всех возможных конфигураций системы, начальная конфигурация [math]\displaystyle{ C_0 \; }[/math] и множество [math]\displaystyle{ \mathcal{R} \; }[/math] возможных запросов, в котором каждый запрос [math]\displaystyle{ r \in \mathcal{R} \; }[/math] является подмножеством [math]\displaystyle{ \mathbb{M} \; }[/math]. Пусть дана последовательность запросов [math]\displaystyle{ r_1, r_2, ..., r_n \; }[/math]. Допустимым решением является последовательность конфигураций [math]\displaystyle{ C_1, C_2, ..., C_n \; }[/math], такая, что [math]\displaystyle{ C_i \in r_i \; }[/math] для всех [math]\displaystyle{ i \in \{ 1, ..., n \} \; }[/math].
При моделировании обобщенной двухсерверной задачи метрической системой сервисов мы получаем [math]\displaystyle{ \mathbb{M} = \mathbb{X} \times \mathbb{Y} }[/math] и [math]\displaystyle{ \mathcal{R} = \{ \{ x \times \mathbb{Y} \} \cup \{ \mathbb{X} \times y \} | x \in \mathbb{X}, y \in \mathbb{Y} \} }[/math]. В классической двухсерверной задаче оба сервера перемещаются в одном и том же пространстве и получают одни и те же запросы, т.е. [math]\displaystyle{ \mathbb{M} = \mathbb{X} \times \mathbb{X} }[/math] и [math]\displaystyle{ \mathcal{R} = \{ \{ x \times \mathbb{X} \} \cup \{ \mathbb{X} \times x \} | x \in \mathbb{X} \} }[/math].
Эффективность алгоритмов онлайн-оптимизации нередко измеряется при помощи сравнительного (конкурентного) анализа. Мы утверждаем, что алгоритм является [math]\displaystyle{ \; \alpha }[/math]-конкурентным ([math]\displaystyle{ \alpha \ge 1 \; }[/math]) для некоторой задачи минимизации, если для любого возможного экземпляра задачи стоимость решения алгоритма не более чем в [math]\displaystyle{ \alpha \; }[/math] раз превышает стоимость оптимального решения для этого экземпляра.
Стандартный алгоритм, который доказуемо эффективно справляется с несколькими элементарными задачами маршрутизации – это так называемый алгоритм рабочей функции [2, 6, 8]. После каждого запроса алгоритм перемещается в конфигурацию с низкой стоимостью, находящуюся не слишком далеко от текущей конфигурации. Точнее говоря, если после обслуживания последовательности [math]\displaystyle{ \sigma \; }[/math] система имеет конфигурацию C, а [math]\displaystyle{ r \subseteq \mathbb{M} \; }[/math] – следующий запрос, то алгоритм рабочей функции с параметром [math]\displaystyle{ \lambda \ge 1 \; }[/math] переходит к конфигурации [math]\displaystyle{ C' \in r \; }[/math], которая минимизирует соотношение [math]\displaystyle{ \lambda W_{\sigma, r} (C') + d(C, C') \; }[/math], где d(C, C') – расстояние между конфигурациями C и C', а [math]\displaystyle{ W_{\sigma, r} (C') \; }[/math] – стоимость оптимального решения, обслуживающего все запросы (по порядку) в [math]\displaystyle{ \sigma \; }[/math] плюс запрос r с тем ограничением, что оно завершает работу в конфигурации C'.
Основные результаты
Основным результатом работы [11] является достаточное условие наличия константно-конкурентного алгоритма для метрической системы сервисов. Кроме того, авторы продемонстрировали, что это условие выполняется и для обобщенной двухсерверной задачи.
Для фиксированной метрической системы сервисов S с метрическим пространством [math]\displaystyle{ \mathbb{M} \; }[/math] обозначим за [math]\displaystyle{ A(C, \sigma) \; }[/math] стоимость работы алгоритма A на входной последовательности [math]\displaystyle{ \sigma \; }[/math], начинающего работу с конфигурации C. Пусть [math]\displaystyle{ OPT(C, \sigma) \; }[/math] – стоимость соответствующего оптимального решения. Мы говорим, что путь T в [math]\displaystyle{ \mathbb{M} \; }[/math] обслуживает последовательность [math]\displaystyle{ \sigma \; }[/math], если он посещает все запросы по порядку. Следовательно, допустимым путем является такой путь, который обслуживает всю последовательность и начинается с исходной конфигурации.
Пути [math]\displaystyle{ T_1 \; }[/math] и [math]\displaystyle{ T_2 \; }[/math] называются независимыми, если они разделены следующим образом: [math]\displaystyle{ |T_1| + |T_2| \lt d(C^s_1, C^t_2) + d(C^s_2, C^t_1) \; }[/math], где [math]\displaystyle{ C_i^s \; }[/math] и [math]\displaystyle{ C_i^t \; }[/math] – начальная и конечная точки пути [math]\displaystyle{ T_i \; (i \in \{ 1, 2 \}) }[/math], соответственно. Заметим, в частности, что пересекающиеся пути не являются независимыми.
Теорема 1. Пусть S – метрическая система сервисов с метрическим пространством [math]\displaystyle{ \mathbb{M} \; }[/math]. Предположим, что существует алгоритм A и константы [math]\displaystyle{ \alpha \ge 1, \beta \ge 0, m \ge 2 \; }[/math], такие, что для любой точки [math]\displaystyle{ C \in \mathbb{M} \; }[/math], последовательности [math]\displaystyle{ \sigma \; }[/math] и попарно независимых путей [math]\displaystyle{ T_1, T_2, ... , T_m \; }[/math], обслуживающих [math]\displaystyle{ \sigma \; }[/math], выполняется соотношение
(1) [math]\displaystyle{ A(C, \sigma) \le \alpha OPT(C, \sigma) + \beta \sum^m_{i = 1} | T_i | }[/math].
Тогда существует алгоритм B, являющийся константно-конкурентным для S.
Доказательство вышеприведенной теоремы в работе [11] включает явную формулировку алгоритма B. Этот алгоритм объединяет алгоритм A с алгоритмом рабочей функции и действует поэтапно. На каждом этапе он применяет алгоритм A до тех пор, пока его стоимость не становится слишком большой по сравнению с оптимальной. Затем он выполняет один проход алгоритма рабочей функции и начинает новый этап. На каждом этапе алгоритм A выполняет перезапуск, т.е. принимает конечную конфигурацию предыдущего этапа в качестве начальной, тогда как алгоритм рабочей функции помнит всю последовательность запросов.
Для обобщенной двухсерверной задачи так называемый алгоритм баланса удовлетворяет условию (1). Этот алгоритм сохраняет кумулятивную стоимость обоих серверов и при получении каждого запроса перемещает тот сервер, при котором максимум двух новых значений будет минимальным. Сам по себе алгоритм баланса не является константно-конкурентным, однако, согласно теореме 1, если мы рационально объединим его с алгоритмом рабочей функции, мы получим константно-конкурентный алгоритм.
Применение
Множество метрических систем сервисов можно объединить, получив так называемую систему сумм [9]. Запрос к системе сумм включает по одному запросу к каждой системе, и для его обслуживания необходимо обслужить по меньшей мере один из отдельных запросов. Обобщенная двухсерверная задача может рассматриваться как одна из самых простых систем сумм, поскольку две отдельных задачи являются совершенно тривиальными: имеется один сервер, и каждый запрос состоит из одного пункта.
Системы сумм могли бы быть особенно полезными для моделирования систем хранения и извлечения информации. Для повышения стабильности или эффективности можно хранить копии одной и той же информации в нескольких системах (например, базах данных или жестких дисках). Для извлечения одного фрагмента информации мы можем прочитать его из любой системы. Однако чтение информации может сопровождаться необходимостью изменения конфигурации системы. Например, если база данных хранится в виде бинарного дерева поиска, то было бы эффективным вносить изменения в структуру дерева на ходу, то есть использовать динамические деревья поиска [12].
Открытые вопросы
Доказательство того, что алгоритм рабочей функции является конкурентным для обобщенной двухсерверной задачи (как было предположено в [9] и [11]), по-прежнему не представлено. Также неизвестен рандомизированный алгоритм с меньшим коэффициентом конкурентоспособности, чем приведен в [11]. Помимо нижней границы, не имеется других известных результатов для обобщенной задачи с более чем двумя серверами. Неизвестно даже, может ли алгоритм рабочей функции для нее быть конкурентным.
Существуют системы, для которых этот алгоритм не является конкурентным. Было бы любопытно получить нетривиальное свойство, из которого следовала бы конкурентность алгоритма рабочей функции.
См. также
- Алгоритм DC-дерева для k серверов на деревьях
- Системы метрических задач
- Подкачка и кэширование интернет-страниц
- Алгоритм рабочей функции для k серверов
Литература
1. Borodin, A., El-Yaniv, R.: Online computation and competitive analysis. Cambridge University Press, Cambridge (1998)
2. Burley, W.R.: Traversing layered graphs using the work function algorithm. J. Algorithms 20,479-511 (1996)
3. Chrobak, M.: Sigact news online algorithms column 1. ACM SIGACTNews 34,68-77 (2003)
4. Chrobak, M., Karloff, H., Payne, T.H., Vishwanathan, S.: New results on server problems. SIAM J. Discret. Math. 4, 172-181 (1991)
5. Chrobak, M., Larmore, L.L.: Metrical service systems: Deterministic strategies. Tech. Rep. UCR-CS-93-1, Department of Computer Science, Univ. of California at Riverside (1992)
6. Chrobak, M., Sgall, J.: The weighted 2-server problem. Theor. Comput. Sci. 324,289-312 (2004)
7. Fiat, A., Ricklin, M.: Competitive algorithms for the weighted server problem.Theor. Comput. Sci. 130,85-99 (1994)
8. Koutsoupias, E., Papadimitriou, C.H.: On the k-server conjecture. J.ACM 42,971-983 (1995)
9. Koutsoupias, E., Taylor, D.S.: The CNN problem and other k-server variants. Theor. Comput. Sci. 324, 347-359 (2004)
10. Manasse, M.S., McGeoch, L.A., Sleator, D.D.: Competitive algorithms for server problems. J. Algorithms 11, 208-230 (1990)
11. Sitters, R.A., Stougie, L.: The generalized two-server problem. J.ACM 53,437^58 (2006)
12. Sleator, D.D., Tarjan, R.E.: Self-adjusting binary search trees. J.ACM 32,652-686 (1985)