Задача присваивания: различия между версиями
Irina (обсуждение | вклад) |
Irina (обсуждение | вклад) |
||
| Строка 15: | Строка 15: | ||
и | и | ||
<math>\forall x \in X \; \; \; \ell(x) max_{y \in Y} \; w(x, y).</math> | <math>\forall x \in X \; \; \; \ell(x) = max_{y \in Y} \; w(x, y).</math> | ||
Определим подграф равенства, | Определим ''подграф равенства'', <math>G_{ \ell}\;</math>, как остовный подграф G, содержащий все вершины G и только те ребра (x, y), веса которых удовлетворяют условию <math>w(x, y) = \ell(x) + \ell(y) \;</math>. | ||
| Строка 24: | Строка 24: | ||
'''Теорема 1. Если подграф равенства | '''Теорема 1. Если подграф равенства, <math>G_{ \ell}\;</math>, содержит совершенное паросочетание M*, то M* является в G паросочетанием с максимальным весом.''' | ||
| Строка 32: | Строка 32: | ||
'''Высокоуровневое описание''' | '''Высокоуровневое описание''' | ||
Вышеприведенная теорема служит основой алгоритма нахождения паросочетания с максимальным весом в полном двудольном графе. Начав с допустимой разметки, вычислим подграф равенства и затем найдем максимальное паросочетание в этом подграфе (на этом этапе веса ребер не учитываются). Если найденное паросочетание является совершенным, процесс на этом завершается. В противном случае к подграфу равенства добавляются ребра посредством пересмотра меток вершин. После добавления ребер к подграфу равенства либо увеличивается размер паросочетания (был найден дополняющий путь), либо продолжает расти венгерское дерево. | Вышеприведенная теорема служит основой алгоритма нахождения паросочетания с максимальным весом в полном двудольном графе. Начав с допустимой разметки, вычислим подграф равенства и затем найдем максимальное паросочетание в этом подграфе (на этом этапе веса ребер не учитываются). Если найденное паросочетание является совершенным, процесс на этом завершается. В противном случае к подграфу равенства добавляются ребра посредством пересмотра меток вершин. После добавления ребер к подграфу равенства либо увеличивается размер паросочетания (был найден дополняющий путь), либо продолжает расти [[венгерское дерево]]. В первом случае этот этап процесса завершается и начинается новый (поскольку размер паросочетания вырос). Во втором случае венгерское дерево растет за счет добавления к нему новых вершин, что, очевидно, не может произойти более n раз. | ||
''(Структура венгерского дерева включает исследованные ребра при поиске базисного возможного решения одновременно из всех свободных вершин в S. Когда в T найдена вершина, сопоставленная какой-либо вершине из S, нужно исследовать только соответствующее ребро; однако в S исследуются все ребра, инцидентные этой вершине).'' | |||
| Строка 41: | Строка 41: | ||
Стоит отметить свойство данного алгоритма: | Стоит отметить следующее свойство данного алгоритма: | ||
S | |||
Версия от 04:42, 20 ноября 2016
Ключевые слова и синонимы
Паросочетание на взвешенных двудольных графах
Постановка задачи
Пусть дан полный двудольный граф [math]\displaystyle{ G = (X, F, X \times Y) \; }[/math] с присвоенным каждому ребру (x, y) весом w(x, y). Паросочетание M представляет собой подмножество ребер, такое, что никакие два ребра в M не имеют общей вершины. Паросочетание является совершенным, если в него входят все вершины. Предположим, что |X| = |Y| = n. Задача поиска паросочетания на взвешенных двудольных графах заключается в нахождении паросочетания с максимальным общим весом, где [math]\displaystyle{ w(M) = \sum_{e \in M} w(e) \; }[/math]. Поскольку граф G является полным и двудольным, у него имеется совершенное паросочетание. Алгоритм для решения данной задачи предложили Кун [4] и Манкрес [6]. Будем предполагать, что всех веса ребер неотрицательны.
Основные результаты
Определим допустимую разметку вершин [math]\displaystyle{ \ell \; }[/math] как отображение множества вершин G на множество вещественных чисел, где [math]\displaystyle{ \ell(x) + \ell(y) \ge w(x, y) \; }[/math].
Назовем [math]\displaystyle{ \ell(x) \; }[/math] меткой вершины x. Допустимую разметку вершин легко вычислить следующим образом:
[math]\displaystyle{ \forall y \in Y \; \; \; \ell(y) = 0 }[/math]
и
[math]\displaystyle{ \forall x \in X \; \; \; \ell(x) = max_{y \in Y} \; w(x, y). }[/math]
Определим подграф равенства, [math]\displaystyle{ G_{ \ell}\; }[/math], как остовный подграф G, содержащий все вершины G и только те ребра (x, y), веса которых удовлетворяют условию [math]\displaystyle{ w(x, y) = \ell(x) + \ell(y) \; }[/math].
Связь между подграфами равенства и паросочетаниями с максимальным весом задается следующей теоремой.
Теорема 1. Если подграф равенства, [math]\displaystyle{ G_{ \ell}\; }[/math], содержит совершенное паросочетание M*, то M* является в G паросочетанием с максимальным весом.
Заметим, что сумма меток является верхней границей веса паросочетания с максимальным весом. Алгоритм последовательно находит паросочетание и допустимую разметку, такие, что вес паросочетания оказывается равен сумме всех меток.
Высокоуровневое описание
Вышеприведенная теорема служит основой алгоритма нахождения паросочетания с максимальным весом в полном двудольном графе. Начав с допустимой разметки, вычислим подграф равенства и затем найдем максимальное паросочетание в этом подграфе (на этом этапе веса ребер не учитываются). Если найденное паросочетание является совершенным, процесс на этом завершается. В противном случае к подграфу равенства добавляются ребра посредством пересмотра меток вершин. После добавления ребер к подграфу равенства либо увеличивается размер паросочетания (был найден дополняющий путь), либо продолжает расти венгерское дерево. В первом случае этот этап процесса завершается и начинается новый (поскольку размер паросочетания вырос). Во втором случае венгерское дерево растет за счет добавления к нему новых вершин, что, очевидно, не может произойти более n раз.
(Структура венгерского дерева включает исследованные ребра при поиске базисного возможного решения одновременно из всех свободных вершин в S. Когда в T найдена вершина, сопоставленная какой-либо вершине из S, нужно исследовать только соответствующее ребро; однако в S исследуются все ребра, инцидентные этой вершине).
Пусть S – дерево свободных вершин в X. Вырастим венгерские деревья из каждой вершины S. Пусть T – вершины из Y, встретившиеся в поиске дополняющего пути из вершин в S. Добавим все вершины из X, встретившиеся в поиске, в S.
Стоит отметить следующее свойство данного алгоритма:
S
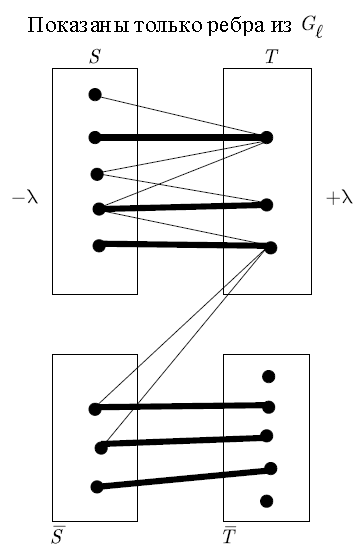
Между S и T не имеется ребер, поскольку в противном случае не было бы возможности полностью вырастить венгерские деревья. Поскольку венгерские деревья выращиваются в G^, альтернативные вершины в поиске помещаются в S и T. Для обновления меток следует взять метки из S и начать равномерно уменьшать их (скажем, на значение A), в то же время увеличивая метки в T на то же значение A. Этот подход гарантирует, что ребра, ведущие из S в T, не исчезнут из подграфа равенства (рис. 1).
Поскольку метки в S уменьшаются, ребра (в графе G), ведущие из S в T, потенциально могут попасть в подграф равенства Gi. По мере увеличения значения A в какой-то момент ребро окажется в подграфе равенства. В этот момент процесс следует остановить и обновить венгерское дерево. Если вершина из T, добавленная к T, сопоставлена с вершиной из S, обе эти вершины перемещаются в S и T, что увеличивает размер венгерского дерева. Если вершина из T свободна, то дополняющий путь найден и данный этап завершен. Этап состоит из таких шагов, выполненных между приращениями размера паросочетания. Поскольку в G всего n вершин, у алгоритма будет не более n этапов, поскольку на каждом этапе размер паросочетания увеличивается на 1. В рамках каждого этапа размер венгерского дерева увеличивается не более n раз. Очевидно, что за время O(n2) можно обнаружить, какое ребро, ведущее из S в T, первым войдет в подграф равенства (для этого нужно просто просмотреть все ребра). Общее время выполнения в таком случае составит O(n4). Теперь покажем, как реализовать это подход за время O(n3).
Задача присваивания, рис. 1
Множества S и T, поддерживаемые алгоритмом
Более эффективная реализация
Определим провис ребра следующим образом: slack(x; y) = l(x) + l(y) - w(x; y) : Тогда Я = min slack(x; y): x2S;y2T
Интуитивно кажется, что вычисление Я требует O(n2) времени. Для каждой вершины y 2 T отметим ребро с минимальным провисом, т.е.
slack[y] = min slack(x; y):
x2S
Вычисление slack[y] для всех y 2 T требует O(n2) времени в начале этапа. По мере продвижения по данному этапу все значения провисов легко обновляются за время O(n), поскольку все они изменяются на одну и ту же величину (метки вершин из S уменьшаются равномерным образом). При перемещении вершины u из S в S необходимо перевычислить провисы вершин в T, что требует O(n) времени. Однако перемещать вершину из S в S можно не более n раз.
Таким образом, каждый этап может быть реализован за время O(n2). Поскольку имеется n этапов, общее время выполнения составляет O(n3). Для разреженных графов есть способ реализации алгоритма с временем выполнения O(n(m + n log n)) с использованием min потоков минимальной стоимости [ ], где m – количество ребер.
Применение
Паросочетание в двудольных графах имеет множество областей применения – например, при планировании заданий единичной длины с целочисленными значениями времени запуска и предельного срока окончания, даже в присутствии штрафных санкций, зависящих от времени.
Открытые вопросы
Необходимо разработать алгоритм с линейным или близким к линейному временем выполнения.
Литература
Некоторые книги, посвященные комбинаторной оптимизации, включают описания алгоритмов поиска паросочетания во взвешенных двудольных графах (см. [2, 5]). Также информацию об этом можно найти в статье Габова [3].
1. Ahuja, R., Magnanti, T., Orlin, J.: Network Flows: Theory, Algorithms and Applications. Prentice Hall, Englewood Cliffs (1993)
2. Cook, W., Cunningham, W., Pulleyblank,W., Schrijver,A.: Combinatorial Optimization. Wiley, New York (1998)
3. Gabow, H.: Data structures for weighted matching and nearest common ancestors with linking. In: Symp. on Discrete Algorithms, 1990, pp. 434-443
4. Kuhn, H.: The Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2,83-97 (1955)
5. Lawler, E.: Combinatorial Optimization: Networks and Matroids. Holt, Rinehart and Winston (1976)
6. Munkres, J.: Algorithms for the assignment and transportation problems. J. Soc. Ind. Appl. Math. 5, 32-38 (1957)