Построение суффиксного дерева в RAM: различия между версиями
Irina (обсуждение | вклад) (Новая страница: «== Ключевые слова и синонимы == Построение полнотекстового индекса Файл:STC_RAM.png») |
Irina (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
Построение полнотекстового индекса | Построение полнотекстового индекса | ||
== Постановка задачи == | |||
Суффиксное дерево – возможно, самая известная и изученная структура данных для индексирования строк, имеющая приложения во многих областях, связанных с анализом последовательностей. После его изобретения в начале семидесятых было разработано несколько подходов к построению суффиксного дерева строки для различных моделей вычислений. Наиболее перспективные подходы, строящие суффиксное дерево в оперативной памяти, представлены в данном обзоре. | |||
Нотация | |||
Пусть дан алфавит £. Trie-деревом над алфавитом £ является корневое дерево, ребра которого помечены строками над S, такими, что никакие две метки ребер, выходящих из одной вершины, не начинаются с одного и того же символа. Trie-дерево является сокращенным, если все его внутренние вершины (возможно, за исключением корня) являются вершинами ветвления. Пусть дана конечная строка S 2 U". Суффиксным деревом S, T(S), сокращенное trie-дерево над S, такое, что конкатенации меток ребер вдоль путей от корня до листьев являются суффиксами S. Пример суффиксного дерева приведен на рис. 1. | |||
[[Файл:STC_RAM.png]] | [[Файл:STC_RAM.png]] | ||
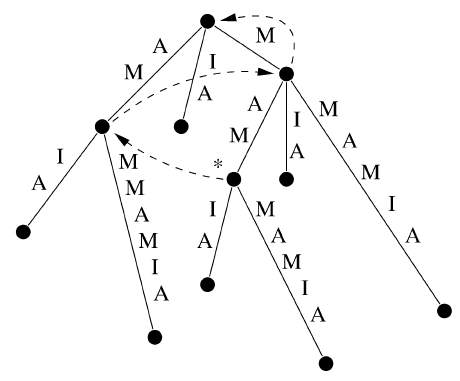
Рисунок 1. Суффиксное дерево для строки S = MAMMAMIA. Пунктирные стрелки обозначают суффиксные ссылки, работающие во всех эффективных алгоритмах построения суффиксного дерева | |||
Конкатенация меток ребер от корня до вершины v дерева T(S) называется меткой пути v и обозначается P(v). Например, метка пути вершины, помеченной звездочкой на рис. 1, равна P(*) = MAM. | |||
Версия от 13:47, 24 июня 2016
Ключевые слова и синонимы
Построение полнотекстового индекса
Постановка задачи
Суффиксное дерево – возможно, самая известная и изученная структура данных для индексирования строк, имеющая приложения во многих областях, связанных с анализом последовательностей. После его изобретения в начале семидесятых было разработано несколько подходов к построению суффиксного дерева строки для различных моделей вычислений. Наиболее перспективные подходы, строящие суффиксное дерево в оперативной памяти, представлены в данном обзоре.
Нотация
Пусть дан алфавит £. Trie-деревом над алфавитом £ является корневое дерево, ребра которого помечены строками над S, такими, что никакие две метки ребер, выходящих из одной вершины, не начинаются с одного и того же символа. Trie-дерево является сокращенным, если все его внутренние вершины (возможно, за исключением корня) являются вершинами ветвления. Пусть дана конечная строка S 2 U". Суффиксным деревом S, T(S), сокращенное trie-дерево над S, такое, что конкатенации меток ребер вдоль путей от корня до листьев являются суффиксами S. Пример суффиксного дерева приведен на рис. 1.
Рисунок 1. Суффиксное дерево для строки S = MAMMAMIA. Пунктирные стрелки обозначают суффиксные ссылки, работающие во всех эффективных алгоритмах построения суффиксного дерева
Конкатенация меток ребер от корня до вершины v дерева T(S) называется меткой пути v и обозначается P(v). Например, метка пути вершины, помеченной звездочкой на рис. 1, равна P(*) = MAM.