Поиск в глубину
Поиск в глубину (Depth first search) — метод систематического прохождения (посещения) вершин графа, когда за счет продвижений от текущей вершины по ребру вперед (к еще непросмотренной вершине) всегда, когда это возможно, и возвратов от текущей вершины по пройденному ребру назад (к ранее пройденной вершине), если движение вперед от текущей вершины невозможно, осуществляется движение по всем вершинам графа, достижимым из заданной вершины [math]\displaystyle{ \,s }[/math], с которой начинается поиск. Поиск в глубину всегда завершается через конечное число шагов в вершине [math]\displaystyle{ \,s }[/math] — начале просмотра; после его завершения все ребра связного графа оказываются разбитыми на два класса: древесные, по которым осуществлялись переходы из посещенных вершин в непосещенные, и ребра касания, замыкающие циклы. Частичный граф, порожденный древесными ребрами, называется деревом поиска в глубину; он является каркасом графа. Нумерация вершин графа в порядке их первого посещения в процессе поиска в глубину называется [math]\displaystyle{ \,M }[/math]-нумерацией. В случае несвязного графа поиск в глубину, завершившийся обходом очередной компоненты связности графа, продолжается с любой еще непросмотренной вершины.
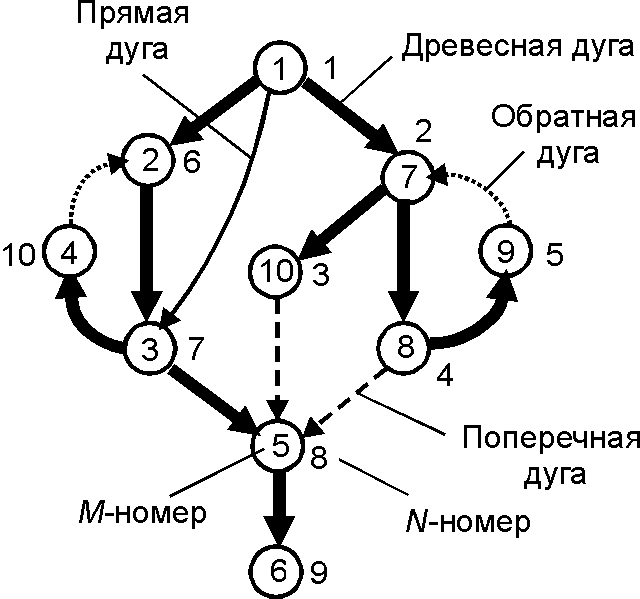
Поиск в глубину в орграфе отличается тем, что при движении вперед дуги проходятся в соответствии с их ориентацией. При этом после завершения пройденные дуги оказываются разбитыми на четыре класса: древесные, прямые, замыкающие какой-либо путь из древесных дуг, обратные, замыкающие контур, и поперечные, ведущие в ранее пройденные вершины и не замыкающие ни контур, ни путь из древесных дуг. Частичный орграф, порожденный древесными дугами, является либо корневым растущим ордеревом (дерево поиска в глубину), либо лесом, каждая компонента которого есть корневое растущее дерево.
Поиск в глубину является основой многих алгоритмов исследования структуры графа.
Другие названия — Возвратный ход, Бектрекинг, Обход графа в глубину.
См. также
- Базисная нумерация,
- [math]\displaystyle{ \,K }[/math]-нумерация,
- [math]\displaystyle{ \,L }[/math]-нумерация,
- [math]\displaystyle{ \,M }[/math]-нумерация,
- [math]\displaystyle{ \,N }[/math]-нумерация,
- [math]\displaystyle{ \,T }[/math]-нумерация,
- Обход графа,
- Поиск в ширину,
- Правильная нумерация,
- Разумная нумерация,
- Топологическая сортировка,
- Укладка уграфа.
Литература
- Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. — М.: Мир, 1979.
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.