K-Унитранзитивный граф: различия между версиями
Перейти к навигации
Перейти к поиску
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
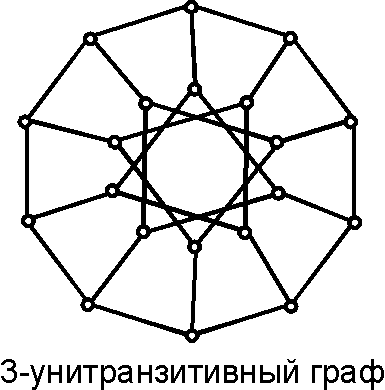
'''<math>k</math>-Унитранзитивный граф''' (''[[k-Unitransitive graph|<math>k</math>-Unitransitive graph]]'') | '''<math>k</math>-Унитранзитивный граф''' (''[[k-Unitransitive graph|<math>k</math>-Unitransitive graph]]'') — [[связный граф|связный]], [[кубический граф|кубический]], <math>k</math>-''транзитивный'' граф, у которого для любых двух <math>k</math>-[[цепь|цепей]] <math>W_{1}</math> и <math>W_{2}</math> существует точно один [[автоморфизм графа|автоморфизм]] <math>\alpha</math> такой, что <math>\alpha W_{1} = W_{2}</math>. | ||
[[связный граф|связный]], [[кубический граф|кубический]], <math>k</math>-''транзитивный'' граф, у которого для | |||
любых двух <math>k</math>-[[цепь|цепей]] <math>W_{1}</math>и <math>W_{2}</math>существует точно один | |||
[[автоморфизм графа|автоморфизм]] <math>\alpha</math> такой, что <math>\alpha W_{1} = W_{2}</math> | |||
[[Файл:k-Unitransitive graph.gif|250px]] | [[Файл:k-Unitransitive graph.gif|250px]] | ||
==См. также == | ==См. также == | ||
''[[k-Транзитивный граф|<math>k</math>-Транзитивный граф]]'' | * ''[[k-Транзитивный граф|<math>k</math>-Транзитивный граф]].'' | ||
==Литература== | ==Литература== | ||
* Харари Ф. Теория графов. — М.: Мир, 1973. | |||
Текущая версия от 04:24, 22 сентября 2011
[math]\displaystyle{ k }[/math]-Унитранзитивный граф ([math]\displaystyle{ k }[/math]-Unitransitive graph) — связный, кубический, [math]\displaystyle{ k }[/math]-транзитивный граф, у которого для любых двух [math]\displaystyle{ k }[/math]-цепей [math]\displaystyle{ W_{1} }[/math] и [math]\displaystyle{ W_{2} }[/math] существует точно один автоморфизм [math]\displaystyle{ \alpha }[/math] такой, что [math]\displaystyle{ \alpha W_{1} = W_{2} }[/math].
См. также
Литература
- Харари Ф. Теория графов. — М.: Мир, 1973.