Экзистенциальный граф: различия между версиями
Tanya (обсуждение | вклад) (Новая страница: «'''Экзистенциальные графы''' (''Existential graphs (EGs)'') – это графический (диаграмматич…») |
Tanya (обсуждение | вклад) Нет описания правки |
||
| Строка 5: | Строка 5: | ||
'''Альфа''' | '''Альфа''' | ||
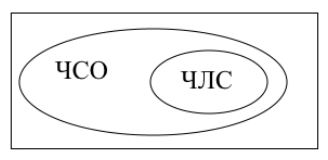
На альфа уровне мы работаем с плоскостью и разрезами, правила преобразования которых позволяют построить теорию, дедуктивно эквивалентную логике высказываний. Два [[ | На альфа уровне мы работаем с плоскостью и разрезами, правила преобразования которых позволяют построить теорию, дедуктивно эквивалентную логике высказываний. Два [[граф]]а на плоскости соответствуют булевой конъюнкции, а круговой разрез — булеву отрицанию (пример на рис. 1). | ||
[[Файл:Ris1.JPG]] | |||
Рис. 1. «Если человек смотрит олимпиаду (ЧСО), то он любит спорт (ЧЛС)» или «Неверно, что человек смотрит олимпиаду (ЧСО), и он не любит спорт (ЧЛС)» | Рис. 1. «Если человек смотрит олимпиаду (ЧСО), то он любит спорт (ЧЛС)» или «Неверно, что человек смотрит олимпиаду (ЧСО), и он не любит спорт (ЧЛС)» | ||
| Строка 12: | Строка 14: | ||
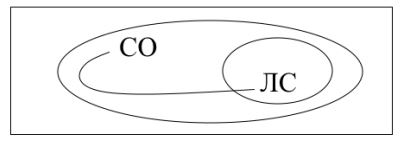
На бета уровне разрезы дополняются линией тождества, которая является диаграмматическим аналогом равенства, предикации, экзистенциальной квантификации (пример на рис. 2). Ее пустые концы указывают на местность отношений. По своим дедуктивным возможностям раздел сопоставим с исчислением первого порядка с равенством. | На бета уровне разрезы дополняются линией тождества, которая является диаграмматическим аналогом равенства, предикации, экзистенциальной квантификации (пример на рис. 2). Ее пустые концы указывают на местность отношений. По своим дедуктивным возможностям раздел сопоставим с исчислением первого порядка с равенством. | ||
[[Файл:Ris2.JPG]] | |||
Рис. 2. «Всякий, кто смотрит олимпиаду, любит спорт» | Рис. 2. «Всякий, кто смотрит олимпиаду, любит спорт» | ||
| Строка 18: | Строка 22: | ||
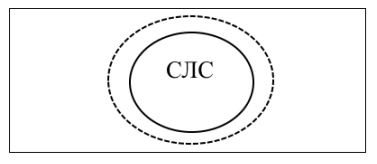
С последним разделом ситуация не столь однозначна: «Раздел гамма находится в состоянии младенчества. Пройдут годы, прежде чем мои последователи смогут привести его в состояние, в которое приведены части альфа и бета». По задумке он должен был предложить современную теорию модальностей, а также теорию высших порядков. Для достижения этой цели Пирс вводит пунктирную круговую схему (сломанный разрез), позволяющую вводить модальность возможности «возможно не». | С последним разделом ситуация не столь однозначна: «Раздел гамма находится в состоянии младенчества. Пройдут годы, прежде чем мои последователи смогут привести его в состояние, в которое приведены части альфа и бета». По задумке он должен был предложить современную теорию модальностей, а также теорию высших порядков. Для достижения этой цели Пирс вводит пунктирную круговую схему (сломанный разрез), позволяющую вводить модальность возможности «возможно не». | ||
[[Файл:Ris3.JPG]] | |||
Рис. 3. «Возможно, что Саша любит спорт (СЛС)» | Рис. 3. «Возможно, что Саша любит спорт (СЛС)» | ||
| Строка 44: | Строка 50: | ||
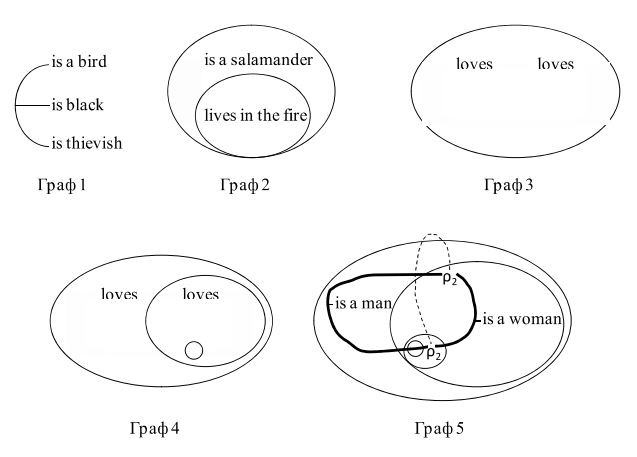
Примеры: бета-граф — граф 1 представляет собой утверждение «Некоторые черные птицы вороваты», а граф 2 представляет собой утверждение «Все саламандры живут в огне». Здесь места отмечены лингвистическими ремами (linguistic rhemas), такими как «____является саламандрой», у которых на одном изгибе расположена линия тождества. Граф 3 очень удобен для изображения обобщающей квантификации в высказывании «Никакие два человека не любят друг друга», в то время как граф 4, в котором линия тождества, выражающая рефлексивную конструкцию, разрезана, утверждает, что «Никто не любит того, кто не любит кого-то другого». | Примеры: бета-граф — граф 1 представляет собой утверждение «Некоторые черные птицы вороваты», а граф 2 представляет собой утверждение «Все саламандры живут в огне». Здесь места отмечены лингвистическими ремами (linguistic rhemas), такими как «____является саламандрой», у которых на одном изгибе расположена линия тождества. Граф 3 очень удобен для изображения обобщающей квантификации в высказывании «Никакие два человека не любят друг друга», в то время как граф 4, в котором линия тождества, выражающая рефлексивную конструкцию, разрезана, утверждает, что «Никто не любит того, кто не любит кого-то другого». | ||
[[Файл:Egs.JPG]] | |||
Правила вывода представляют собой хирургические операции в смысле полного набора переходов, выражающих выведение заключений: | Правила вывода представляют собой хирургические операции в смысле полного набора переходов, выражающих выведение заключений: | ||
Текущая версия от 07:58, 2 июня 2017
Экзистенциальные графы (Existential graphs (EGs)) – это графический (диаграмматический) способ представления логических выражений, предложенный американским философом, логиком и математиком Чарльзом Пирсом (Charles Peirce) в период с 1896 по 1911 г. Это наиболее ранняя работа, имеющая прямое влияние на современные семантические сети.
Система логики Пирса состоит из трех частей – «альфа», «бета» и «гамма». Подсистема «альфа» является логикой высказываний, подсистема «бета» – логикой предикатов первого порядка без функциональных символов, а подсистема «гамма» – формализацией модальной логики с кванторами и логики предикатов высших порядков.
Альфа
На альфа уровне мы работаем с плоскостью и разрезами, правила преобразования которых позволяют построить теорию, дедуктивно эквивалентную логике высказываний. Два графа на плоскости соответствуют булевой конъюнкции, а круговой разрез — булеву отрицанию (пример на рис. 1).
Рис. 1. «Если человек смотрит олимпиаду (ЧСО), то он любит спорт (ЧЛС)» или «Неверно, что человек смотрит олимпиаду (ЧСО), и он не любит спорт (ЧЛС)»
Бета
На бета уровне разрезы дополняются линией тождества, которая является диаграмматическим аналогом равенства, предикации, экзистенциальной квантификации (пример на рис. 2). Ее пустые концы указывают на местность отношений. По своим дедуктивным возможностям раздел сопоставим с исчислением первого порядка с равенством.
Рис. 2. «Всякий, кто смотрит олимпиаду, любит спорт»
Гамма
С последним разделом ситуация не столь однозначна: «Раздел гамма находится в состоянии младенчества. Пройдут годы, прежде чем мои последователи смогут привести его в состояние, в которое приведены части альфа и бета». По задумке он должен был предложить современную теорию модальностей, а также теорию высших порядков. Для достижения этой цели Пирс вводит пунктирную круговую схему (сломанный разрез), позволяющую вводить модальность возможности «возможно не».
Рис. 3. «Возможно, что Саша любит спорт (СЛС)»
Позднее сломанный разрез заменяется системой тинктур, то есть оттенков, в которые способна окрашиваться плоскость. Введение оттенков позволяет типизировать пространство, что, в свою очередь, дает возможность говорить о мультимодальности. Пирс выделяет 12 тинктур, хотя откуда берется это количество и как именно с ним следует работать, непонятно и сегодня. Концепция явно не была завершена, а потому делать какие-то выводы довольно сложно.
Синтаксис экзистенциальных графов состоит из:
(1) доски утверждений (sheet of assertion (SA)), представляющей собой универсум дискурса,
(2) взаимного расположения графов на доске утверждений и
(3) разреза (cut), вырезающего граф из доски утверждений SA.
Это формирует альфа систему, а в бета системе добавляются:
(4) линия тождества (LI) и
(5) места (spots).
Пирс называет ветвящуюся линию, или линию, которая пересекает разрезы, лигатурой (ligature). Места представляют собой простые содержательные области доски утверждений SA. Линии тождества (LIs) соединяют области графов — свободные оконечности внутри разрезов, и места — линии, соединенные с изгибами, удаленными от мест. Благодаря взаимному расположению графов относительно друг друга и разрезам, информация, содержащая дизъюнкции и условные высказывания («спирали»), легко схватывается. Отрицательные и утвердительные области (области, вложенные в нечетное или четное количество разрезов) разделяют кванторы всеобщности и существования.
В рамках гамма системы добавляется ряд новых символов, таких как «пунктирный разрез» (broken cut) для модального оператора или специальные места и линии тождества для обобщения и умозаключений высшего порядка.
Примеры: бета-граф — граф 1 представляет собой утверждение «Некоторые черные птицы вороваты», а граф 2 представляет собой утверждение «Все саламандры живут в огне». Здесь места отмечены лингвистическими ремами (linguistic rhemas), такими как «____является саламандрой», у которых на одном изгибе расположена линия тождества. Граф 3 очень удобен для изображения обобщающей квантификации в высказывании «Никакие два человека не любят друг друга», в то время как граф 4, в котором линия тождества, выражающая рефлексивную конструкцию, разрезана, утверждает, что «Никто не любит того, кто не любит кого-то другого».
Правила вывода представляют собой хирургические операции в смысле полного набора переходов, выражающих выведение заключений:
(1) двойной разрез можно добавить и стереть;
(2) в утвердительной области можно стереть любой граф или часть линии тождества;
(3) в отрицательной части можно добавить любой граф или восстановить пунктирную линию тождества;
(4) копию графа можно поместить внутри той же области или любой вложенной в него области, и, наоборот, любое действие, являющееся следствием итерации, можно отменить, т. е. копии графов можно удалить.
Литература
• Peirce, C.S., Collected Papers of Charles Sanders Peirce. Eight volumes, Arthur W. Burks, Charles Hartshornce, and Paul Weiss (eds.). Cambridge, Harvard University Press, 1931—1958.
• Peirce C.S. Manuscripts in the Houghton Library of Harvard University, as identified by Richard Robin // Annotated Catalogue of the Papers of Charles S. Peirce. Amherst, 1967.
• Pietarinen A.-V. , «Existential Graphs: What the Diagrammatic Logic of Cognition Might Look Like», History and Philosophy of Logic, 32(3), pp. 265–281, 2011.
• Roberts, D., The Existential Graphs of Charles S. Peirce, The Hague, Paris, Mouton, 1973.
• Sowa, J., Cognitive Architectures For Conceptual Structures, in S. Andrews, S. Polovina, R. Hill, & B. Akhgar (eds.), 19th International Conference on Conceptual Structures, pp. 35—49, Heidelberg, Springer, 2011.
• Zeman Jay J. The Graphical Logic of C.S. Peirce: dissertation. Chicago, 1964 (Online edition, 2002, at http://web.clas.ufl.edu/users/jzeman/)
• Боброва А.С. Теория рассуждений Ч. Пирса. Москва, 2005.