Аранжируемый граф: различия между версиями
Перейти к навигации
Перейти к поиску
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
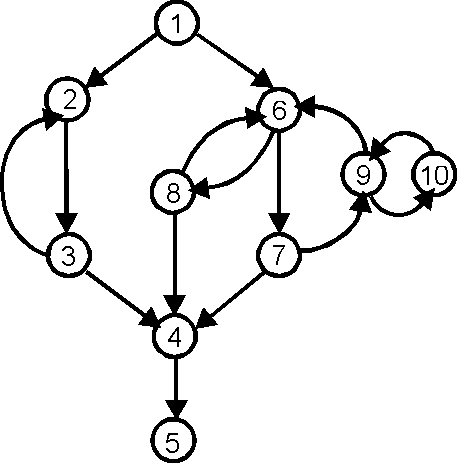
'''Аранжируемый граф''' (''[[Arrangeable graph]]'') | '''Аранжируемый граф''' (''[[Arrangeable graph]]'') — ''[[управляющий граф]]'' (в общем случае [[орграф]] с одним [[вход|входом]]), допускающий [[аранжировка|''аранжировку'']]; аранжируемость эквивалентна [[регуляризуемый граф|регуляризуемости графа]] и является одной из важнейших характеристик [[управляющий граф|управляющего графа]]. | ||
[[Файл:Arrangeable graph.png|300px]] | [[Файл:Arrangeable graph.png|300px]] | ||
| Строка 12: | Строка 12: | ||
==Литература== | ==Литература== | ||
* Касьянов В.Н. Оптимизирующие преобразования программ. | * Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | ||
* Евстигнеев В.А. Применение теории графов в программировании. | * Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985. | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. | * Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | ||
Версия от 09:11, 18 ноября 2010
Аранжируемый граф (Arrangeable graph) — управляющий граф (в общем случае орграф с одним входом), допускающий аранжировку; аранжируемость эквивалентна регуляризуемости графа и является одной из важнейших характеристик управляющего графа.
См. также
- Запрещенный подграф,
- Одновходовый граф,
- Разборный граф,
- Регуляризуемый граф,
- Сводимый управляющий граф.
Литература
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.
- Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985.
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.