Равнодоступная адресная машина: различия между версиями
KVN (обсуждение | вклад) |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
'''Равнодоступная адресная машина''' ([[Random access machine|''Random access machine, RAM'']]) | '''Равнодоступная адресная машина''' ([[Random access machine|''Random access machine, RAM'']]) — универсальная математическая модель вычислений, которая является хорошим приближением к классу обычных, традиционных вычислительных машин с точки зрения отражения затрат времени и памяти при представлении данных и алгоритмов, целиком помещающихся в оперативной памяти. | ||
'''Равнодоступная адресная машина''' моделирует вычислительную машину с одним сумматором, в которой команды программы не могут изменять сами себя. | '''Равнодоступная адресная машина''' моделирует вычислительную машину с одним сумматором, в которой команды программы не могут изменять сами себя. | ||
| Строка 5: | Строка 5: | ||
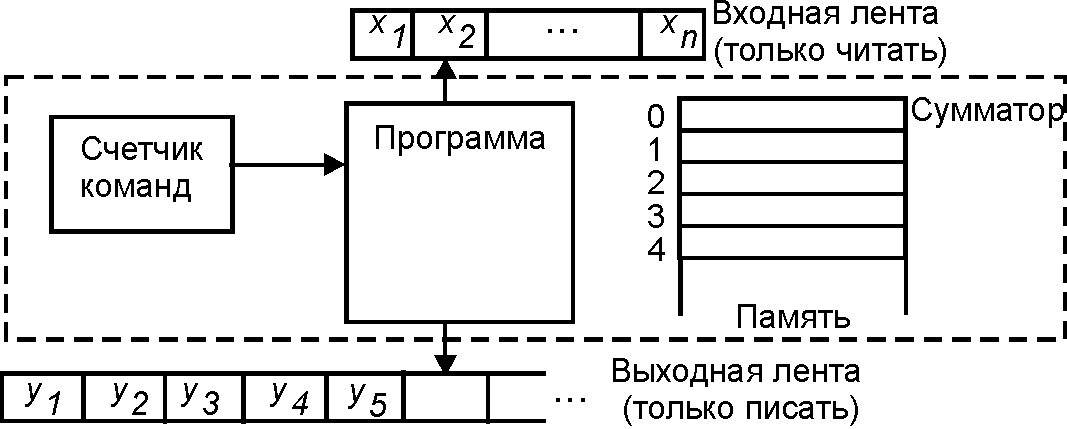
'''Равнодоступная адресная машина''' состоит из входной ленты, с которой она может только считывать, выходной ленты, на которую она может только записывать, и памяти. | '''Равнодоступная адресная машина''' состоит из входной ленты, с которой она может только считывать, выходной ленты, на которую она может только записывать, и памяти. | ||
Входная лента | Входная лента — это последовательность клеток, содержащих записи целых чисел и доступных для считывания по одной в соответствии с их упорядоченностью. Она состоит из неограниченной последовательности клеток, которые вначале все пусты; при выполнении команды записи происходит печать целого числа в первой свободной клетке выходной ленты. | ||
Память | Память — это последовательность подряд пронумерованных ячеек, каждая из которых способна хранить двоичную запись произвольного целого числа. Обращение к значению, хранимому в некоторой ячейке, осуществляется по адресу (номеру) этой | ||
ячейки. Ячейка с номером 0 называется ''сумматором''. Адресация может быть не только ''абсолютной'', когда явно | ячейки. Ячейка с номером 0 называется ''сумматором''. Адресация может быть не только ''абсолютной'', когда явно | ||
указывается номер ячейки, но и косвенной. При ''косвенной адресации'' указывается адрес некоторой другой ячейки | указывается номер ячейки, но и косвенной. При ''косвенной адресации'' указывается адрес некоторой другой ячейки | ||
| Строка 13: | Строка 13: | ||
адреса адресуемой ячейки. | адреса адресуемой ячейки. | ||
Состояние памяти | Состояние памяти — это отображение <math>\,W</math> адресов в двоичные слова, сопоставляющее с каждым адресом <math>\,n</math> то слово <math>\,W(n)</math>, которое ''хранится (содержится)'' в ячейке с адресом <math>\,n</math>. | ||
слово <math>W(n)</math>, которое ''хранится (содержится)'' в ячейке с адресом <math>n</math>. | |||
Программа | Программа — это конечная последовательность команд, занумерованных числами <math>1,2,3,\ldots</math>. Счетчик команд — это переменная, принимающая значение из множества неотрицательных целых чисел. | ||
команд | |||
Состояние вычисления (конфигурация) | Состояние вычисления (конфигурация) — это четверка <math>\,(x, W, k, y)</math>, где <math>\,x</math> — непрочитанная часть входной ленты, <math>\,W</math> — состояние памяти, <math>\,k</math> — значение счетчика команд, а <math>\,y</math> — заполненная часть входной ленты. | ||
Выполнение '''равнодоступной адресной машины''' начинается с выполнения первой команды программы, нормально завершается выполнением команды останова и описывается протоколом выполнения | Выполнение '''равнодоступной адресной машины''' начинается с выполнения первой команды программы, нормально завершается выполнением команды останова и описывается протоколом выполнения — последовательностью конфигураций, в которой конфигурация <math>\,(x, W, 1, e)</math>, где <math>\,x</math> — вход, <math>\,e</math> — пустая цепочка и <math>\,W(k) = 0</math> для любого <math>\,k</math>, является первой (начальной), а каждая следующая конфигурация, если она имеется, получается из текущей выполнением команды, номер которой указан в текущей конфигурации. Конфигурация, в которой счетчик команд равен нулю (ошибочная конфигурация) или номеру команды останова, может быть только последней (заключительной) конфигурацией протокола выполнения. Если выполнение '''равнодоступной адресной машины''' нормально завершается, то его результат — запись на выходной ленте, находящейся слева от печатающей головки. | ||
Каждая команда '''равнодоступной адресной машины''' имеет имя (код операции) и операнд. Операнд может быть одного из следующих типов: "<math>=i</math>" | Каждая команда '''равнодоступной адресной машины''' имеет имя (код операции) и операнд. Операнд может быть одного из следующих типов: "<math>\,=i</math>" — означает само число <math>\,i</math> и называется литералом; "<math>\,i</math>" — содержимое ячейки <math>\,i</math>; "<math>\,*i</math>" — используется для косвенной адресации, т.е. значением операнда служит содержимое ячейки, адрес которой имеется в ячейке с номером <math>\,i</math>. Обозначая через <math>\,V(a)</math> значение операнда <math>\,a</math>, получаем: <math>\,V(=i)=i</math>; <math>\,V(i) =W(i)</math> и <math>\,V(*i)=W(W(i))</math>, где <math>\,W</math> — текущее состояние памяти. Набор команд '''равнодоступной адресной машины''' традиционен для реальных ЭВМ и состоит из команд считывания и запоминания, арифметических и логических команд, команд перехода, команд ввода и вывода и команды останова. | ||
Модель вычислительной машины, получившая название [[равнодоступной адресной машины с хранимой программой|''равнодоступной адресной машины с хранимой программой'']] (или [[РАСП]]), отличается от '''равнодоступной адресной машины''' лишь тем, что ее программа находится в памяти и может изменять себя. | Модель вычислительной машины, получившая название [[равнодоступной адресной машины с хранимой программой|''равнодоступной адресной машины с хранимой программой'']] (или [[РАСП]]), отличается от '''равнодоступной адресной машины''' лишь тем, что ее программа находится в памяти и может изменять себя. | ||
Как при равномерном, так и при логарифмическом весах команд для любой '''равнодоступной адресной машины''' (соответственно ''РАСП'') с временной сложностью <math>T(n)</math> существует такая постоянная <math>k</math>, что найдется эквивалентная ''РАСП'' (соответственно ''РАМ'' ), временная сложность которой не превосходит <math> kT(n)</math>. | Как при равномерном, так и при логарифмическом весах команд для любой '''равнодоступной адресной машины''' (соответственно ''РАСП'') с временной сложностью <math>\,T(n)</math> существует такая постоянная <math>\,k</math>, что найдется эквивалентная ''РАСП'' (соответственно ''РАМ'' ), временная сложность которой не превосходит <math> \,kT(n)</math>. | ||
[[Недетерминированная равнодоступная адресная машина]] (или [[НРАМ]]) получается из '''равнодоступной адресной машины''' добавлением команды ВЫБОР<math> (L_1,L_2,\ldots, L_r)</math>, означающей, что недетерминированы выбор и последующее выполнение одного из операторов <math>L_1,L_2,\ldots,L_r.</math> | [[Недетерминированная равнодоступная адресная машина]] (или [[НРАМ]]) получается из '''равнодоступной адресной машины''' добавлением команды ВЫБОР<math> (L_1,L_2,\ldots, L_r)</math>, означающей, что недетерминированы выбор и последующее выполнение одного из операторов <math>L_1,L_2,\ldots,L_r.</math> | ||
Другие названия | Другие названия — [[Машина с произвольным доступом к памяти]], [[РАМ]]. | ||
| Строка 41: | Строка 39: | ||
==Литература== | ==Литература== | ||
* Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. — М.: Мир, 1979. | |||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
* Касьянов В.Н. Лекции по теории формальных языков, автоматов и сложности вычислений. — Новосибирск: НГУ, 1995. | |||
Версия от 06:25, 13 июля 2011
Равнодоступная адресная машина (Random access machine, RAM) — универсальная математическая модель вычислений, которая является хорошим приближением к классу обычных, традиционных вычислительных машин с точки зрения отражения затрат времени и памяти при представлении данных и алгоритмов, целиком помещающихся в оперативной памяти.
Равнодоступная адресная машина моделирует вычислительную машину с одним сумматором, в которой команды программы не могут изменять сами себя.
Равнодоступная адресная машина состоит из входной ленты, с которой она может только считывать, выходной ленты, на которую она может только записывать, и памяти.
Входная лента — это последовательность клеток, содержащих записи целых чисел и доступных для считывания по одной в соответствии с их упорядоченностью. Она состоит из неограниченной последовательности клеток, которые вначале все пусты; при выполнении команды записи происходит печать целого числа в первой свободной клетке выходной ленты.
Память — это последовательность подряд пронумерованных ячеек, каждая из которых способна хранить двоичную запись произвольного целого числа. Обращение к значению, хранимому в некоторой ячейке, осуществляется по адресу (номеру) этой ячейки. Ячейка с номером 0 называется сумматором. Адресация может быть не только абсолютной, когда явно указывается номер ячейки, но и косвенной. При косвенной адресации указывается адрес некоторой другой ячейки (называемой ссылкой, или указателем), содержимое которой рассматривается в качестве абсолютного адреса адресуемой ячейки.
Состояние памяти — это отображение [math]\displaystyle{ \,W }[/math] адресов в двоичные слова, сопоставляющее с каждым адресом [math]\displaystyle{ \,n }[/math] то слово [math]\displaystyle{ \,W(n) }[/math], которое хранится (содержится) в ячейке с адресом [math]\displaystyle{ \,n }[/math].
Программа — это конечная последовательность команд, занумерованных числами [math]\displaystyle{ 1,2,3,\ldots }[/math]. Счетчик команд — это переменная, принимающая значение из множества неотрицательных целых чисел.
Состояние вычисления (конфигурация) — это четверка [math]\displaystyle{ \,(x, W, k, y) }[/math], где [math]\displaystyle{ \,x }[/math] — непрочитанная часть входной ленты, [math]\displaystyle{ \,W }[/math] — состояние памяти, [math]\displaystyle{ \,k }[/math] — значение счетчика команд, а [math]\displaystyle{ \,y }[/math] — заполненная часть входной ленты.
Выполнение равнодоступной адресной машины начинается с выполнения первой команды программы, нормально завершается выполнением команды останова и описывается протоколом выполнения — последовательностью конфигураций, в которой конфигурация [math]\displaystyle{ \,(x, W, 1, e) }[/math], где [math]\displaystyle{ \,x }[/math] — вход, [math]\displaystyle{ \,e }[/math] — пустая цепочка и [math]\displaystyle{ \,W(k) = 0 }[/math] для любого [math]\displaystyle{ \,k }[/math], является первой (начальной), а каждая следующая конфигурация, если она имеется, получается из текущей выполнением команды, номер которой указан в текущей конфигурации. Конфигурация, в которой счетчик команд равен нулю (ошибочная конфигурация) или номеру команды останова, может быть только последней (заключительной) конфигурацией протокола выполнения. Если выполнение равнодоступной адресной машины нормально завершается, то его результат — запись на выходной ленте, находящейся слева от печатающей головки.
Каждая команда равнодоступной адресной машины имеет имя (код операции) и операнд. Операнд может быть одного из следующих типов: "[math]\displaystyle{ \,=i }[/math]" — означает само число [math]\displaystyle{ \,i }[/math] и называется литералом; "[math]\displaystyle{ \,i }[/math]" — содержимое ячейки [math]\displaystyle{ \,i }[/math]; "[math]\displaystyle{ \,*i }[/math]" — используется для косвенной адресации, т.е. значением операнда служит содержимое ячейки, адрес которой имеется в ячейке с номером [math]\displaystyle{ \,i }[/math]. Обозначая через [math]\displaystyle{ \,V(a) }[/math] значение операнда [math]\displaystyle{ \,a }[/math], получаем: [math]\displaystyle{ \,V(=i)=i }[/math]; [math]\displaystyle{ \,V(i) =W(i) }[/math] и [math]\displaystyle{ \,V(*i)=W(W(i)) }[/math], где [math]\displaystyle{ \,W }[/math] — текущее состояние памяти. Набор команд равнодоступной адресной машины традиционен для реальных ЭВМ и состоит из команд считывания и запоминания, арифметических и логических команд, команд перехода, команд ввода и вывода и команды останова.
Модель вычислительной машины, получившая название равнодоступной адресной машины с хранимой программой (или РАСП), отличается от равнодоступной адресной машины лишь тем, что ее программа находится в памяти и может изменять себя.
Как при равномерном, так и при логарифмическом весах команд для любой равнодоступной адресной машины (соответственно РАСП) с временной сложностью [math]\displaystyle{ \,T(n) }[/math] существует такая постоянная [math]\displaystyle{ \,k }[/math], что найдется эквивалентная РАСП (соответственно РАМ ), временная сложность которой не превосходит [math]\displaystyle{ \,kT(n) }[/math].
Недетерминированная равнодоступная адресная машина (или НРАМ) получается из равнодоступной адресной машины добавлением команды ВЫБОР[math]\displaystyle{ (L_1,L_2,\ldots, L_r) }[/math], означающей, что недетерминированы выбор и последующее выполнение одного из операторов [math]\displaystyle{ L_1,L_2,\ldots,L_r. }[/math]
Другие названия — Машина с произвольным доступом к памяти, РАМ.
См. также
Литература
- Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. — М.: Мир, 1979.
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.
- Касьянов В.Н. Лекции по теории формальных языков, автоматов и сложности вычислений. — Новосибирск: НГУ, 1995.