Регуляризуемый граф: различия между версиями
Glk (обсуждение | вклад) (Создана новая страница размером '''Регуляризуемый граф''' (''Regularizable graph'') - ''уграф'' <math>G</math>, для которого сущес...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
'''Регуляризуемый граф''' (''Regularizable graph'') - | '''Регуляризуемый граф''' (''[[Regularizable graph]]'') - | ||
''уграф'' <math>G</math>, для которого существует такая | ''[[уграф]]'' <math>G</math>, для которого существует такая | ||
последовательность уграфов | последовательность уграфов | ||
<math>G_0=G,G_1,\ldots,G_l,</math> | <math>G_0=G,G_1,\ldots,G_l,</math> | ||
что <math>G_l</math> --- ''тривиальный'' уграф, а каждый | что <math>G_l</math> --- ''[[тривиальный граф|тривиальный]]'' уграф, а каждый | ||
<math>G_i</math>, <math>i>0</math>, является ''фактор-уграфом'' уграфа <math>G_{i-1}</math> | <math>G_i</math>, <math>i>0</math>, является ''[[фактор-уграф|фактор-уграфом]]'' уграфа <math>G_{i-1}</math> | ||
относительно некоторого множества попарно непересекающихся | относительно некоторого множества попарно непересекающихся | ||
''интервалов''. | ''[[интервал|интервалов]]''. | ||
[[Файл:Regularizable graph.png]] | |||
Справедлива | Справедлива | ||
теорема Касьянова---Хехта---Ульмана о том, что | теорема Касьянова---Хехта---Ульмана о том, что | ||
''уграф регуляризуем тогда и только тогда, когда выполняется любое из следующих свойств: <math>G</math> --- сводим, <math>G</math> --- аранжируем, <math>G</math> --- разборный, <math>G</math> --- одновходовый, <math>G</math> не содержит запрещенного подграфа, <math>G</math> имеет единственный каркас.'' | ''уграф регуляризуем тогда и только тогда, когда выполняется любое из следующих свойств: <math>G</math> --- [[сводимый уграф|сводим]], <math>G</math> --- [[аранжируемый граф|аранжируем]], <math>G</math> --- [[разборный граф|разборный]], <math>G</math> --- [[одновходовый граф|одновходовый]], <math>G</math> не содержит [[запрещенный подграф|запрещенного подграфа]], <math>G</math> имеет единственный [[каркас]].'' | ||
Большинство современных языков высокого уровня являются | Большинство современных языков высокого уровня являются | ||
| Строка 21: | Строка 23: | ||
Фортран-программ показывают, что <math>90\%</math> уграфов регуляризуемы, | Фортран-программ показывают, что <math>90\%</math> уграфов регуляризуемы, | ||
причем в среднем зоны занимают небольшую часть программы | причем в среднем зоны занимают небольшую часть программы | ||
(около <math>4\%</math>). С другой стороны, существует алгоритм, который | (около <math>4\%</math>). С другой стороны, существует [[алгоритм]], который | ||
эквивалентными дублированиями преобразует любой уграф <math>G</math> в | эквивалентными дублированиями преобразует любой уграф <math>G</math> в | ||
такой регуляризуемый уграф, в котором имеется не более чем | такой регуляризуемый уграф, в котором имеется не более чем | ||
<math>2^{\min(m(p),k(p))}</math> экземпляров любой вершины <math>p</math> уграфа | <math>2^{\min(m(p),k(p))}</math> экземпляров любой [[вершина|вершины]] <math>p</math> уграфа | ||
<math>G</math>, <math>m(p)</math> --- количество различных ''многовходовых зон'' | <math>G</math>, <math>m(p)</math> --- количество различных ''многовходовых зон'' | ||
уграфа <math>G</math>, содержащих <math>p</math>, а <math>k(p)</math> --- минимальное такое | уграфа <math>G</math>, содержащих <math>p</math>, а <math>k(p)</math> --- минимальное такое | ||
| Строка 37: | Строка 39: | ||
сохранении времени счета по программе. | сохранении времени счета по программе. | ||
Другое название --- ''Обобщенно-сводимый уграф.'' | Другое название --- ''[[Обобщенно-сводимый уграф]].'' | ||
См. также ''Аранжируемый граф, Запрещенный подграф, Каркас уграфа Одновходовый граф, Разборный граф, Сводимый управляющий граф.'' | ==См. также== | ||
''[[Аранжируемый граф]], [[Запрещенный подграф]], [[Каркас уграфа]], [[Одновходовый граф]], [[Разборный граф]], [[Сводимый управляющий граф]].'' | |||
==Литература== | ==Литература== | ||
[Касьянов/88], | [Касьянов/88], | ||
Версия от 05:59, 25 января 2010
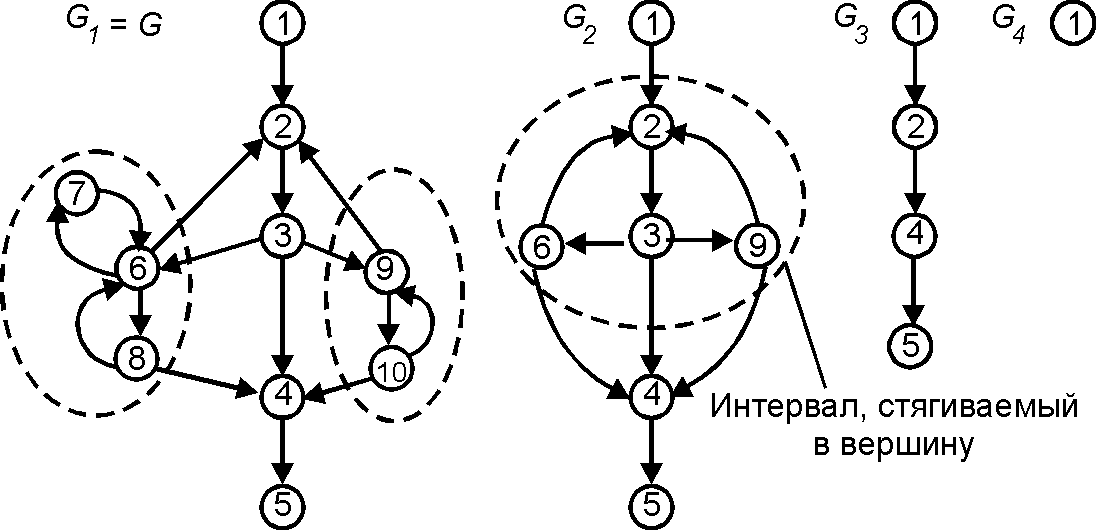
Регуляризуемый граф (Regularizable graph) - уграф [math]\displaystyle{ G }[/math], для которого существует такая последовательность уграфов
[math]\displaystyle{ G_0=G,G_1,\ldots,G_l, }[/math]
что [math]\displaystyle{ G_l }[/math] --- тривиальный уграф, а каждый [math]\displaystyle{ G_i }[/math], [math]\displaystyle{ i\gt 0 }[/math], является фактор-уграфом уграфа [math]\displaystyle{ G_{i-1} }[/math] относительно некоторого множества попарно непересекающихся интервалов.
Справедлива теорема Касьянова---Хехта---Ульмана о том, что уграф регуляризуем тогда и только тогда, когда выполняется любое из следующих свойств: [math]\displaystyle{ G }[/math] --- сводим, [math]\displaystyle{ G }[/math] --- аранжируем, [math]\displaystyle{ G }[/math] --- разборный, [math]\displaystyle{ G }[/math] --- одновходовый, [math]\displaystyle{ G }[/math] не содержит запрещенного подграфа, [math]\displaystyle{ G }[/math] имеет единственный каркас.
Большинство современных языков высокого уровня являются языками структурного программирования и, таким образом, ориентированными на написание регуляризуемых программ. Что касается других языков, основным из которых является Фортран, то исследования характеристик реальных Фортран-программ показывают, что [math]\displaystyle{ 90\% }[/math] уграфов регуляризуемы, причем в среднем зоны занимают небольшую часть программы (около [math]\displaystyle{ 4\% }[/math]). С другой стороны, существует алгоритм, который эквивалентными дублированиями преобразует любой уграф [math]\displaystyle{ G }[/math] в такой регуляризуемый уграф, в котором имеется не более чем [math]\displaystyle{ 2^{\min(m(p),k(p))} }[/math] экземпляров любой вершины [math]\displaystyle{ p }[/math] уграфа [math]\displaystyle{ G }[/math], [math]\displaystyle{ m(p) }[/math] --- количество различных многовходовых зон уграфа [math]\displaystyle{ G }[/math], содержащих [math]\displaystyle{ p }[/math], а [math]\displaystyle{ k(p) }[/math] --- минимальное такое число, что имеется множество, состоящее из [math]\displaystyle{ k(p) }[/math] вершин и включающее хотя бы по одной вершине каждой из тех многовходовых зон уграфа [math]\displaystyle{ G }[/math], которые целиком лежат в максимальной многовходовой зоне, содержащей вершину [math]\displaystyle{ p }[/math]. Поэтому в реальных случаях даже для языков "неструктурного" программирования, как правило, уграф регуляризуем, а если нет, то его преобразование для получения регуляризуемости не потребует даже двукратного увеличения его размера при сохранении времени счета по программе.
Другое название --- Обобщенно-сводимый уграф.
См. также
Аранжируемый граф, Запрещенный подграф, Каркас уграфа, Одновходовый граф, Разборный граф, Сводимый управляющий граф.
Литература
[Касьянов/88],
[Евстигнеев-Касьянов/94],
[Касьянов/86]