Граф ближайших соседей: различия между версиями
Перейти к навигации
Перейти к поиску
KVN (обсуждение | вклад) (Новая страница: «'''Граф ближайших соседей''' (''Nearest neighbor graph'') для множества ''P'', состоящего из ''n'' объектов в метрическом пространстве (например, для множества точек на плоскости с евклидовой метрикой) — это ориентированный граф, вершинами которого служат элементы мно...») |
KVN (обсуждение | вклад) Нет описания правки |
||
| Строка 2: | Строка 2: | ||
Во многих обсуждениях направление рёбер игнорируется и '''граф ближайших соседей''' определяется как обычный (неориентированный) [[граф]]. Однако отношение ближайшего соседства не является симметричным, т. е. если ''q'' является ближайшим соседом ''p'', то ''p'' не обязательно будет ближайшим соседом ''q''. | Во многих обсуждениях направление рёбер игнорируется и '''граф ближайших соседей''' определяется как обычный (неориентированный) [[граф]]. Однако отношение ближайшего соседства не является симметричным, т. е. если ''q'' является ближайшим соседом ''p'', то ''p'' не обязательно будет ближайшим соседом ''q''. | ||
[[Файл:Nearest neighbor graph.png|275px]] | |||
[[Категория: Обыкновенные графы]] | [[Категория: Обыкновенные графы]] | ||
[[Категория: Ориентированные графы]] | [[Категория: Ориентированные графы]] | ||
[[Категория:Неориентированные графы]] | |||
Текущая версия от 10:50, 25 ноября 2024
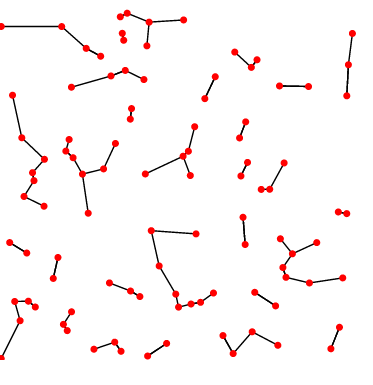
Граф ближайших соседей (Nearest neighbor graph) для множества P, состоящего из n объектов в метрическом пространстве (например, для множества точек на плоскости с евклидовой метрикой) — это ориентированный граф, вершинами которого служат элементы множества P, в котором существует дуга из p в q, если q является ближайшим соседом p (т.е. расстояние от p до q не больше, чем от p до любого другого объекта из P).
Во многих обсуждениях направление рёбер игнорируется и граф ближайших соседей определяется как обычный (неориентированный) граф. Однако отношение ближайшего соседства не является симметричным, т. е. если q является ближайшим соседом p, то p не обязательно будет ближайшим соседом q.