Сеть Петри: различия между версиями
KVN (обсуждение | вклад) |
KVN (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
Сеть Петри ([[Petri net|''Petri net'']]) —– одна из наиболее популярных моделей параллельных систем, используемая как для теоретических исследований, так и практических применений в различных областях. Она используется для моделирования распределенных баз данных и операционных систем, архитектур вычислительных машин, систем и сетей, систем программного обеспечения, протоколов коммуникаций, семантики параллельных языков, систем с элементами искусственного интеллекта и т. д. | |||
для | |||
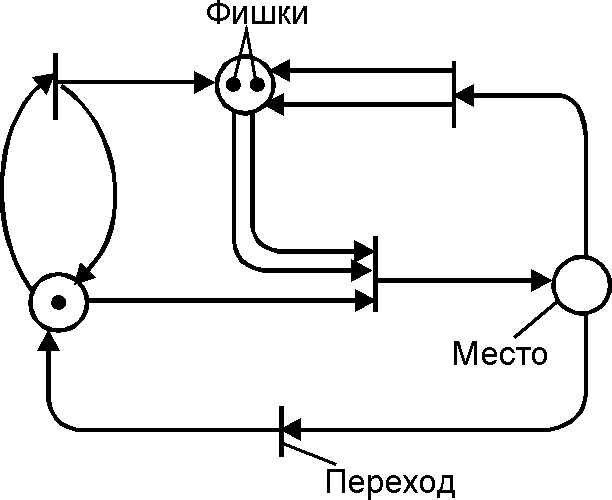
[[Файл:Petri net.png|350px|right]] | Сети Петри ориентированы на моделирование «неалгоритмических» параллельных систем в виде причинно–следственных связей между событиями их недетерминированного поведения на основе [[Сеть|''сети'']] с двумя типами вершин: места и переходы. Каждый переход связывается с соответствующим множеством входных мест и соответствующим множеством выходных мест. Обычно вершины-места изображаются кружками, а вершины-переходы — барьерами (а также прямоугольниками или квадратами, если переходы являются неэлементарными объектами). Каждый переход соединяется с каждым из входных мест дугой, идущей из вершины-места к переходу, и с каждым выходным местом — дугой, направленной от перехода к вершине-месту.[[Файл:Petri net.png|350px|right]] | ||
Состояние параллельной системы представляется наличием определенных | Состояние параллельной системы представляется наличием определенных меток у вершин, а конкретное состояние отображается конкретной конфигурацией меток. Такое распределение меток между местами называется ''разметкой,'' которая обычно изображается в виде черных точек (фишек) внутри соответствующих кружков. | ||
конфигурацией меток. Такое распределение меток между местами | Функционирование сети Петри описывается формально с помощью множества последовательностей срабатываний переходов, меняющих разметки, и множества достижимых в сети разметок. Эти понятия определяются через правила срабатывания переходов сети. | ||
называется ''разметкой'' | |||
Переход может срабатывать (отображая смену состояния) только тогда, когда | Переход может срабатывать (отображая смену состояния) только тогда, когда | ||
Версия от 15:14, 29 октября 2024
Сеть Петри (Petri net) —– одна из наиболее популярных моделей параллельных систем, используемая как для теоретических исследований, так и практических применений в различных областях. Она используется для моделирования распределенных баз данных и операционных систем, архитектур вычислительных машин, систем и сетей, систем программного обеспечения, протоколов коммуникаций, семантики параллельных языков, систем с элементами искусственного интеллекта и т. д.
Сети Петри ориентированы на моделирование «неалгоритмических» параллельных систем в виде причинно–следственных связей между событиями их недетерминированного поведения на основе сети с двумя типами вершин: места и переходы. Каждый переход связывается с соответствующим множеством входных мест и соответствующим множеством выходных мест. Обычно вершины-места изображаются кружками, а вершины-переходы — барьерами (а также прямоугольниками или квадратами, если переходы являются неэлементарными объектами). Каждый переход соединяется с каждым из входных мест дугой, идущей из вершины-места к переходу, и с каждым выходным местом — дугой, направленной от перехода к вершине-месту.
Состояние параллельной системы представляется наличием определенных меток у вершин, а конкретное состояние отображается конкретной конфигурацией меток. Такое распределение меток между местами называется разметкой, которая обычно изображается в виде черных точек (фишек) внутри соответствующих кружков.
Функционирование сети Петри описывается формально с помощью множества последовательностей срабатываний переходов, меняющих разметки, и множества достижимых в сети разметок. Эти понятия определяются через правила срабатывания переходов сети.
Переход может срабатывать (отображая смену состояния) только тогда, когда каждое из его входных мест имеет по меньшей мере одну метку (фишку). Когда переход срабатывает, происходит изъятие метки из каждого его входного места и пересылка по одной метке в каждое из его выходных мест. Таким образом, комбинация входных и выходных мест некоторого перехода отображает как условия, при которых может произойти изменение состояния, так и влияние этого изменения.
Срабатывание перехода — это неделимое событие, и потому одновременное срабатывание двух или более переходов невозможно. Когда состояние таково, что два или более переходов претендуют на срабатывание, каждый из них должен рассматриваться отдельно.
Начиная с начальной разметки, которая соответствует исходному (начальному) состоянию системы, и выполняя очевидную процедуру генерирования другой разметки, достижимой из текущей за счет срабатывания некоторого перехода, можно исследовать возможные состояния системы и пути их достижения. Например, могут быть легко обнаружены тупиковые состояния и непродуктивные зацикливания и вообще всегда можно установить, соответствует ли поведение системы ожидаемому. Хотя процедура генерации достижимой разметки довольно тривиальна, попытки исчерпывающего анализа поведения системы таким способом оказываются тщетными часто из-за уже одного только числа разметок, которое может быть бесконечным. Таким образом, главная задача, состоящая в определении достижимости данной разметки из заданного исходного состояния, пока не поддается решению. Неоднократные попытки доказать общепринятую гипотезу о разрешимости последней, страдали одним общим недостатком — в доказательствах были обнаружены ошибки. Вместе с тем многие другие проблемы сетей Петри эквивалентны ей в том смысле, что их разрешимость или неразрешимость непосредственно следует из разрешимости или неразрешимости проблемы достижимости.
Сеть Петри была изобретена в ФРГ в начале 60-х годов А.А.Петри.
Литература
- Котов В.Е. Сети Петри. — М.: Наука, 1984.
- Толковый словарь по вычислительным системам. — М.: Машиностроение,1991.
- Касьянов В.Н., Касьянова Е.В. Теория вычислений. — Новосибирск: ИНЦ НГУ, 2018.