Циклический участок: различия между версиями
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Циклический участок''' (''[[Loop region]]'') | '''Циклический участок''' (''[[Loop region]]'') — конструкция, позволяющая на основе анализа ''[[уграф|уграфа]]'' с <math>\,n</math> [[вершина|вершинами]] и <math>\,m</math> [[дуга|дугами]] за время <math>\,O(nm)</math> выявлять циклическую структуру [[алгоритм|алгоритма]] и находить отношения частот выполнения между всеми подмножествами его элементов, которые | ||
конструкция, позволяющая на основе анализа ''[[уграф|уграфа]]'' с | не противоречат ''достоверным отношениям частот выполнения'', если уграф <math>\,G</math> алгоритма является ''[[регуляризуемый граф|регуляризуемым]]''. | ||
<math>n</math> [[вершина|вершинами]] и <math>m</math> [[дуга|дугами]] за время <math>O(nm)</math> выявлять циклическую структуру [[алгоритм|алгоритма]] и находить отношения частот | |||
выполнения между всеми подмножествами его элементов, которые | |||
не противоречат ''достоверным отношениям частот выполнения'', если уграф <math>G</math> алгоритма является ''[[регуляризуемый граф|регуляризуемым]]''. | |||
Пусть <math>G_0=G, G_1, \ldots, G_r</math> | Пусть <math>G_0=G, G_1, \ldots, G_r</math> — такая последовательность уграфов, в которой только <math>\,G_r</math> не содержит нетривиальных ''[[бикомпонента|бикомпонент]]'', и для любого <math>\,i</math> уграф <math>\,G_i</math> получается из <math>\,G_{i-1}</math> удалением в каждой нетривиальной бикомпоненте <math>\,C</math> уграфа <math>\,G_{i-1}</math> всех дуг, заходящих в один из ее ''[[вход|входов]]''. Эту ''[[входная вершина подграфа|входную вершину]]'' бикомпоненты <math>\,C</math> называют ее ''[[голова|головой]]'', а удаленные дуги — ''[[дуга повторения уровня i|дугами повторения уровня <math>\,i</math>]]''. | ||
уграфов, в которой только <math>G_r</math> не содержит нетривиальных | Пусть <math>\,I_i</math> обозначает множество всех дуг повторения уровня <math>\,i.</math> Части схемы <math>\,G,</math> называемые ее '''циклическими участками''', определяются по следующим двум правилам: | ||
''[[бикомпонента|бикомпонент]]'', и для любого <math>i</math> уграф <math>G_i</math> получается | |||
из <math>G_{i-1}</math> удалением в каждой нетривиальной бикомпоненте | |||
<math>C</math> уграфа <math>G_{i-1}</math> всех дуг, заходящих в один из ее | |||
''[[вход|входов]]''. Эту ''[[входная вершина подграфа|входную вершину]]'' бикомпоненты <math>C</math> называют ее ''[[голова|головой]]'', а удаленные дуги | |||
Пусть <math>I_i</math> обозначает множество | |||
всех дуг повторения уровня <math>i</math> | |||
Части схемы <math>G</math> | |||
'''циклическими участками''', | |||
определяются по следующим двум правилам: | |||
1) '''Циклический участок''' нулевого уровня в уграфе <math>G</math> один; он состоит | 1) '''Циклический участок''' нулевого уровня в уграфе <math>\,G</math> один; он состоит | ||
из всех тех вершин и дуг, которые принадлежат [[путь|путям]] по <math>G_r</math> | из всех тех вершин и дуг, которые принадлежат [[путь|путям]] по <math>\,G_r</math> | ||
от <math>p_0</math> к <math>q_0</math>, и имеет ''головой'' вершину <math>p_0</math>; | от <math>\,p_0</math> к <math>\,q_0</math>, и имеет ''головой'' вершину <math>\,p_0</math>; | ||
2) пусть для некоторого <math>i | 2) пусть для некоторого <math>i,\,i>0,\,C</math> — бикомпонента схемы <math>\,G_{i-1}</math> с головой <math>\,p,</math> тогда в <math>\,G</math> имеется циклический участок уровня <math>\,i</math> с головой <math>\,p;</math> он состоит из всех тех вершин и дуг, из которых достижима <math>\,p</math> в графе, полученном из <math>\,C</math> удалением всех дуг повторения уровня <math>\,j>i.</math> | ||
<math>G_{i-1}</math> с головой <math>p</math> | |||
участок уровня <math>i</math> с головой <math>p</math> | |||
вершин и дуг, из которых достижима <math>p</math> в графе, полученном | |||
из <math>C</math> удалением всех дуг повторения уровня <math>j>i</math> | |||
[[Файл:Loop region.gif| | [[Файл:Loop region.gif|700px]] | ||
==См. также == | ==См. также == | ||
''[[Участок повторяемости]].'' | * ''[[Участок повторяемости]].'' | ||
==Литература== | ==Литература== | ||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
Текущая версия от 05:36, 30 сентября 2011
Циклический участок (Loop region) — конструкция, позволяющая на основе анализа уграфа с [math]\displaystyle{ \,n }[/math] вершинами и [math]\displaystyle{ \,m }[/math] дугами за время [math]\displaystyle{ \,O(nm) }[/math] выявлять циклическую структуру алгоритма и находить отношения частот выполнения между всеми подмножествами его элементов, которые не противоречат достоверным отношениям частот выполнения, если уграф [math]\displaystyle{ \,G }[/math] алгоритма является регуляризуемым.
Пусть [math]\displaystyle{ G_0=G, G_1, \ldots, G_r }[/math] — такая последовательность уграфов, в которой только [math]\displaystyle{ \,G_r }[/math] не содержит нетривиальных бикомпонент, и для любого [math]\displaystyle{ \,i }[/math] уграф [math]\displaystyle{ \,G_i }[/math] получается из [math]\displaystyle{ \,G_{i-1} }[/math] удалением в каждой нетривиальной бикомпоненте [math]\displaystyle{ \,C }[/math] уграфа [math]\displaystyle{ \,G_{i-1} }[/math] всех дуг, заходящих в один из ее входов. Эту входную вершину бикомпоненты [math]\displaystyle{ \,C }[/math] называют ее головой, а удаленные дуги — дугами повторения уровня [math]\displaystyle{ \,i }[/math]. Пусть [math]\displaystyle{ \,I_i }[/math] обозначает множество всех дуг повторения уровня [math]\displaystyle{ \,i. }[/math] Части схемы [math]\displaystyle{ \,G, }[/math] называемые ее циклическими участками, определяются по следующим двум правилам:
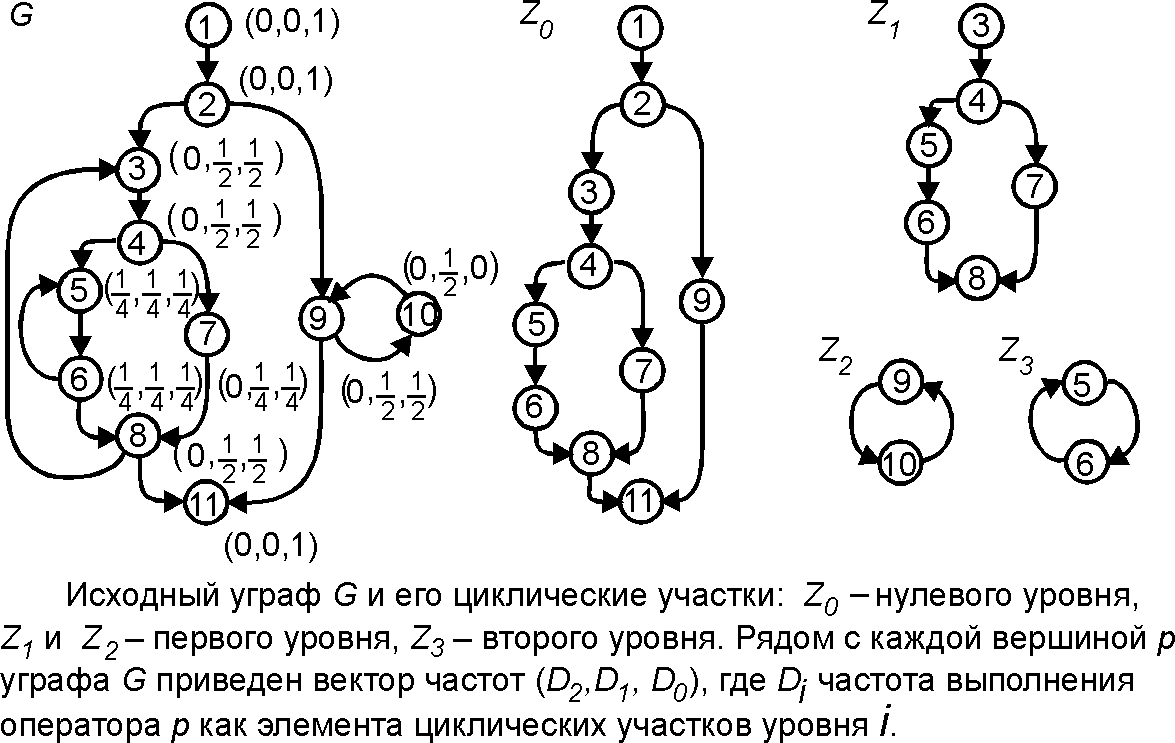
1) Циклический участок нулевого уровня в уграфе [math]\displaystyle{ \,G }[/math] один; он состоит из всех тех вершин и дуг, которые принадлежат путям по [math]\displaystyle{ \,G_r }[/math] от [math]\displaystyle{ \,p_0 }[/math] к [math]\displaystyle{ \,q_0 }[/math], и имеет головой вершину [math]\displaystyle{ \,p_0 }[/math];
2) пусть для некоторого [math]\displaystyle{ i,\,i\gt 0,\,C }[/math] — бикомпонента схемы [math]\displaystyle{ \,G_{i-1} }[/math] с головой [math]\displaystyle{ \,p, }[/math] тогда в [math]\displaystyle{ \,G }[/math] имеется циклический участок уровня [math]\displaystyle{ \,i }[/math] с головой [math]\displaystyle{ \,p; }[/math] он состоит из всех тех вершин и дуг, из которых достижима [math]\displaystyle{ \,p }[/math] в графе, полученном из [math]\displaystyle{ \,C }[/math] удалением всех дуг повторения уровня [math]\displaystyle{ \,j\gt i. }[/math]
См. также
Литература
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.