Складной граф: различия между версиями
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Складной граф''' (''[[Collapsible graph]]'') | '''Складной граф''' (''[[Collapsible graph]]'') — | ||
''[[орграф]]'', который может быть преобразован в [[тривиальный граф|тривиальный]] | ''[[орграф]]'', который может быть преобразован в [[тривиальный граф|тривиальный]] | ||
некоторой последовательностью следующих трансформаций: | некоторой последовательностью следующих трансформаций: | ||
[[Файл:Collapsible | [[Файл:Collapsible graph2.png|500px]] | ||
(1) удаление [[дуга|дуги]] <math>(x,y)</math> и вершины <math>y</math>, если | (1) удаление [[дуга|дуги]] <math>(x,y)</math> и вершины <math>y</math>, если | ||
<math>y</math> | <math>y</math> — [[висячая вершина]] с одной [[заходящая дуга|заходящей дугой]]; | ||
(2) замена дуг <math>(x,y)</math>, <math>(y,z)</math> | (2) замена дуг <math>(x,y)</math>, <math>(y,z)</math> | ||
и вершины <math>q</math> на новую дугу <math>(x,z)</math>, если | и вершины <math>q</math> на новую дугу <math>(x,z)</math>, если | ||
<math>y</math> | <math>y</math> — [[вершина]] с одной заходящей дугой и одной [[исходящая дуга|исходящей]]; | ||
(3) удаление одной из двух [[кратные дуги|кратных дуг]]. | (3) удаление одной из двух [[кратные дуги|кратных дуг]]. | ||
| Строка 18: | Строка 18: | ||
Риорданом и Шенноном. Одна трансформация 1 определяет ''[[дерево|деревья]]''. | Риорданом и Шенноном. Одна трансформация 1 определяет ''[[дерево|деревья]]''. | ||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Базисные алгоритмы обработки бесконтурных графов. — Новосибирск: ИСИ СО РАН, 1995. | |||
Текущая версия от 05:13, 8 сентября 2011
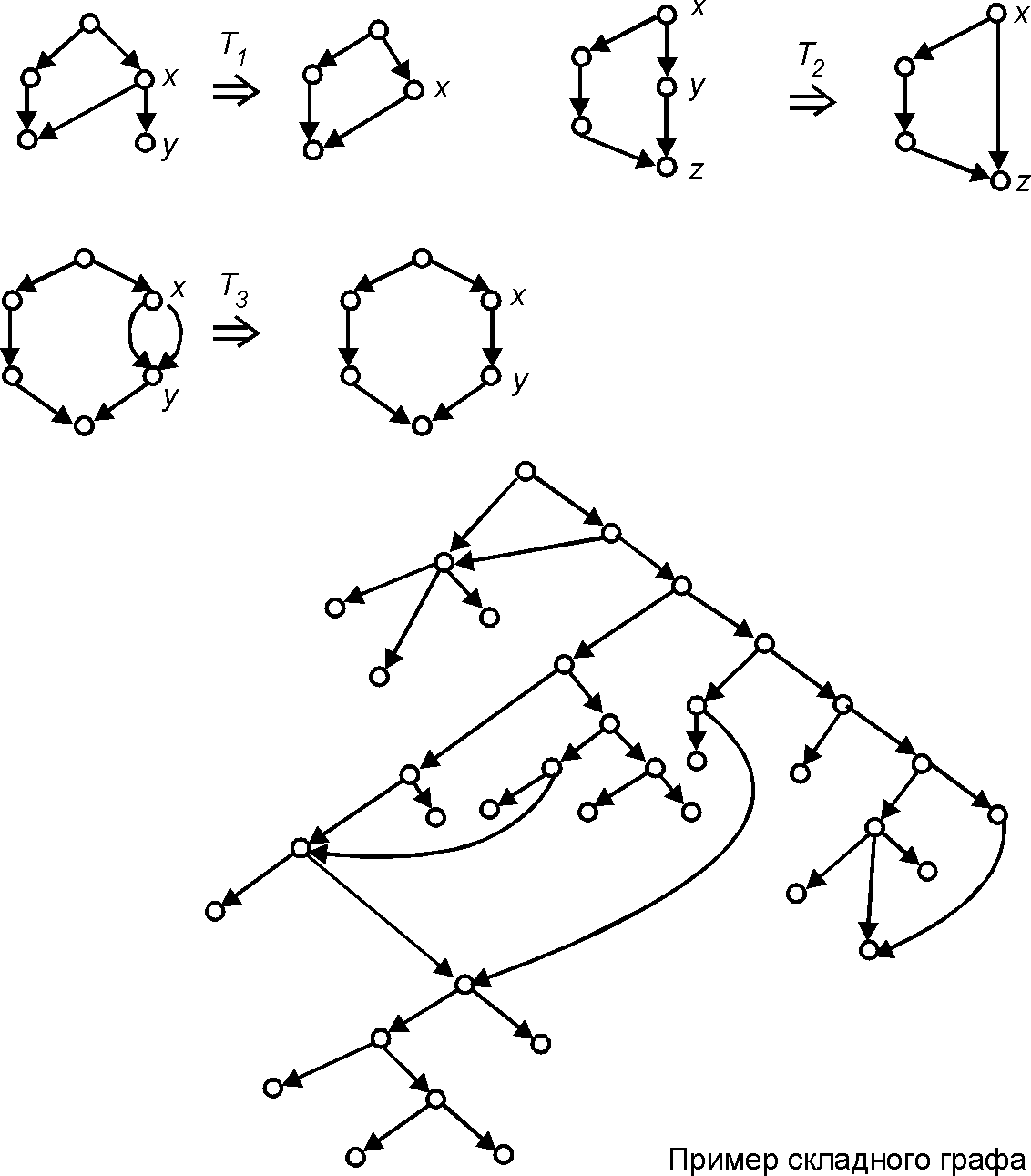
Складной граф (Collapsible graph) — орграф, который может быть преобразован в тривиальный некоторой последовательностью следующих трансформаций:
(1) удаление дуги [math]\displaystyle{ (x,y) }[/math] и вершины [math]\displaystyle{ y }[/math], если [math]\displaystyle{ y }[/math] — висячая вершина с одной заходящей дугой;
(2) замена дуг [math]\displaystyle{ (x,y) }[/math], [math]\displaystyle{ (y,z) }[/math] и вершины [math]\displaystyle{ q }[/math] на новую дугу [math]\displaystyle{ (x,z) }[/math], если [math]\displaystyle{ y }[/math] — вершина с одной заходящей дугой и одной исходящей;
(3) удаление одной из двух кратных дуг.
Без трансформации 1 получаем определение последовательно-параллельных графов, введенных Риорданом и Шенноном. Одна трансформация 1 определяет деревья.
Литература
- Евстигнеев В.А., Касьянов В.Н. Базисные алгоритмы обработки бесконтурных графов. — Новосибирск: ИСИ СО РАН, 1995.