Схемы Янова: различия между версиями
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Схемы Янова''' (''[[Yanov schemata]]'') | '''Схемы Янова''' (''[[Yanov schemata]]'') — | ||
''[[схема программ|схемы программ]]'', которые | ''[[схема программ|схемы программ]]'', которые | ||
были введены в литературу А.А.Ляпуновым и Ю.И.Яновым в 1958 г. | были введены в литературу А.А.Ляпуновым и Ю.И.Яновым в 1958 г. | ||
и направлены на разработку общей теории условий, управляющих | и направлены на разработку общей теории условий, управляющих | ||
последовательностью выполнений операторов в программе. | последовательностью выполнений операторов в программе. | ||
[[Файл:Yanov schemata.gif|600px|right]] | |||
В отличие от ''[[схемы Мартынюка]]'' '''Схемы Янова''' | В отличие от ''[[схемы Мартынюка]]'' '''Схемы Янова''' | ||
содержит | содержит | ||
помимо одной переменной (скажем, <math>x</math>), имеющейся в схеме | помимо одной переменной (скажем, <math>\,x</math>), имеющейся в схеме | ||
Мартынюка, множество специальных логических переменных <math>p_1, | Мартынюка, множество специальных логических переменных <math>p_1, | ||
p_2,\ldots,p_k</math>, управляющих вычислениями, и состоит из | p_2,\ldots,p_k</math>, управляющих вычислениями, и состоит из | ||
| Строка 23: | Строка 25: | ||
Для '''Схем Янова''' проблема эквивалентности разрешима и построена | Для '''Схем Янова''' проблема эквивалентности разрешима и построена | ||
''полная система эквивалентных преобразований'' | ''полная система эквивалентных преобразований'' — система | ||
преобразований, сохраняющих эквивалентность, полная в том | преобразований, сохраняющих эквивалентность, полная в том | ||
смысле, что любую пару эквивалентных схем можно | смысле, что любую пару эквивалентных схем можно | ||
| Строка 30: | Строка 32: | ||
==См. также == | ==См. также == | ||
''[[Неинтерпретированные схемы]], [[Стандартные схемы]], [[Схемы Лаврова]], [[Схема программ]], | * ''[[Неинтерпретированные схемы]],'' | ||
[[Схема с косвенной адресацией]].'' | * ''[[Стандартные схемы]],'' | ||
* ''[[Схемы Лаврова]],'' | |||
* ''[[Схема программ]],'' | |||
* ''[[Схема с косвенной адресацией]].'' | |||
==Литература== | ==Литература== | ||
* Ершов А.П. Введение в теоретическое программирование. Беседы о методе. — М.: Наука, 1977. | |||
* Ершов А.П. Избранные труды. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
Текущая версия от 04:47, 13 сентября 2011
Схемы Янова (Yanov schemata) — схемы программ, которые были введены в литературу А.А.Ляпуновым и Ю.И.Яновым в 1958 г. и направлены на разработку общей теории условий, управляющих последовательностью выполнений операторов в программе.
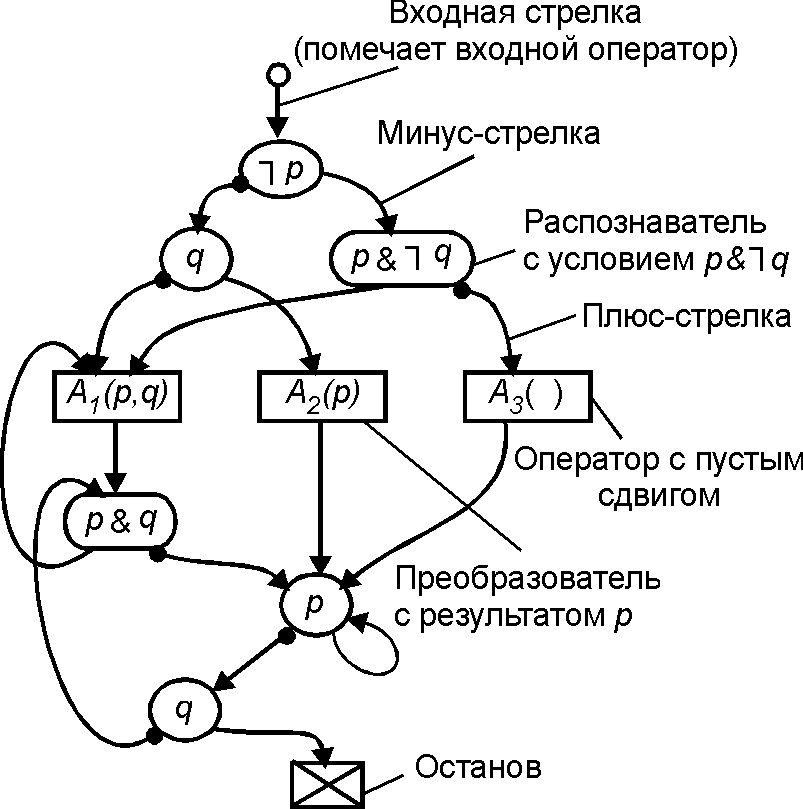
В отличие от схемы Мартынюка Схемы Янова содержит помимо одной переменной (скажем, [math]\displaystyle{ \,x }[/math]), имеющейся в схеме Мартынюка, множество специальных логических переменных [math]\displaystyle{ p_1, p_2,\ldots,p_k }[/math], управляющих вычислениями, и состоит из преобразователей, каждый из которых помимо обязательного аргумента и необязательного результата [math]\displaystyle{ x }[/math] имеет произвольное подмножество логических переменных в качестве результатов, и распознавателей, каждый из которых имеет ровно две исходящие дуги и состоит из слова выбора, имеющего вид произвольной логической функции от переменных [math]\displaystyle{ p_1, p_2,\ldots,p_k }[/math]. Множество логических переменных, являющихся результатами оператора-преобразователя, называется его сдвигом. Дуги, исходящие из распознавателя, различаются и называются соответственно плюс-стрелкой и минус-стрелкой.
Для Схем Янова проблема эквивалентности разрешима и построена полная система эквивалентных преобразований — система преобразований, сохраняющих эквивалентность, полная в том смысле, что любую пару эквивалентных схем можно трансформировать друг в друга последовательным применением этих преобразований.
См. также
- Неинтерпретированные схемы,
- Стандартные схемы,
- Схемы Лаврова,
- Схема программ,
- Схема с косвенной адресацией.
Литература
- Ершов А.П. Введение в теоретическое программирование. Беседы о методе. — М.: Наука, 1977.
- Ершов А.П. Избранные труды. — Новосибирск: Наука. Сиб. отд-ние, 1994.