Дерево вывода: различия между версиями
KEV (обсуждение | вклад) Нет описания правки |
KVN (обсуждение | вклад) Нет описания правки |
||
| (не показано 7 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
'''Дерево вывода''' (''[[Derivation tree | '''Дерево вывода''' (''[[Derivation tree]]'') — способ представления множества ''выводов'' одной и той же ''[[цепочка|цепочки]]'' в ''[[контекстно-свободная грамматика|контекстно-свободной грамматике]]'', различающихся лишь порядком применения правил. | ||
[[Файл:Derivation tree.png| | [[Файл:Derivation tree.png|750px]] | ||
[[Помеченный граф|Помеченное]] [[упорядоченный граф|упорядоченное]] [[дерево]] <math>D</math> | [[Помеченный граф|Помеченное]] [[упорядоченный граф|упорядоченное]] [[дерево]] <math>D</math> | ||
| Строка 8: | Строка 8: | ||
(1) [[корень]] дерева <math>D</math> помечен символом <math>A</math>; | (1) [[корень]] дерева <math>D</math> помечен символом <math>A</math>; | ||
(2) если <math>D_1,\ldots,D_k</math> | (2) если <math>D_1,\ldots,D_k</math> — [[поддерево|поддеревья]], корнями которых являются [[сын|сыновья]] корня <math>D</math>, помеченные символами <math>X_1, \ldots, X_k</math> соответственно, | ||
то <math>A\longrightarrow X_i\ldots X_k</math> --- правило из множества <math>P</math>. Каждое <math>D_i</math> должно либо быть деревом вывода в [[грамматика|грамматике]] <math>G(X_i)=(N,\Sigma,P,X_i)</math>, если <math>X_i</math> - нетерминал, либо состоять из единственной вершины, помеченной символом <math>X_i</math>, если <math>X_i</math> | то <math>A\longrightarrow X_i\ldots X_k</math> --- правило из множества <math>P</math>. Каждое <math>D_i</math> должно либо быть деревом вывода в [[грамматика|грамматике]] <math>G(X_i)=(N,\Sigma,P,X_i)</math>, если <math>X_i</math> - нетерминал, либо состоять из единственной вершины, помеченной символом <math>X_i</math>, если <math>X_i</math> — [[терминал]]; | ||
(3) если корень дерева имеет единственного сына, помеченного <math>e</math>, то этот сын образует дерево, состоящее из единственной вершины, и <math>A\longrightarrow e</math> | (3) если корень дерева имеет единственного сына, помеченного <math>e</math>, то этот сын образует дерево, состоящее из единственной вершины, и <math>A\longrightarrow e</math> — правило из | ||
множества <math>P</math>. | множества <math>P</math>. | ||
| Строка 23: | Строка 23: | ||
''[[Крона сечения]]'' дерева <math>D</math> определяется как [[цепочка]], которая получается конкатенацией меток вершин, образующих данное сечение, в их упорядочении слева направо, определяемом по следующему правилу. Рассматривается имеющееся упорядочение на множестве сыновей <math>p_1,</math> <math> \ldots,</math> <math>p_k</math> каждого [[отец вершины ордерева|отца]] <math>p</math> в дереве <math>D</math> и считается, что для любых <math>i<j</math> вершина <math>p_i</math> и все ее [[потомок вершины|потомки]] расположены левее вершины <math>p_j</math> и всех ее потомков. | ''[[Крона сечения]]'' дерева <math>D</math> определяется как [[цепочка]], которая получается конкатенацией меток вершин, образующих данное сечение, в их упорядочении слева направо, определяемом по следующему правилу. Рассматривается имеющееся упорядочение на множестве сыновей <math>p_1,</math> <math> \ldots,</math> <math>p_k</math> каждого [[отец вершины ордерева|отца]] <math>p</math> в дереве <math>D</math> и считается, что для любых <math>i<j</math> вершина <math>p_i</math> и все ее [[потомок вершины|потомки]] расположены левее вершины <math>p_j</math> и всех ее потомков. | ||
''[[Кроной дерева]]'' <math>D</math> называется крона сечения, образованного из [[лист|листьев]] дерева <math>D</math>. | ''[[Крона дерева|Кроной дерева]]'' <math>D</math> называется крона сечения, образованного из [[лист|листьев]] дерева <math>D</math>. | ||
Другие названия | Другие названия — ''[[Дерево разбора]], [[Синтаксическое дерево]].'' | ||
==См. также== | ==См. также== | ||
''[[Абстрактное синтаксическое представление]].'' | * ''[[(Абстрактное) синтаксическое представление|Абстрактное синтаксическое представление]].'' | ||
==Литература== | ==Литература== | ||
* Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. — М.: Мир, 1978. — Т. 1,2. | |||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
* Касьянов В.Н. Лекции по теории формальных языков, автоматов и сложности вычислений. — Новосибирск: НГУ, 1995. | |||
* Касьянов В.Н., Поттосин И.В. Методы построения трансляторов. — Новосибирск: Наука. Сиб. отд-ние, 1986. | |||
[ | [[Категория:Теория формальных языков]] | ||
[[Категория:Синтаксические деревья]] | |||
[ | [[Категория:Основные термины]] | ||
Текущая версия от 13:23, 11 ноября 2024
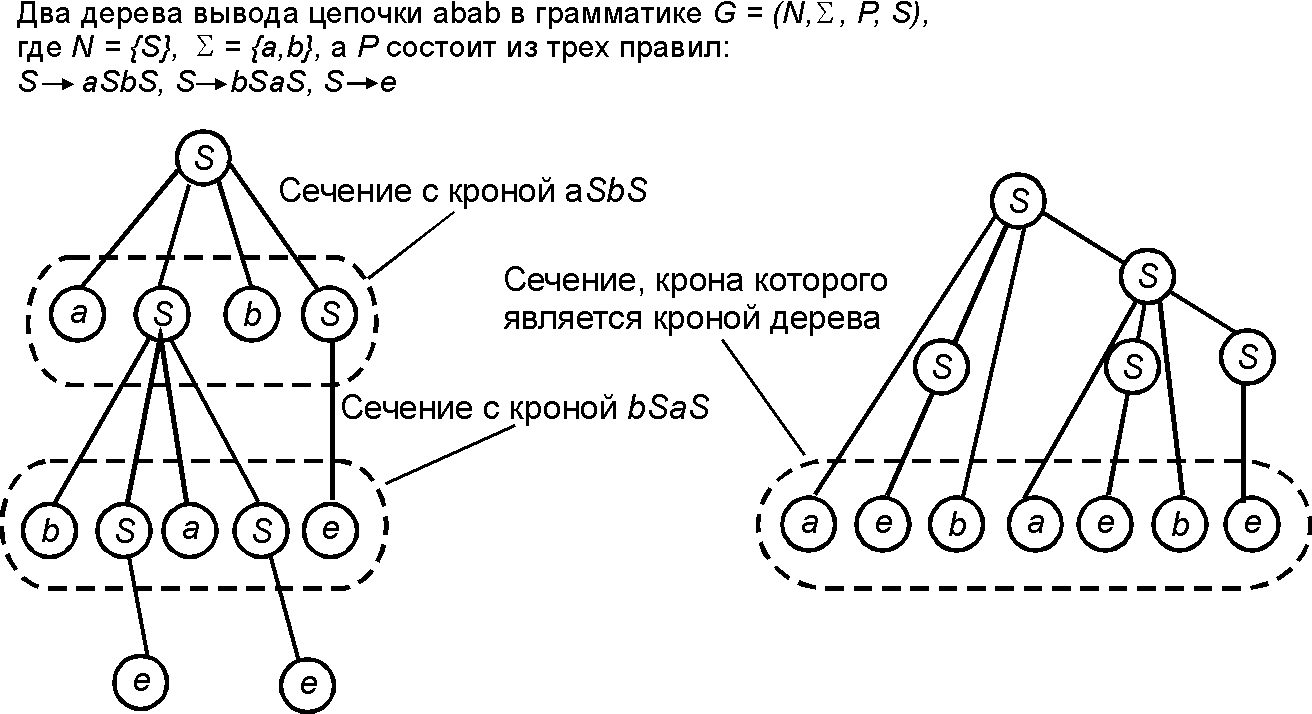
Дерево вывода (Derivation tree) — способ представления множества выводов одной и той же цепочки в контекстно-свободной грамматике, различающихся лишь порядком применения правил.
Помеченное упорядоченное дерево [math]\displaystyle{ D }[/math] называется деревом вывода в контекстно-свободной грамматике [math]\displaystyle{ G(A)=(N,\Sigma,P,A) }[/math], если выполнены следующие условия:
(1) корень дерева [math]\displaystyle{ D }[/math] помечен символом [math]\displaystyle{ A }[/math];
(2) если [math]\displaystyle{ D_1,\ldots,D_k }[/math] — поддеревья, корнями которых являются сыновья корня [math]\displaystyle{ D }[/math], помеченные символами [math]\displaystyle{ X_1, \ldots, X_k }[/math] соответственно, то [math]\displaystyle{ A\longrightarrow X_i\ldots X_k }[/math] --- правило из множества [math]\displaystyle{ P }[/math]. Каждое [math]\displaystyle{ D_i }[/math] должно либо быть деревом вывода в грамматике [math]\displaystyle{ G(X_i)=(N,\Sigma,P,X_i) }[/math], если [math]\displaystyle{ X_i }[/math] - нетерминал, либо состоять из единственной вершины, помеченной символом [math]\displaystyle{ X_i }[/math], если [math]\displaystyle{ X_i }[/math] — терминал;
(3) если корень дерева имеет единственного сына, помеченного [math]\displaystyle{ e }[/math], то этот сын образует дерево, состоящее из единственной вершины, и [math]\displaystyle{ A\longrightarrow e }[/math] — правило из множества [math]\displaystyle{ P }[/math].
Сечением дерева [math]\displaystyle{ D }[/math] называется такое множество [math]\displaystyle{ C }[/math] вершин дерева [math]\displaystyle{ D }[/math], что
(1) никакие две вершины из [math]\displaystyle{ C }[/math] не лежат на одном пути в [math]\displaystyle{ D }[/math],
(2) ни одну вершину дерева [math]\displaystyle{ D }[/math] нельзя добавить к [math]\displaystyle{ C }[/math], не нарушив свойства 1.
Крона сечения дерева [math]\displaystyle{ D }[/math] определяется как цепочка, которая получается конкатенацией меток вершин, образующих данное сечение, в их упорядочении слева направо, определяемом по следующему правилу. Рассматривается имеющееся упорядочение на множестве сыновей [math]\displaystyle{ p_1, }[/math] [math]\displaystyle{ \ldots, }[/math] [math]\displaystyle{ p_k }[/math] каждого отца [math]\displaystyle{ p }[/math] в дереве [math]\displaystyle{ D }[/math] и считается, что для любых [math]\displaystyle{ i\lt j }[/math] вершина [math]\displaystyle{ p_i }[/math] и все ее потомки расположены левее вершины [math]\displaystyle{ p_j }[/math] и всех ее потомков.
Кроной дерева [math]\displaystyle{ D }[/math] называется крона сечения, образованного из листьев дерева [math]\displaystyle{ D }[/math].
Другие названия — Дерево разбора, Синтаксическое дерево.
См. также
Литература
- Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. — М.: Мир, 1978. — Т. 1,2.
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Касьянов В.Н. Лекции по теории формальных языков, автоматов и сложности вычислений. — Новосибирск: НГУ, 1995.
- Касьянов В.Н., Поттосин И.В. Методы построения трансляторов. — Новосибирск: Наука. Сиб. отд-ние, 1986.