2-3-Дерево: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''2-3-Дерево''' (''2-3-Tree'') - выровненное дерево, каждая вершина которого имеет дв...) |
KVN (обсуждение | вклад) |
||
| (не показаны 4 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
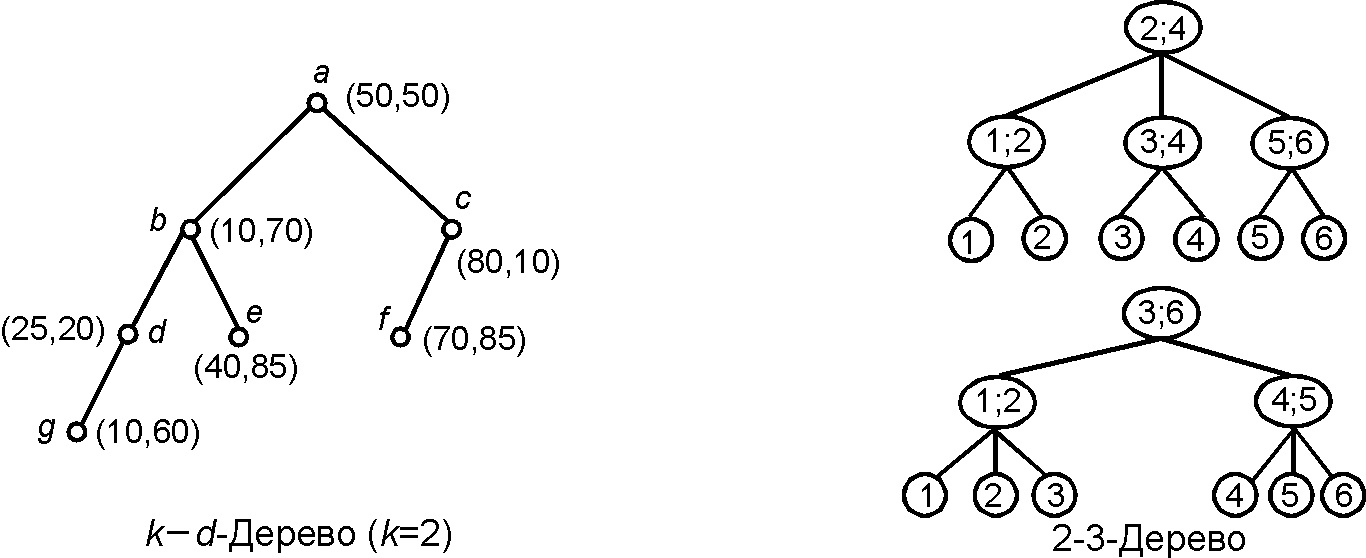
'''2-3-Дерево''' (''2-3-Tree'') | '''2-3-Дерево''' (''[[2-3-Tree]]'') — [[выровненное дерево]], каждая [[вершина]] которого имеет двух или трех [[потомок вершины|потомков]]. Информация в таких [[дерево|деревьях]] хранится в [[лист|листьях]], а остальные вершины содержат вспомогательную информацию для организации поиска. | ||
выровненное дерево, каждая вершина которого имеет двух или трех | |||
потомков. Информация в таких деревьях хранится в листьях, а остальные | [[Файл:2-3-Tree.png|700px]] | ||
вершины содержат вспомогательную информацию для организации поиска. | |||
==Литература== | ==Литература== | ||
* Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. — М.: Мир, 1979. | |||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
[ | [[Категория:Деревья]] | ||
[[Категория:Информационные деревья]] | |||
[[Категория:Основные термины]] | |||
Текущая версия от 15:02, 19 ноября 2024
2-3-Дерево (2-3-Tree) — выровненное дерево, каждая вершина которого имеет двух или трех потомков. Информация в таких деревьях хранится в листьях, а остальные вершины содержат вспомогательную информацию для организации поиска.
Литература
- Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. — М.: Мир, 1979.
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.