Грань: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''Грань''' (''Face, facet'') - для ''плоского графа'' максимальное по включению множес...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Грань''' (''Face, facet'') | [[Файл:Face.png|300px|right]] | ||
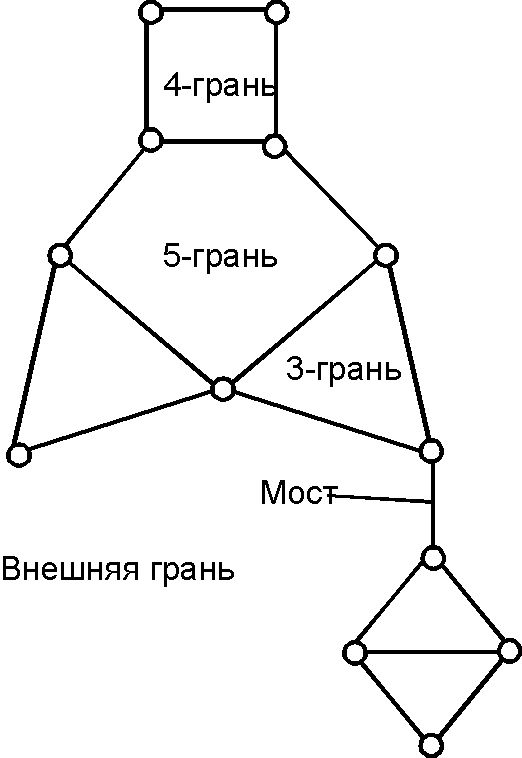
для ''плоского графа'' максимальное по включению | '''Грань''' (''[[Face]], [[facet]]'') — для [[плоский граф|''плоского графа'']] максимальное по включению множество точек плоскости, каждая пара которых может быть соединена жордановой кривой, не пересекающей [[ребро|ребра]] [[граф|графа]]. Тем самым каждая точка плоскости принадлежит хотя бы одной грани плоского графа. | ||
множество точек плоскости, каждая пара которых может | Всякий плоский граф имеет одну, и притом единственную, неограниченную грань, называемую [[грань внешняя|''внешней гранью'']]; остальные грани называются [[грань внутренняя|''внутренними'']]. | ||
быть соединена жордановой кривой, не пересекающей | |||
ребра графа. Тем самым каждая точка плоскости | |||
принадлежит хотя бы одной грани плоского графа. | |||
Всякий плоский граф имеет одну, и притом | |||
единственную, неограниченную грань, называемую ''внешней гранью''; остальные грани называются | |||
''внутренними''. | |||
==Литература== | ==Литература== | ||
* Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990. | |||
Текущая версия от 05:45, 24 декабря 2010
Грань (Face, facet) — для плоского графа максимальное по включению множество точек плоскости, каждая пара которых может быть соединена жордановой кривой, не пересекающей ребра графа. Тем самым каждая точка плоскости принадлежит хотя бы одной грани плоского графа. Всякий плоский граф имеет одну, и притом единственную, неограниченную грань, называемую внешней гранью; остальные грани называются внутренними.
Литература
- Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.