Евклидово минимальное остовное дерево: различия между версиями
Перейти к навигации
Перейти к поиску
KVN (обсуждение | вклад) (Новая страница: «'''Евклидово минимальное остовное дерево''' (''Euclidean minimum spanning tree, EMST'') — это минимальное остовное дерево множества из <math>n</math> точек на плоскости (или более обще, в <math>\R^d</math>, где <math>d \ge 2</math>), где вес ребра между любой парой точек является евклидовым расс...») |
KVN (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
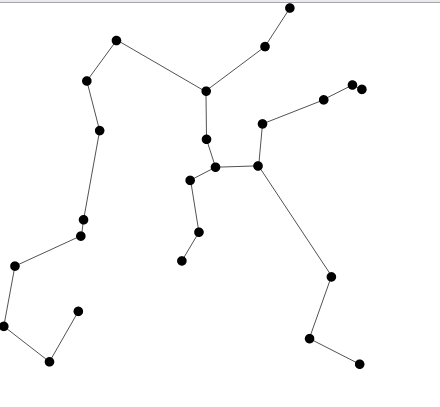
'''Евклидово минимальное остовное дерево''' (''Euclidean minimum spanning tree, EMST'') — это [[минимальное остовное дерево]] множества из <math>n</math> точек на плоскости (или более обще, в <math>\R^d</math>, где <math>d \ge 2</math>), где вес ребра между любой парой точек является евклидовым расстоянием между ними. Другими словами, '''Евклидово минимальное остовное дерево''' соединяет отрезками некоторые пары заданного множества из <math>n</math> точек так, что любая точка множества стала достижимой из любой другой точки множества по этим отрезкам, а общая длина всех отрезков была бы минимальна. | '''Евклидово минимальное остовное дерево''' (''Euclidean minimum spanning tree, EMST'') — это [[минимальное остовное дерево]] множества из <math>n</math> точек на плоскости (или более обще, в <math>\R^d</math>, где <math>d \ge 2</math>), где вес ребра между любой парой точек является евклидовым расстоянием между ними. Другими словами, '''Евклидово минимальное остовное дерево''' соединяет отрезками некоторые пары заданного множества из <math>n</math> точек так, что любая точка множества стала достижимой из любой другой точки множества по этим отрезкам, а общая длина всех отрезков была бы минимальна. | ||
[[Файл: Euclidean_minimum_spanning_tree.png|275px]] | |||
[[Категория: Обыкновенные графы]] | [[Категория: Обыкновенные графы]] | ||
[[Категория:Неориентированные графы]] | |||
Текущая версия от 11:05, 25 ноября 2024
Евклидово минимальное остовное дерево (Euclidean minimum spanning tree, EMST) — это минимальное остовное дерево множества из [math]\displaystyle{ n }[/math] точек на плоскости (или более обще, в [math]\displaystyle{ \R^d }[/math], где [math]\displaystyle{ d \ge 2 }[/math]), где вес ребра между любой парой точек является евклидовым расстоянием между ними. Другими словами, Евклидово минимальное остовное дерево соединяет отрезками некоторые пары заданного множества из [math]\displaystyle{ n }[/math] точек так, что любая точка множества стала достижимой из любой другой точки множества по этим отрезкам, а общая длина всех отрезков была бы минимальна.