Граф Габриэля: различия между версиями
KVN (обсуждение | вклад) (Новая страница: «'''Граф Габриэля''' (''Gabriel graph'') множества <math>S</math> точек двумерного пространства выражает понятие близости этих точек. Формально, это --- граф <math>G</math> с множеством вершин <math>S</math>, в котором любые две различные точки <math>p, q \in S</math> смежны, если замкнутый кр...») |
KVN (обсуждение | вклад) Нет описания правки |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
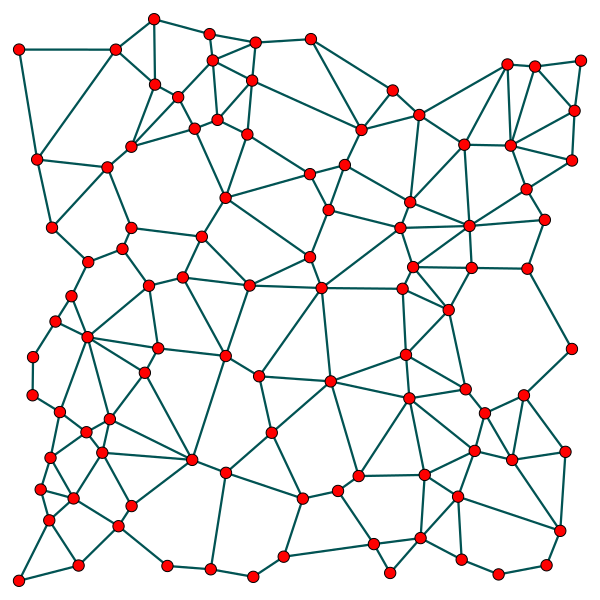
'''Граф Габриэля''' (''Gabriel graph'') множества <math>S</math> точек двумерного пространства выражает понятие близости этих точек. Формально, это --- [[граф]] <math>G</math> с множеством вершин <math>S</math>, в котором любые две различные точки <math>p, q \in S</math> смежны, если замкнутый круг с отрезком <math>\overline{pq}</math> в качестве диаметра не содержит других элементов множества <math>S</math>. | '''Граф Габриэля''' (''Gabriel graph'') множества <math>S</math> точек двумерного пространства выражает понятие близости этих точек. Формально, это --- [[граф]] <math>G</math> с множеством вершин <math>S</math>, в котором любые две различные точки <math>p, q \in S</math> смежны, если замкнутый круг с отрезком <math>\overline{pq}</math> в качестве диаметра не содержит других элементов множества <math>S</math>. | ||
'''Графы Габриэля''' естественным образом обобщаются на пространства более высоких размерностей заменой кругов на шары. Названы в честь К. | '''Графы Габриэля''' естественным образом обобщаются на пространства более высоких размерностей заменой кругов на шары. Названы в честь К.Р.Габриэля (''K.R. Gabriel''), который их ввёл в 1969. | ||
'''Граф Габриэля''' является [[подграф]]ом [[Триангуляция Делоне|триангуляции Делоне]] и может быть найден за линейное время, если триангуляция Делоне задана. Он содержит в качестве [[подграф]]ов [[евклидово минимальное остовное дерево]], [[граф относительных окрестностей]] и [[граф ближайших соседей]]. | '''Граф Габриэля''' является [[подграф]]ом [[Триангуляция Делоне|триангуляции Делоне]] и может быть найден за линейное время, если триангуляция Делоне задана. Он содержит в качестве [[подграф]]ов [[евклидово минимальное остовное дерево]], [[граф относительных окрестностей]] и [[граф ближайших соседей]]. | ||
[[Категория: Обыкновенные графы]] | [[Файл:Gabriel_graph.png|275px]] | ||
[[Категория:Обыкновенные графы]] | |||
[[Категория:Неориентированные графы]] | |||
Текущая версия от 10:58, 25 ноября 2024
Граф Габриэля (Gabriel graph) множества [math]\displaystyle{ S }[/math] точек двумерного пространства выражает понятие близости этих точек. Формально, это --- граф [math]\displaystyle{ G }[/math] с множеством вершин [math]\displaystyle{ S }[/math], в котором любые две различные точки [math]\displaystyle{ p, q \in S }[/math] смежны, если замкнутый круг с отрезком [math]\displaystyle{ \overline{pq} }[/math] в качестве диаметра не содержит других элементов множества [math]\displaystyle{ S }[/math].
Графы Габриэля естественным образом обобщаются на пространства более высоких размерностей заменой кругов на шары. Названы в честь К.Р.Габриэля (K.R. Gabriel), который их ввёл в 1969.
Граф Габриэля является подграфом триангуляции Делоне и может быть найден за линейное время, если триангуляция Делоне задана. Он содержит в качестве подграфов евклидово минимальное остовное дерево, граф относительных окрестностей и граф ближайших соседей.