Расщепление вершины: различия между версиями
Glk (обсуждение | вклад) (Создана новая страница размером '''Расщепление вершины''' (''Vertex splitting'') - 1) преобразование графа, заключающеес...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Расщепление вершины''' (''Vertex splitting'') | '''Расщепление вершины''' (''[[Vertex splitting]]'') — | ||
1) преобразование графа, | 1) преобразование [[граф|графа]], | ||
заключающееся в замене вершины <math>v</math> вершинами | заключающееся в замене [[вершина|вершины]] <math>v</math> вершинами | ||
<math>v'</math> и <math>v''</math>, соединенными ребром <math>(v',v'')</math>, причем вершины, смежные | <math>v'</math> и <math>v''</math>, соединенными [[ребро|ребром]] <math>(v',v'')</math>, причем вершины, [[смежные вершины|смежные]] | ||
с <math>v</math>, распределяются между новыми вершинами каким-то способом. При | с <math>v</math>, распределяются между новыми вершинами каким-то способом. При | ||
расщеплении вершины в орграфе последняя заменяется вершинами <math>v'</math> и | расщеплении вершины в [[орграф|орграфе]] последняя заменяется вершинами <math>v'</math> и | ||
<math>v''</math>, соединенными | <math>v''</math>, соединенными | ||
дугой <math>(v',v'')</math>, причем дуги, заходившие в <math>v</math>, | [[дуга|дугой]] <math>(v',v'')</math>, причем дуги, [[заходящая дуга|заходившие]] в <math>v</math>, | ||
теперь заходят в <math>v'</math>, а дуги, исходившие из <math>v</math>, теперь исходят из | теперь заходят в <math>v'</math>, а дуги, [[исходящая дуга|исходившие]] из <math>v</math>, теперь исходят из | ||
<math>v''</math>; | <math>v''</math>; | ||
2) преобразование '' уграфа'', при котором некоторая вершина | 2) преобразование '' [[уграф|уграфа]]'', при котором некоторая [[вершина]] | ||
<math>p</math>, не являющаяся ни '' начальной'', ни ''конечной'' и не имеющая петли, | <math>p</math>, не являющаяся ни '' [[начальная вершина|начальной]]'', ни ''[[конечная вершина|конечной]]'' и не имеющая [[петля|петли]], | ||
заменяется на <math>r</math> экземпляров по одному для каждой из <math>r</math> | заменяется на <math>r</math> экземпляров по одному для каждой из <math>r</math> | ||
заходящих в <math>p</math> дуг. | заходящих в <math>p</math> дуг. | ||
[[Файл:Vertex splitting.png|400px]] | |||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
* Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990. | |||
Текущая версия от 05:26, 30 августа 2011
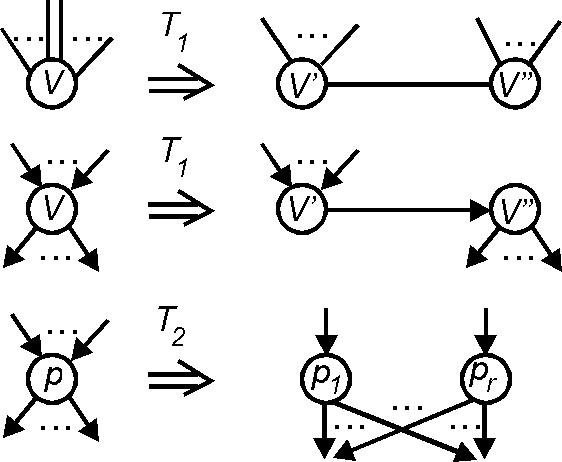
Расщепление вершины (Vertex splitting) — 1) преобразование графа, заключающееся в замене вершины [math]\displaystyle{ v }[/math] вершинами [math]\displaystyle{ v' }[/math] и [math]\displaystyle{ v'' }[/math], соединенными ребром [math]\displaystyle{ (v',v'') }[/math], причем вершины, смежные с [math]\displaystyle{ v }[/math], распределяются между новыми вершинами каким-то способом. При расщеплении вершины в орграфе последняя заменяется вершинами [math]\displaystyle{ v' }[/math] и [math]\displaystyle{ v'' }[/math], соединенными дугой [math]\displaystyle{ (v',v'') }[/math], причем дуги, заходившие в [math]\displaystyle{ v }[/math], теперь заходят в [math]\displaystyle{ v' }[/math], а дуги, исходившие из [math]\displaystyle{ v }[/math], теперь исходят из [math]\displaystyle{ v'' }[/math];
2) преобразование уграфа, при котором некоторая вершина [math]\displaystyle{ p }[/math], не являющаяся ни начальной, ни конечной и не имеющая петли, заменяется на [math]\displaystyle{ r }[/math] экземпляров по одному для каждой из [math]\displaystyle{ r }[/math] заходящих в [math]\displaystyle{ p }[/math] дуг.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.
- Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.