Линейная компонента: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''Линейная компонента''' (''Linear component'') - ''гамак'' </math>C<math> управляющего графа </...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Линейная компонента''' (''Linear component'') | [[Файл:Linear component.png|300px|right]] | ||
''гамак'' < | '''Линейная компонента''' (''[[Linear component]]'') — ''[[гамак]]'' <math>C</math> [[управляющий граф|управляющего графа]] <math>G</math>, обладающий следующими | ||
свойствами: начальная и конечная (если она есть) вершины < | свойствами: [[начальная вершина|начальная]] и [[конечная вершина|конечная]] (если она есть) [[вершина|вершины]] <math>C</math> принадлежат каждому [[путь|пути]] из [[вход|входа]] <math>G</math> в его [[выход]]; из конечной вершины гамака <math>C</math> не [[достижимость|достижима]] в <math>G</math> начальная вершина гамака <math>C</math>; <math>C</math> не | ||
принадлежат каждому пути из входа < | содержит собственного [[подграф|подграфа]], который был бы гамаком и обладал | ||
гамака < | |||
содержит собственного подграфа, который был бы гамаком и обладал | |||
бы первыми двумя свойствами. | бы первыми двумя свойствами. | ||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
Текущая версия от 06:20, 29 апреля 2011
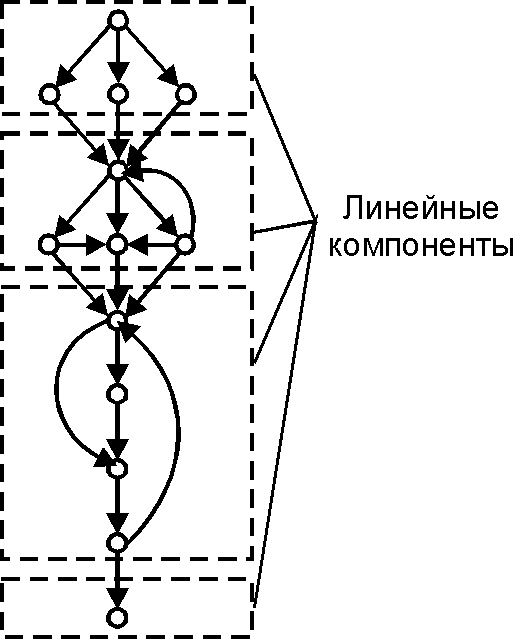
Линейная компонента (Linear component) — гамак [math]\displaystyle{ C }[/math] управляющего графа [math]\displaystyle{ G }[/math], обладающий следующими свойствами: начальная и конечная (если она есть) вершины [math]\displaystyle{ C }[/math] принадлежат каждому пути из входа [math]\displaystyle{ G }[/math] в его выход; из конечной вершины гамака [math]\displaystyle{ C }[/math] не достижима в [math]\displaystyle{ G }[/math] начальная вершина гамака [math]\displaystyle{ C }[/math]; [math]\displaystyle{ C }[/math] не содержит собственного подграфа, который был бы гамаком и обладал бы первыми двумя свойствами.
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.