Двойственный граф: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''Двойственный граф''' (''Dual graph'') - для данного плоского графа (геометрически)...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Двойственный граф''' (''Dual graph'') | '''Двойственный граф''' (''[[Dual graph]]'') — для данного [[плоский граф|плоского графа]] (геометрически) двойственный [[граф]] есть снова плоский граф, [[вершина|вершины]] которого суть грани исходного графа и две [[смежные вершины|вершины смежны]], если соответствующие [[грань|грани]] имеют общее [[ребро]]. (Абстрактно) двойственный граф — это граф, у которого подмножество | ||
для данного плоского графа (геометрически) двойственный граф есть | ребер образует [[простой цикл]] тогда и только тогда, когда соответствующее ему (при некоторой биекции) подмножество ребер исходного графа образует [[простой разрез]] и наоборот. Справедливо | ||
снова плоский граф, вершины которого суть грани исходного графа и две | утверждение: граф, [[геометрически двойственный граф|геометрически двойственный]] плоскому графу, является абстрактно двойственным ему. | ||
вершины смежны, если соответствующие грани имеют общее ребро. | |||
(Абстрактно) двойственный граф | [[Файл:Dual graph.png|700px]] | ||
ребер образует простой цикл тогда и только тогда, когда | |||
соответствующее ему (при некоторой биекции) подмножество ребер | |||
исходного графа образует простой разрез и наоборот. Справедливо | |||
утверждение: граф, геометрически двойственный плоскому графу, | |||
является абстрактно двойственным ему. | |||
==Литература== | ==Литература== | ||
* Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990. | |||
Текущая версия от 05:57, 3 февраля 2011
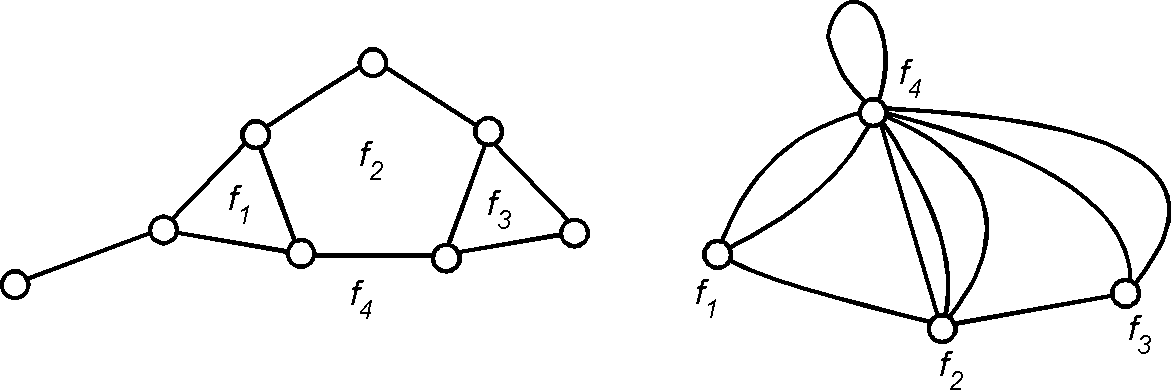
Двойственный граф (Dual graph) — для данного плоского графа (геометрически) двойственный граф есть снова плоский граф, вершины которого суть грани исходного графа и две вершины смежны, если соответствующие грани имеют общее ребро. (Абстрактно) двойственный граф — это граф, у которого подмножество ребер образует простой цикл тогда и только тогда, когда соответствующее ему (при некоторой биекции) подмножество ребер исходного графа образует простой разрез и наоборот. Справедливо утверждение: граф, геометрически двойственный плоскому графу, является абстрактно двойственным ему.
Литература
- Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.