Глубинное остовное дерево: различия между версиями
Перейти к навигации
Перейти к поиску
KEV (обсуждение | вклад) Нет описания правки |
KEV (обсуждение | вклад) Нет описания правки |
||
| (не показаны 4 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Глубинное остовное дерево''' (''[[Depth-first spanning tree]]'') | [[Файл:Depth-first spanning tree.png|350px|right]] | ||
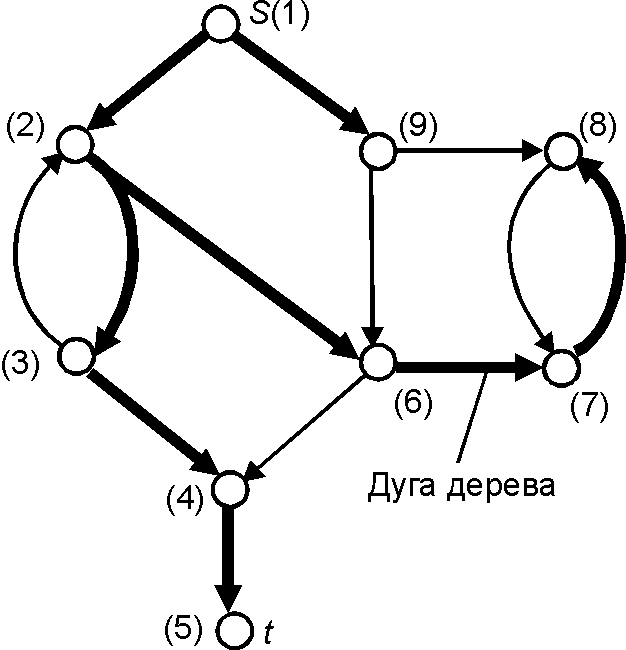
на четыре класса: [[древесная дуга|''древесные'' | '''Глубинное остовное дерево''' (''[[Depth-first spanning tree]]'') — '''1.''' Оркаркас в виде растущего [[ордерево|ордерева]], образованный [[древесная дуга|древесными дугами]] при реализации [[поиск в глубину|поиска в глубину]] в [[орграф|орграфе]]; [[корень]] ордерева совпадает с началом поиска в глубину. Все множество [[дуга|дуг]] орграфа разбивается относительно его '''глубинного остовного дерева''' | ||
на четыре класса: [[древесная дуга|''древесные'' — дуги]], принадлежащие [[дерево|дереву]]; [[обратная дуга|''обратные'' — дуги]], ведущие от [[потомок вершины|потомков]] к [[предок вершины|предкам]] (возможно, от вершин в себя); [[прямая дуга|''прямые'' — дуги]], идущие от предков к потомкам, но не являющиеся древесными; [[поперечная дуга|''поперечные'' — дуги]], соединяющие вершины, которые не являются ни предками, ни потомками относительно друг друга. | |||
'''2.''' [[Каркас]], построенный поиском в глубину в неориентированном [[граф|графе]]. | '''2.''' [[Каркас]], построенный поиском в глубину в неориентированном [[граф|графе]]. | ||
==Литература== | ==Литература== | ||
* Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985. | |||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
* Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990. | |||
Текущая версия от 09:34, 10 декабря 2010
Глубинное остовное дерево (Depth-first spanning tree) — 1. Оркаркас в виде растущего ордерева, образованный древесными дугами при реализации поиска в глубину в орграфе; корень ордерева совпадает с началом поиска в глубину. Все множество дуг орграфа разбивается относительно его глубинного остовного дерева на четыре класса: древесные — дуги, принадлежащие дереву; обратные — дуги, ведущие от потомков к предкам (возможно, от вершин в себя); прямые — дуги, идущие от предков к потомкам, но не являющиеся древесными; поперечные — дуги, соединяющие вершины, которые не являются ни предками, ни потомками относительно друг друга. 2. Каркас, построенный поиском в глубину в неориентированном графе.
Литература
- Евстигнеев В.А. Применение теории графов в программировании. — М.: Наука, 1985.
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.
- Лекции по теории графов / В.А.Емеличев, О.И.Мельников, В.И.Сарванов, Р.И.Тышкевич. — М.: Наука, 1990.