Матрица достижимости: различия между версиями
Перейти к навигации
Перейти к поиску
Glk (обсуждение | вклад) (Создана новая страница размером '''Матрица достижимости''' (''Reachability matrix'') - квадратная (0,1)-матрица <math>R(G)</math> р...) |
KEV (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
'''Матрица достижимости''' (''Reachability matrix'') - | '''Матрица достижимости''' (''[[Reachability matrix]]'') - | ||
квадратная (0,1)-матрица <math>R(G)</math> размером <math>n \times n</math> (<math>n</math> | квадратная (0,1)-матрица <math>R(G)</math> размером <math>n \times n</math> (<math>n</math> | ||
--- число вершин в <math>G</math>), <math>(i,j)</math>-й элемент <math>r_{ij}</math> которой | --- число [[вершина|вершин]] в <math>G</math>), <math>(i,j)</math>-й элемент <math>r_{ij}</math> которой | ||
равен 1, если в <math>G</math> существует путь из <math>v_{i}</math> в <math>v_{j}</math> | равен 1, если в <math>G</math> существует [[путь]] из <math>v_{i}</math> в <math>v_{j}</math> | ||
(вершина <math>v_{j}</math> достижима из <math>v_{i}</math>, и равен 0 в | (вершина <math>v_{j}</math> [[достижимая вершина|достижима]] из <math>v_{i}</math>, и равен 0 в | ||
противном случае. | противном случае. | ||
См. ''Транзитивное замыкание.'' | [[Файл:Reachability matrix.png]] | ||
==См.== | |||
''[[Транзитивное замыкание]].'' | |||
==Литература== | ==Литература== | ||
[Харари], | [Харари], | ||
[Евстигнеев/85] | [Евстигнеев/85] | ||
Версия от 05:44, 23 ноября 2009
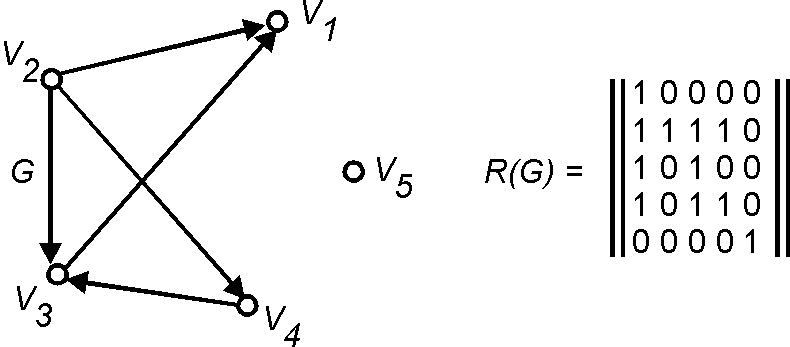
Матрица достижимости (Reachability matrix) - квадратная (0,1)-матрица [math]\displaystyle{ R(G) }[/math] размером [math]\displaystyle{ n \times n }[/math] ([math]\displaystyle{ n }[/math] --- число вершин в [math]\displaystyle{ G }[/math]), [math]\displaystyle{ (i,j) }[/math]-й элемент [math]\displaystyle{ r_{ij} }[/math] которой равен 1, если в [math]\displaystyle{ G }[/math] существует путь из [math]\displaystyle{ v_{i} }[/math] в [math]\displaystyle{ v_{j} }[/math] (вершина [math]\displaystyle{ v_{j} }[/math] достижима из [math]\displaystyle{ v_{i} }[/math], и равен 0 в противном случае.
См.
Литература
[Харари],
[Евстигнеев/85]