Автомат с магазинной памятью

Автомат с магазинной памятью (Pushdown automaton) — тип абстрактной машины, определяющий класс контекстно-свободных языков.

Автомат с магазинной памятью (сокращенно МП-автомат ) — это семерка $P=(Q,\mathrm{\Sigma },\mathrm{\Gamma },\delta ,q_0,Z_0,F)$, где

(1) $Q$ — конечное множество символов состояний, представляющих возможные состояния управляющего устройства;

(2) $\mathrm{\Sigma }$ — конечный входной алфавит;

(3) $\mathrm{\Gamma }$ — конечный алфавит магазинных символов;

(4) $\delta$ — отображение множества $Q\times (\mathrm{\Sigma }\cup \{e\})\times \mathrm{\Gamma }$ в множество конечных подмножеств множества $Q\times {\mathrm{\Gamma }}^{\ast }$;

(5) $q_0\in Q$ — начальное состояние управляющего устройства;

(6) $Z_0\in \mathrm{\Gamma }$ — символ, находящийся в магазине в начальный момент (начальный символ);

(7) $F\subseteq Q$ — множество заключительных состояний.

Конфигурацией МП-автомата $P$ называется тройка $(q,\omega ,\alpha )\in Q\times {\mathrm{\Sigma }}^{\ast }\times {\mathrm{\Gamma }}^{\ast }$, где

(1) $q$ — текущее состояние управляющего устройства;

(2) $\omega$ — неиспользованная часть входной цепочки; первый символ цепочки $\omega$ находится под входной головкой; если $\omega =e$, то считается, что вся входная лента прочитана;

(3) $\alpha$ — содержимое магазина; самый левый символ цепочки считается верхним символом магазина; если $\alpha =e$, то магазин считается пустым.

Начальной конфигурацией МП-автомата $P$ называется конфигурация вида $(q_0,\omega ,Z_0)$, где $\omega \in {\mathrm{\Sigma }}^{\ast }$. Заключительная его конфигурация — это конфигурация вида $(q,e,e)$, где $q\in F$.

Такт работы МП-автомата $P$ представляется в виде бинарного отношения ${⊢}_P$, определенного на конфигурациях следующим образом: $(q,$ $a\omega ,$ $Z\alpha ){⊢}_P(p,\omega ,\gamma \alpha )$, если множество $\delta (q,a,Z)$ содержит $(p,\gamma )$, где $q,p\in Q,$ $a\in \mathrm{\Sigma }\cup \{e\},$ $\omega \in {\mathrm{\Sigma }}^{\ast },$ $Z\in \mathrm{\Gamma }$ и $\alpha ,\gamma \in {\mathrm{\Gamma }}^{\ast }$. Через ${⊢}_P^{\ast }$ и ${⊢}_P^{+}$ обозначаются соответственно рефлексивное и транзитивное замыкание и транзитивное замыкание отношения ${⊢}_P$.

Цепочка $\omega$ допускается МП-автоматом $P$, если $(q_0,\omega ,Z_0){⊢}_P^{\ast }(q,e,e)$ для некоторого $q\in F$.

Языком, определяемым (или допускаемым) автоматом $P$ (обозначается $L(P)$), называют множество цепочек, допускаемых автоматом $P$.

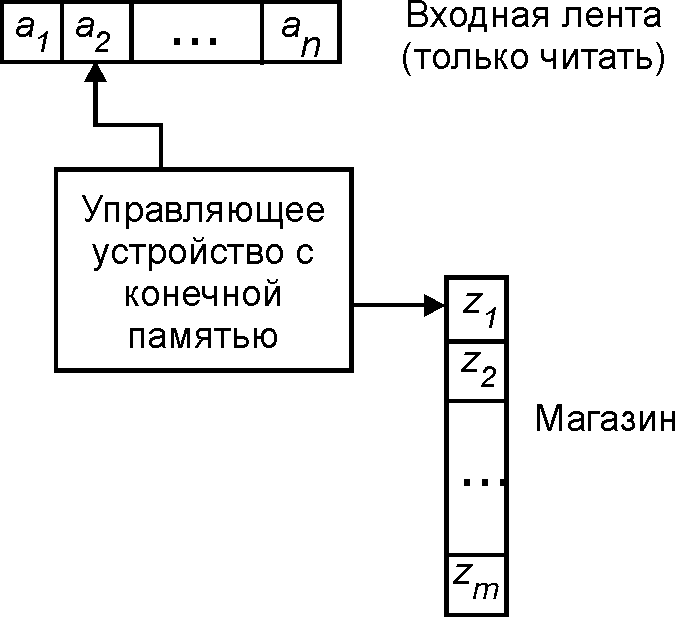
Сравнивая понятия конечного и магазинного автоматов, можно сказать, что МП-автомат получается из конечного автомата добавлением потенциально бесконечной рабочей (вспомогательной) памяти, в которой элементы информации хранятся и используются так же как патроны в магазине автоматического оружия, т.е. в каждый момент доступен только верхний элемент магазина.

Такт работы некоторого МП-автомата $P$, связанный с переходом от конфигурации $(q,a\omega ,Za)$ к конфигурации $(q^{\prime },\omega ,\gamma a)$ при $a\ne e$, говорит о том, что МП-автомат $P$, находясь в состоянии $q$ и имея $a$ в качестве текущего входного символа, расположенного под входной головкой (т.е. обозревая $a$), а $Z$ — в качестве верхнего символа магазина, может перейти в новое состояние $q^{\prime }$, сдвинуть входную головку на одну ячейку вправо и заменить верхний символ магазина цепочкой $\gamma$ магазинных символов. Если $\gamma =e$, то верхний символ удаляется из магазина и, тем самым, магазинный список сокращается.

Такт, в котором $a=e$, называют е-тактом. В $e$-такте текущий входной символ не принимается во внимание и входная головка не сдвигается. Однако состояние управляющего устройства и содержимое памяти могут измениться. Заметим, что $e$-такт может происходить и тогда, когда вся входная цепочка прочитана.

Литература

• Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. — М.: Мир, 1979.
• Касьянов В.Н. Лекции по теории формальных языков, автоматов и сложности вычислений. — Новосибирск: НГУ, 1995.
• Касьянов В.Н., Касьянова Е.В. Теория вычислений. — Новосибирск: НГУ, 2018.
• Касьянов В.Н., Поттосин И.В. Методы построения трансляторов. — Новосибирск: Наука. Сиб. отд-ние, 1986.