Каркас уграфа: различия между версиями
KVN (обсуждение | вклад) |
KVN (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
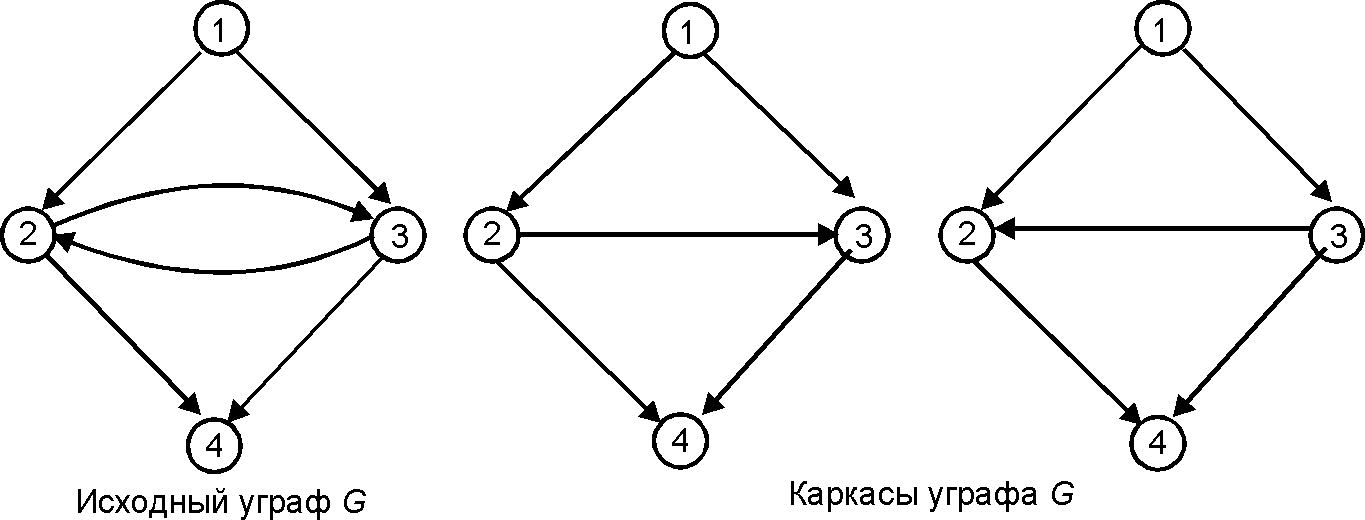
'''Каркас уграфа''' (''[[Spanner of control flow graph]], [[Dag of control flow graph|DAG of control flow graph]]'') — такой ''[[уграф]]'' <math>K</math>, что <math>K</math> — ''[[Ациклический граф|ациклический]] [[остов]]'' уграфа <math>G</math>, | '''Каркас уграфа''' (''[[Spanner of control flow graph]], [[Dag of control flow graph|DAG of control flow graph]]'') — такой ''[[уграф]]'' <math>K</math>, что <math>K</math> — ''[[Ациклический граф|ациклический]] [[остов]]'' уграфа <math>G</math>, '''каркасом''' которого он является, и добавление в <math>K</math> еще одной любой [[дуга|дуги]] <math>G</math> нарушает ацикличность <math>K</math>. | ||
[[Файл:DAG of control flow graph.png|700px]] | [[Файл:DAG of control flow graph.png|700px]] | ||
Текущая версия от 10:09, 18 ноября 2024
Каркас уграфа (Spanner of control flow graph, DAG of control flow graph) — такой уграф [math]\displaystyle{ K }[/math], что [math]\displaystyle{ K }[/math] — ациклический остов уграфа [math]\displaystyle{ G }[/math], каркасом которого он является, и добавление в [math]\displaystyle{ K }[/math] еще одной любой дуги [math]\displaystyle{ G }[/math] нарушает ацикличность [math]\displaystyle{ K }[/math].
Справедливы следующие свойства:
(1) Для любого простого пути [math]\displaystyle{ P }[/math] по [math]\displaystyle{ G }[/math] от ее начальной вершины [math]\displaystyle{ p_0 }[/math] существует такой каркас [math]\displaystyle{ K }[/math] уграфа [math]\displaystyle{ G }[/math], что [math]\displaystyle{ P }[/math] является путем по [math]\displaystyle{ K }[/math].
(2) Каркас любого аранжируемого уграфа [math]\displaystyle{ G }[/math] может быть получен из [math]\displaystyle{ G }[/math] удалением всех дуг назад.
(3) Уграф [math]\displaystyle{ G }[/math] является регуляризуемым тогда и только тогда, когда имеет единственный каркас.
(4) Уграф [math]\displaystyle{ G }[/math] является регуляризуемым тогда и только тогда, когда существует такое разбиение множества его дуг [math]\displaystyle{ U }[/math] на два подмножества [math]\displaystyle{ U_1 }[/math] и [math]\displaystyle{ U_2 }[/math], что [math]\displaystyle{ U_1 }[/math] образует каркас уграфа, а для любой дуги [math]\displaystyle{ (p, q)\in U_2 }[/math] вершина [math]\displaystyle{ q }[/math] обязательно предшествует вершине [math]\displaystyle{ p }[/math] в [math]\displaystyle{ G }[/math].
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.
- Касьянов В.Н., Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение. — СПб.: БХВ-Петербург, 2003.