Фрагмент уграфа: различия между версиями
KEV (обсуждение | вклад) Нет описания правки |
KVN (обсуждение | вклад) Нет описания правки |
||
| (не показаны 3 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
'''Фрагмент''' (''[[Fragment]]'') | '''Фрагмент уграфа''' (''[[Fragment of flow graph]]'') — любая часть [[уграф|уграфа]]. Фрагмент <math>C</math> является ''[[подфрагмент|подфрагментом]]'' фрагмента <math>S</math>, если <math>C</math> — часть <math>S</math>. | ||
любая часть [[уграф|уграфа]]. Фрагмент <math>C</math> является | |||
''[[подфрагмент|подфрагментом]]'' фрагмента <math>S</math>, если <math>C</math> | |||
Подфрагмент <math>C</math> фрагмента <math>S</math>, отличный от <math>S</math>, называется | Подфрагмент <math>C</math> фрагмента <math>S</math>, отличный от <math>S</math>, называется | ||
[[собственный подфрагмент|''собственным'' подфрагментом]]. | [[собственный подфрагмент|''собственным'' подфрагментом]]. | ||
[[Вершина]] <math>p</math> фрагмента <math>C</math> называется ''[[начальная вершина|начальной]]'' | [[Вершина]] <math>p</math> фрагмента <math>C</math> называется ''[[начальная вершина|начальной]]'' | ||
(соответственно ''[[выходная вершина фрагмента|выходной]]''), если либо <math>p</math> | (соответственно ''[[выходная вершина фрагмента|выходной]]''), если либо <math>p</math> — начальная | ||
(соответственно [[конечная вершина|конечная]]) вершина уграфа, либо в <math>p</math> заходит | (соответственно [[конечная вершина|конечная]]) вершина уграфа, либо в <math>p</math> заходит | ||
(соответственно из <math>p</math> исходит) [[дуга]] уграфа, не | (соответственно из <math>p</math> исходит) [[дуга]] уграфа, не | ||
| Строка 30: | Строка 28: | ||
Фрагмент называется ''[[правильный фрагмент|правильным]]'', если он имеет в точности две | Фрагмент называется ''[[правильный фрагмент|правильным]]'', если он имеет в точности две | ||
граничные вершины, одна из которых | граничные вершины, одна из которых — стартовая, а вторая — | ||
финишная. Правильный фрагмент называется ''[[простой фрагмент|простым]]'', если он | финишная. Правильный фрагмент называется ''[[простой фрагмент|простым]]'', если он | ||
содержит одну дугу. | содержит одну дугу. | ||
| Строка 39: | Строка 37: | ||
==См. также == | ==См. также == | ||
''[[Альт]], [[Гамак]], [[Зона]], [[Интервал]], [[Линейная компонента]], [[Линейный участок]], [[Луч]].'' | * ''[[Альт]],'' | ||
* ''[[Гамак]],'' | |||
* ''[[Зона]],'' | |||
* ''[[Интервал]],'' | |||
* ''[[Линейная компонента]],'' | |||
* ''[[Линейный участок]],'' | |||
* ''[[Луч]].'' | |||
==Литература== | ==Литература== | ||
* Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994. | |||
* Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988. | |||
* Касьянов В. Н., Евстигнеев В. А. Графы в программировании: обработка, визуализация и применение. – СПб.: БХВ-Петербург, 2003. – 1104 c. | |||
[ | |||
[[Категория: Потоковый анализ программ]] | |||
Текущая версия от 13:14, 4 ноября 2024
Фрагмент уграфа (Fragment of flow graph) — любая часть уграфа. Фрагмент [math]\displaystyle{ C }[/math] является подфрагментом фрагмента [math]\displaystyle{ S }[/math], если [math]\displaystyle{ C }[/math] — часть [math]\displaystyle{ S }[/math]. Подфрагмент [math]\displaystyle{ C }[/math] фрагмента [math]\displaystyle{ S }[/math], отличный от [math]\displaystyle{ S }[/math], называется собственным подфрагментом.
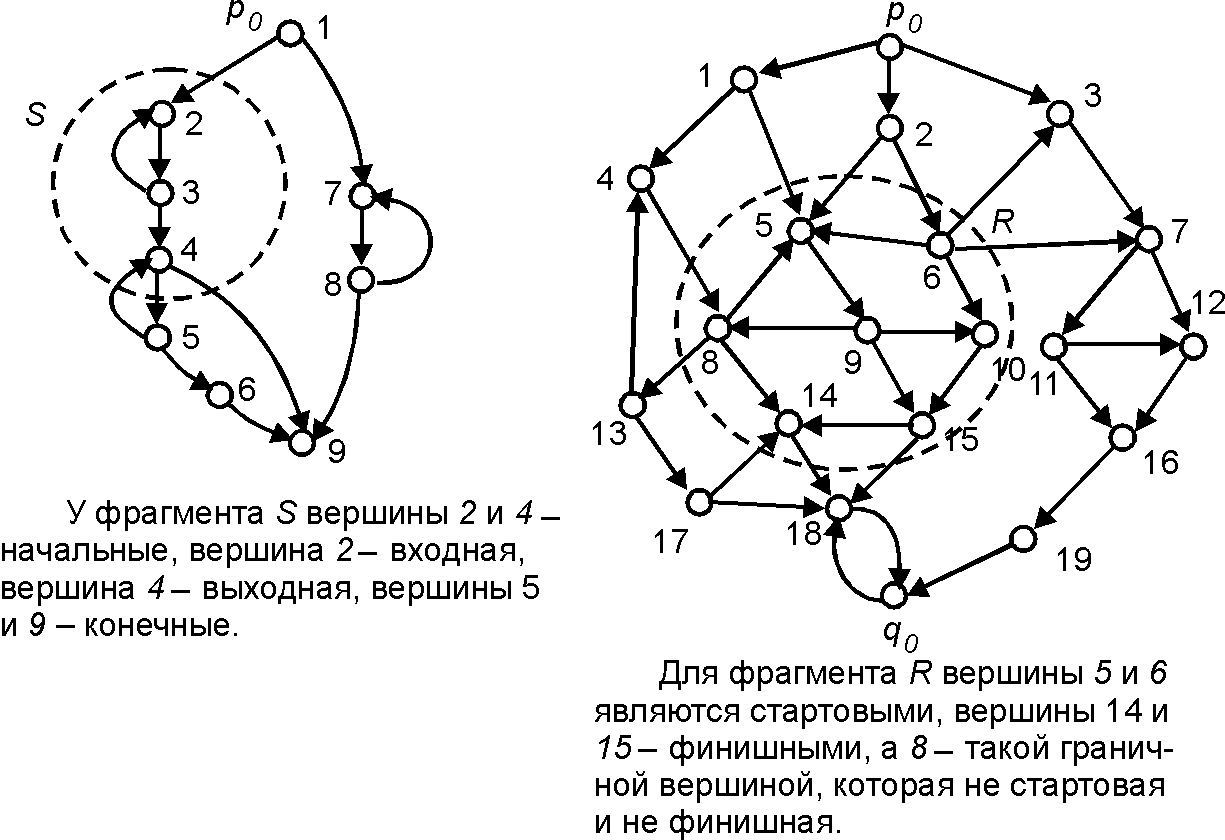
Вершина [math]\displaystyle{ p }[/math] фрагмента [math]\displaystyle{ C }[/math] называется начальной (соответственно выходной), если либо [math]\displaystyle{ p }[/math] — начальная (соответственно конечная) вершина уграфа, либо в [math]\displaystyle{ p }[/math] заходит (соответственно из [math]\displaystyle{ p }[/math] исходит) дуга уграфа, не принадлежащая [math]\displaystyle{ C }[/math]. Вершина [math]\displaystyle{ p }[/math] фрагмента [math]\displaystyle{ C }[/math] называется входной (или входом), если существует путь по уграфу от его начальной вершины до [math]\displaystyle{ p }[/math], не содержащий дуг [math]\displaystyle{ C }[/math]. Вершина [math]\displaystyle{ p }[/math] называется конечной для фрагмента [math]\displaystyle{ C }[/math], если она не принадлежит [math]\displaystyle{ C }[/math] и является преемником хотя бы одной его вершины.
Вершина [math]\displaystyle{ p }[/math] фрагмента [math]\displaystyle{ C }[/math], отличная от начальной и конечной вершин уграфа, называется граничной вершиной [math]\displaystyle{ C }[/math], если [math]\displaystyle{ p }[/math] является начальной или выходной вершиной [math]\displaystyle{ C }[/math]. Граничная вершина [math]\displaystyle{ p }[/math] фрагмента [math]\displaystyle{ C }[/math] называется стартовой, если в нее не заходят дуги фрагмента [math]\displaystyle{ C }[/math] или из нее не исходят дуги, не принадлежащие [math]\displaystyle{ C }[/math], и финишной, если в нее заходят лишь дуги фрагмента [math]\displaystyle{ C }[/math] или из нее не исходят дуги, принадлежащие [math]\displaystyle{ C }[/math].
Фрагмент называется правильным, если он имеет в точности две
граничные вершины, одна из которых — стартовая, а вторая —
финишная. Правильный фрагмент называется простым, если он
содержит одну дугу.
Правильный фрагмент, не являющийся простым, называется первичным, если все его собственные правильные подфрагменты являются простыми.
См. также
Литература
- Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
- Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.
- Касьянов В. Н., Евстигнеев В. А. Графы в программировании: обработка, визуализация и применение. – СПб.: БХВ-Петербург, 2003. – 1104 c.