Фрагмент уграфа

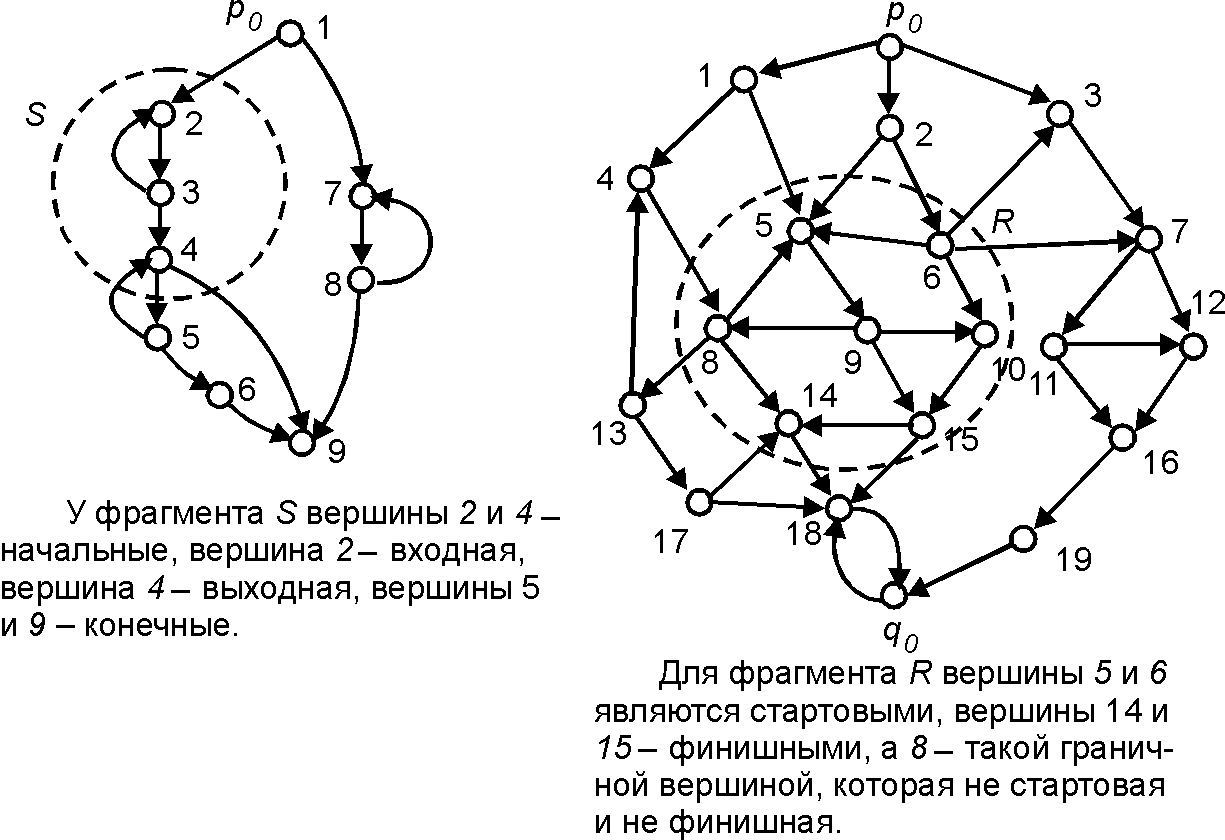
Фрагмент (Fragment) — любая часть уграфа. Фрагмент [math]\displaystyle{ C }[/math] является подфрагментом фрагмента [math]\displaystyle{ S }[/math], если [math]\displaystyle{ C }[/math] — часть [math]\displaystyle{ S }[/math]. Подфрагмент [math]\displaystyle{ C }[/math] фрагмента [math]\displaystyle{ S }[/math], отличный от [math]\displaystyle{ S }[/math], называется собственным подфрагментом.

Вершина [math]\displaystyle{ p }[/math] фрагмента [math]\displaystyle{ C }[/math] называется начальной (соответственно выходной), если либо [math]\displaystyle{ p }[/math] — начальная (соответственно конечная) вершина уграфа, либо в [math]\displaystyle{ p }[/math] заходит (соответственно из [math]\displaystyle{ p }[/math] исходит) дуга уграфа, не принадлежащая [math]\displaystyle{ C }[/math]. Вершина [math]\displaystyle{ p }[/math] фрагмента [math]\displaystyle{ C }[/math] называется входной (или входом), если существует путь по уграфу от его начальной вершины до [math]\displaystyle{ p }[/math], не содержащий дуг [math]\displaystyle{ C }[/math]. Вершина [math]\displaystyle{ p }[/math] называется конечной для фрагмента [math]\displaystyle{ C }[/math], если она не принадлежит [math]\displaystyle{ C }[/math] и является преемником хотя бы одной его вершины.

Вершина [math]\displaystyle{ p }[/math] фрагмента [math]\displaystyle{ C }[/math], отличная от начальной и конечной вершин уграфа, называется граничной вершиной [math]\displaystyle{ C }[/math], если [math]\displaystyle{ p }[/math] является начальной или выходной вершиной [math]\displaystyle{ C }[/math]. Граничная вершина [math]\displaystyle{ p }[/math] фрагмента [math]\displaystyle{ C }[/math] называется стартовой, если в нее не заходят дуги фрагмента [math]\displaystyle{ C }[/math] или из нее не исходят дуги, не принадлежащие [math]\displaystyle{ C }[/math], и финишной, если в нее заходят лишь дуги фрагмента [math]\displaystyle{ C }[/math] или из нее не исходят дуги, принадлежащие [math]\displaystyle{ C }[/math].

Фрагмент называется правильным, если он имеет в точности две граничные вершины, одна из которых — стартовая, а вторая — финишная. Правильный фрагмент называется простым, если он содержит одну дугу.

Правильный фрагмент, не являющийся простым, называется первичным, если все его собственные правильные подфрагменты являются простыми.

См. также

• Альт,
• Гамак,
• Зона,
• Интервал,
• Линейная компонента,
• Линейный участок,
• Луч.

Литература

• Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука. Сиб. отд-ние, 1994.
• Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.
• Касьянов В. Н., Евстигнеев В. А. Графы в программировании: обработка, визуализация и применение. – СПб.: БХВ-Петербург, 2003. – 1104 c.