Семантическая сеть: различия между версиями
KEV (обсуждение | вклад) Нет описания правки |
Tanya (обсуждение | вклад) Нет описания правки |
||
| (не показаны 3 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
'''Семантическая сеть''' (''[[Semantic | '''Семантическая сеть''' (''[[Semantic net]]'') — | ||
средство для представления знаний в виде [[помеченный | средство для представления знаний в виде [[помеченный граф|помеченного орграфа]]. Каждая | ||
[[вершина]] этого [[граф|графа]] представляет собой понятие, или концепт, а каждая | [[вершина]] этого [[граф|графа]] представляет собой понятие, или концепт, а каждая | ||
[[метка]] представляет связь между концептами. При выполнении процедур, | [[метка]] представляет связь между концептами. При выполнении процедур, | ||
| Строка 6: | Строка 6: | ||
связей между ними, производится движение по этому графу и его | связей между ними, производится движение по этому графу и его | ||
обработка. | обработка. | ||
'''Семантическая сеть''' (''[[Semantic network]]'') — информационная модель предметной области, имеющая вид [[Ориентированный граф|ориентированного графа]], [[вершина|вершины]] которого соответствуют объектам предметной области, а [[дуга|дуги]] (рёбра) задают отношения между ними. Объектами могут быть понятия, события, свойства, процессы. Таким образом, семантическая сеть является одним из способов представления знаний. В названии соединены термины из двух наук: семантика в языкознании изучает смысл единиц языка, а сеть в математике представляет собой разновидность [[граф|графа]] — набора вершин, соединённых дугами (рёбрами), которым присвоено некоторое число. В семантической сети роль вершин выполняют понятия базы знаний, а дуги (причем направленные) задают отношения между ними. Таким образом, семантическая сеть отражает семантику предметной области в виде понятий и отношений. | |||
'''История''' | |||
Идея систематизации на основе каких-либо семантических отношений предлагалась ещё учёными ранней науки. Примером этого может служить биологическая классификация Карла Линнея 1735 г. Если рассматривать её как семантическую сеть, то в данной классификации используется отношение подмножества, современное AKO (от англ. «A Kind Of», «разновидность»). | |||
Прародителями современных семантических сетей можно считать [[экзистенциальный_граф|экзистенциальные графы]], предложенные Чарльзом Пирсом в 1909 г. Они использовались для представления логических высказываний в виде особых диаграмм. Пирс назвал этот способ «логикой будущего». | |||
Важным направлением в исследовании сетей стали работы немецкого психолога Отто Зельца 1913 и 1922 гг. В них для организации структур понятий и ассоциаций, а также изучения методов наследования свойств он использовал графы и семантические отношения. Исследователи Дж. Андерсон (1973), Д. Норман (1975) и другие использовали эти работы для моделирования человеческой памяти и интеллектуальных свойств. | |||
Компьютерные семантические сети были детально разработаны Ричардом Риченсом (англ.) в 1956 году в рамках проекта Кембриджского центра изучения языка по машинному переводу. Процесс машинного перевода подразделяется на 2 части: перевод исходного текста в промежуточную форму представления, а затем эта промежуточная форма транслируется на нужный язык. Такой промежуточной формой как раз и были семантические сети. В 1961 г. появилась работа Мастерман (англ.), в которой она, в частности, определяла базовый словарь для 15000 понятий. Эти исследования были продолжены Робертом Симмонсом (1966), Й. Уилксом (1972) и другими учёными. | |||
Труды по семантическим сетям часто ссылаются на работу американского психолога Росса Квиллиана (Quillian) о «семантической памяти». | |||
'''Структура''' | |||
Математика позволяет описать большинство явлений в окружающем мире в виде логических высказываний. Семантические сети возникли как попытка визуализации математических формул. Основным представлением для семантической сети является [[граф]]. Однако не стоит забывать, что за графическим изображением непременно стоит строгая математическая запись, и что обе эти формы отображают одно и то же. | |||
''Графическое представление'' | |||
Основной формой представления семантической сети является [[граф]]. Понятия семантической сети записываются в овалах или прямоугольниках и соединяются стрелками с подписями — дугами. Это наиболее удобно воспринимаемая человеком форма. Её недостатки проявляются, когда мы начинаем строить более сложные сети или пытаемся учесть особенности естественного языка. Схемы семантических сетей, на которых указаны направления навигационных отношений, называют картами знаний, а их совокупность, позволяющая охватить большие участки семантической сети, атласом знания. | |||
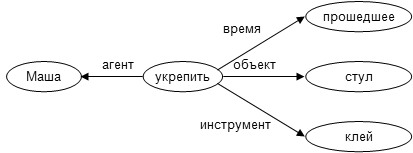
[[Файл:Semantic_net.png]] | |||
''Пример семантической сети: «Маша укрепила стул клеем»'' | |||
''Математическая запись'' | |||
В математике [[граф]] представляется множеством [[вершина|вершин]] V и множеством отношений между ними E. Используя аппарат математической логики, приходим к выводу, что каждая вершина соответствует элементу предметного множества, а [[дуга]] — предикату. | |||
''Лингвистическая запись'' | |||
В лингвистике отношения фиксируются в словарях и в тезаурусах. В словарях в определениях через род и видовое отличие родовое понятие занимает определённое место. В тезаурусах в статье каждого термина могут быть указаны все возможные его связи с другими родственными по теме терминами. От таких тезаурусов необходимо отличать тезаурусы информационно-поисковые с перечнями ключевых слов в статьях, которые предназначены для работы дескрипторных поисковых систем. | |||
'''Классификация семантических сетей''' | |||
Для всех семантических сетей справедливо разделение по арности и количеству типов отношений. | |||
По ''количеству типов отношений'', сети могут быть однородными и неоднородными. ''Однородные сети'' обладают только одним типом отношений (стрелок), например, таковой является вышеупомянутая классификация биологических видов (с единственным отношением AKO). | |||
В ''неоднородных сетях'' количество типов отношений больше одного. Классические иллюстрации данной модели представления знаний представляют именно такие сети. Неоднородные сети представляют больший интерес для практических целей, но и большую сложность для исследования. Неоднородные сети можно представлять как переплетение древовидных многослойных структур. Примером такой сети может быть Семантическая сеть Википедии. | |||
По ''арности'': типичными являются сети с бинарными отношениями (связывающими ровно два понятия). Бинарные отношения очень просты и удобно изображаются на графе в виде стрелки между двух концептов. Кроме того, они играют исключительную роль в математике. | |||
На практике, однако, могут понадобиться отношения, связывающие более двух объектов — N-арные. При этом возникает сложность — как изобразить подобную связь на графе, чтобы не запутаться. [[концептуальный граф|Концептуальные графы]] (см. ниже) снимают это затруднение, представляя каждое отношение в виде отдельного узла. | |||
По ''размеру'': Для решения конкретных задач, например, тех которые решают системы искусственного интеллекта. | |||
Семантическая сеть отраслевого масштаба должна служить базой для создания конкретных систем, не претендуя на всеобщее значение. | |||
Глобальная семантическая сеть. Теоретически такая сеть должна существовать, поскольку всё в мире взаимосвязано. Возможно когда-нибудь такой сетью станет Всемирная паутина. | |||
Помимо [[концептуальный граф|концептуальных графов]] существуют и другие модификации семантических сетей, это является ещё одной основой для классификации (по реализации). | |||
==Литература== | ==Литература== | ||
* John F. Sowa (1987). "Semantic Networks". In Stuart C Shapiro. Encyclopedia of Artificial Intelligence. | |||
* Allen, J. and A. Frisch (1982). "What's in a Semantic Network". In: Proceedings of the 20th. annual meeting of ACL, Toronto, pp. 19–27. | |||
* John F. Sowa, Alexander Borgida (1991). Principles of Semantic Networks: Explorations in the Representation of Knowledge. | |||
* Lehmann, Fritz, ed. (1992) Semantic Networks in Artificial Intelligence, Oxford: Pergamon Press. Also published as a special issue of Computers and Mathematics with Applications 23:6-9. | |||
* Толковый словарь по вычислительным системам. — М.: Машиностроение, 1991. | |||
Текущая версия от 04:42, 2 августа 2016
Семантическая сеть (Semantic net) — средство для представления знаний в виде помеченного орграфа. Каждая вершина этого графа представляет собой понятие, или концепт, а каждая метка представляет связь между концептами. При выполнении процедур, связанных с доступом к концептам, а также изменением самих концептов и связей между ними, производится движение по этому графу и его обработка.
Семантическая сеть (Semantic network) — информационная модель предметной области, имеющая вид ориентированного графа, вершины которого соответствуют объектам предметной области, а дуги (рёбра) задают отношения между ними. Объектами могут быть понятия, события, свойства, процессы. Таким образом, семантическая сеть является одним из способов представления знаний. В названии соединены термины из двух наук: семантика в языкознании изучает смысл единиц языка, а сеть в математике представляет собой разновидность графа — набора вершин, соединённых дугами (рёбрами), которым присвоено некоторое число. В семантической сети роль вершин выполняют понятия базы знаний, а дуги (причем направленные) задают отношения между ними. Таким образом, семантическая сеть отражает семантику предметной области в виде понятий и отношений.
История
Идея систематизации на основе каких-либо семантических отношений предлагалась ещё учёными ранней науки. Примером этого может служить биологическая классификация Карла Линнея 1735 г. Если рассматривать её как семантическую сеть, то в данной классификации используется отношение подмножества, современное AKO (от англ. «A Kind Of», «разновидность»).
Прародителями современных семантических сетей можно считать экзистенциальные графы, предложенные Чарльзом Пирсом в 1909 г. Они использовались для представления логических высказываний в виде особых диаграмм. Пирс назвал этот способ «логикой будущего».
Важным направлением в исследовании сетей стали работы немецкого психолога Отто Зельца 1913 и 1922 гг. В них для организации структур понятий и ассоциаций, а также изучения методов наследования свойств он использовал графы и семантические отношения. Исследователи Дж. Андерсон (1973), Д. Норман (1975) и другие использовали эти работы для моделирования человеческой памяти и интеллектуальных свойств.
Компьютерные семантические сети были детально разработаны Ричардом Риченсом (англ.) в 1956 году в рамках проекта Кембриджского центра изучения языка по машинному переводу. Процесс машинного перевода подразделяется на 2 части: перевод исходного текста в промежуточную форму представления, а затем эта промежуточная форма транслируется на нужный язык. Такой промежуточной формой как раз и были семантические сети. В 1961 г. появилась работа Мастерман (англ.), в которой она, в частности, определяла базовый словарь для 15000 понятий. Эти исследования были продолжены Робертом Симмонсом (1966), Й. Уилксом (1972) и другими учёными.
Труды по семантическим сетям часто ссылаются на работу американского психолога Росса Квиллиана (Quillian) о «семантической памяти».
Структура
Математика позволяет описать большинство явлений в окружающем мире в виде логических высказываний. Семантические сети возникли как попытка визуализации математических формул. Основным представлением для семантической сети является граф. Однако не стоит забывать, что за графическим изображением непременно стоит строгая математическая запись, и что обе эти формы отображают одно и то же.
Графическое представление
Основной формой представления семантической сети является граф. Понятия семантической сети записываются в овалах или прямоугольниках и соединяются стрелками с подписями — дугами. Это наиболее удобно воспринимаемая человеком форма. Её недостатки проявляются, когда мы начинаем строить более сложные сети или пытаемся учесть особенности естественного языка. Схемы семантических сетей, на которых указаны направления навигационных отношений, называют картами знаний, а их совокупность, позволяющая охватить большие участки семантической сети, атласом знания.
Пример семантической сети: «Маша укрепила стул клеем»
Математическая запись
В математике граф представляется множеством вершин V и множеством отношений между ними E. Используя аппарат математической логики, приходим к выводу, что каждая вершина соответствует элементу предметного множества, а дуга — предикату.
Лингвистическая запись
В лингвистике отношения фиксируются в словарях и в тезаурусах. В словарях в определениях через род и видовое отличие родовое понятие занимает определённое место. В тезаурусах в статье каждого термина могут быть указаны все возможные его связи с другими родственными по теме терминами. От таких тезаурусов необходимо отличать тезаурусы информационно-поисковые с перечнями ключевых слов в статьях, которые предназначены для работы дескрипторных поисковых систем.
Классификация семантических сетей
Для всех семантических сетей справедливо разделение по арности и количеству типов отношений.
По количеству типов отношений, сети могут быть однородными и неоднородными. Однородные сети обладают только одним типом отношений (стрелок), например, таковой является вышеупомянутая классификация биологических видов (с единственным отношением AKO). В неоднородных сетях количество типов отношений больше одного. Классические иллюстрации данной модели представления знаний представляют именно такие сети. Неоднородные сети представляют больший интерес для практических целей, но и большую сложность для исследования. Неоднородные сети можно представлять как переплетение древовидных многослойных структур. Примером такой сети может быть Семантическая сеть Википедии.
По арности: типичными являются сети с бинарными отношениями (связывающими ровно два понятия). Бинарные отношения очень просты и удобно изображаются на графе в виде стрелки между двух концептов. Кроме того, они играют исключительную роль в математике. На практике, однако, могут понадобиться отношения, связывающие более двух объектов — N-арные. При этом возникает сложность — как изобразить подобную связь на графе, чтобы не запутаться. Концептуальные графы (см. ниже) снимают это затруднение, представляя каждое отношение в виде отдельного узла.
По размеру: Для решения конкретных задач, например, тех которые решают системы искусственного интеллекта. Семантическая сеть отраслевого масштаба должна служить базой для создания конкретных систем, не претендуя на всеобщее значение. Глобальная семантическая сеть. Теоретически такая сеть должна существовать, поскольку всё в мире взаимосвязано. Возможно когда-нибудь такой сетью станет Всемирная паутина.
Помимо концептуальных графов существуют и другие модификации семантических сетей, это является ещё одной основой для классификации (по реализации).
Литература
- John F. Sowa (1987). "Semantic Networks". In Stuart C Shapiro. Encyclopedia of Artificial Intelligence.
- Allen, J. and A. Frisch (1982). "What's in a Semantic Network". In: Proceedings of the 20th. annual meeting of ACL, Toronto, pp. 19–27.
- John F. Sowa, Alexander Borgida (1991). Principles of Semantic Networks: Explorations in the Representation of Knowledge.
- Lehmann, Fritz, ed. (1992) Semantic Networks in Artificial Intelligence, Oxford: Pergamon Press. Also published as a special issue of Computers and Mathematics with Applications 23:6-9.
- Толковый словарь по вычислительным системам. — М.: Машиностроение, 1991.